CQOI2015终于全做完了~~~，讲一下题吧
首先这套题比起其他省选还是比较水的，就是5道题比较蛋疼
T1：[CQOI2015]选数
这道题还是比较神的。
首先给个比较神的题解：popoqqq大神的blog这个莫比乌斯反演真的不会
我们记f[i]为gcd=i*k时的个数，可以得到若数都不相等的话，i一定小于1e5（辗转相减法可得），那么当数都不相等时，答案显然为(r/(k*i)-l/(k*i)+1)^n-(r/(k*i)-l/(k*i)+1)-sigma(f[i*j])然后就能愉快的推出来啦，还有就是当l=1时要特判一下
CODE：
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 #define mod 1000000007 7 typedef long long ll; 8 int power(ll x,ll y) { 9 ll ans=1; 10 for (;y;y>>=1){ 11 if (y&1) (ans*=x)%=mod; 12 (x*=x)%=mod; 13 } 14 return ans; 15 } 16 ll n,l,k,h; 17 #define maxk 100000 18 ll f[maxk+10]; 19 int main(){ 20 freopen("number.in","r",stdin); 21 freopen("number.out","w",stdout); 22 ll L,H; 23 scanf("%lld%lld%lld%lld",&n,&k,&L,&H); 24 ll l=L/k,h=H/k; 25 if (L%k) l++; 26 int tmp=0; 27 for (int i=maxk;i;i--) { 28 ll L=l/i,H=h/i; 29 if (l%i) L++; 30 f[i]=(power(H-L+1,n)-(H-L+1)+mod)%mod; 31 for (int j=i+i;j<=maxk;j+=i) f[i]=(f[i]-f[j]+mod)%mod; 32 } 33 if (l==1) f[1]++; 34 printf("%lld ",f[1]); 35 return 0; 36 }
这不就是先求出最短路图后拆点跑个最大流么= =。直接做就行了不要考虑时间问题。。。
CODE：
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 using namespace std; 7 typedef long long ll; 8 #define maxm 150000 9 #define maxn 1100 10 struct edges{ 11 int to,next,dist;ll cap; 12 }edge[maxm*2]; 13 int l,next[maxn]; 14 inline void _addedge(int x,int y,int z){ 15 l++; 16 edge[l*2]=(edges) {x,next[y],z,0};next[y]=l*2; 17 edge[l*2+1]=(edges) {y,next[x],z,0};next[x]=l*2+1; 18 } 19 inline void addedge(int x,int y,ll z){ 20 l++; 21 edge[l*2]=(edges){y,next[x],0,z};next[x]=l*2; 22 edge[l*2+1]=(edges){x,next[y],0,0};next[y]=l*2+1; 23 } 24 ll dist[maxn]; 25 bool b[maxn]; 26 typedef pair<ll,int> ii; 27 priority_queue<ii,vector<ii>,greater<ii> > q; 28 #define fi first 29 #define se second 30 #define inf 0x7fffffff 31 #define Inf inf*1ll*inf 32 int n; 33 inline void dij(){ 34 for (int i=1;i<=n;i++) dist[i]=Inf; 35 dist[1]=0; 36 q.push(ii(0,1)); 37 while (!q.empty()){ 38 ii u=q.top();q.pop(); 39 if (b[u.se]) continue; 40 b[u.se]=1; 41 for (int i=next[u.se];i;i=edge[i].next) 42 if (dist[u.se]+edge[i].dist<dist[edge[i].to]) { 43 dist[edge[i].to]=dist[u.se]+edge[i].dist; 44 q.push(ii(dist[edge[i].to],edge[i].to)); 45 } 46 } 47 } 48 int p[maxn],gap[maxn],h[maxn],s,t,N; 49 ll sap(int u,ll flow){ 50 if (u==t) return flow; 51 ll cnt=0; 52 for (int i=p[u];i;i=edge[i].next) 53 if (edge[i].cap&&h[edge[i].to]+1==h[u]) { 54 ll cur=sap(edge[i].to,min(edge[i].cap,flow-cnt)); 55 edge[i].cap-=cur;edge[i^1].cap+=cur; 56 p[u]=i; 57 if ((cnt+=cur)==flow) return flow; 58 } 59 if (!(--gap[h[u]])) h[s]=N; 60 gap[++h[u]]++; 61 p[u]=next[u]; 62 return cnt; 63 } 64 inline ll maxflow(){ 65 for (int i=1;i<=N;i++) p[i]=next[i]; 66 ll flow=0; 67 gap[0]=N; 68 while (h[s]<N) flow+=sap(s,Inf); 69 return flow; 70 } 71 int main(){ 72 freopen("network.in","r",stdin); 73 freopen("network.out","w",stdout); 74 int m; 75 scanf("%d%d",&n,&m); 76 N=n*2; 77 for (int i=1;i<=m;i++) { 78 int x,y,z; 79 scanf("%d%d%d",&x,&y,&z); 80 _addedge(x,y,z); 81 } 82 dij(); 83 memset(next,0,sizeof(next)); 84 l=0; 85 for (int i=2;i<=m*2+1;i+=2) { 86 if (dist[edge[i].to]==dist[edge[i^1].to]+edge[i].dist) 87 addedge(n+edge[i^1].to,edge[i].to,Inf); 88 else if (dist[edge[i^1].to]==dist[edge[i].to]+edge[i^1].dist) 89 addedge(n+edge[i].to,edge[i^1].to,Inf); 90 } 91 for (int i=1;i<=n;i++) { 92 int x; 93 scanf("%d",&x); 94 addedge(i,n+i,x); 95 } 96 s=1+n,t=n; 97 printf("%lld ",maxflow()); 98 return 0; 99 }
T3：[CQOI2015]任务查询系统
描述：戳我~~~
这道题首先很明显是道裸的数据结构题啦。首先他要求在线，那么按顺序建个函数式线段树就行啦
自己太弱调了好久= =
CODE：
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 typedef long long ll; 8 #define pb push_back 9 #define maxn 100100 10 struct qnode{ 11 int x,y,z; 12 }q[maxn*2]; 13 int l; 14 inline void add(int x,int y,int z) {q[++l]=(qnode){x,y,z};} 15 bool cmp(qnode x,qnode y) {return x.x<y.x;} 16 struct node{int lc,rc,sum;ll s;}t[maxn*64]; 17 #define mid (l+r>>1) 18 int cnt=0; 19 int ins(int x,int l,int r,int y,int z){ 20 int root=++cnt; 21 t[root]=t[x]; 22 t[root].s+=y*z; 23 t[root].sum+=z; 24 if (l==r) return root; 25 if (y<=mid) t[root].lc=ins(t[x].lc,l,mid,y,z); 26 else t[root].rc=ins(t[x].rc,mid+1,r,y,z); 27 return root; 28 } 29 ll que(int x,int l,int r,int &k){ 30 if (t[x].sum<=k) { 31 k-=t[x].sum;return t[x].s; 32 } 33 if (l==r) {ll ans=l*1ll*k;k=0;return ans;} 34 ll ans=que(t[x].lc,l,mid,k); 35 if (k) ans+=que(t[x].rc,mid+1,r,k); 36 return ans; 37 } 38 vector<int> a; 39 int s[maxn],e[maxn],p[maxn],root[maxn]; 40 int main(){ 41 int n,m; 42 scanf("%d%d",&n,&m); 43 a.pb(0); 44 for (int i=1;i<=n;i++) { 45 scanf("%d%d%d",s+i,e+i,p+i); 46 e[i]++; 47 a.pb(s[i]);a.pb(e[i]); 48 } 49 sort(a.begin(),a.end()); 50 a.resize(unique(a.begin(),a.end())-a.begin()); 51 for (int i=1;i<=n;i++) { 52 add(lower_bound(a.begin(),a.end(),s[i])-a.begin(),p[i],1); 53 add(lower_bound(a.begin(),a.end(),e[i])-a.begin(),p[i],-1); 54 } 55 sort(q+1,q+1+l,cmp); 56 #define inf 10000000 57 for (int i=1;i<=l;i++) root[q[i].x]=ins(root[q[i-1].x],1,inf,q[i].y,q[i].z); 58 ll pre=1; 59 for (int i=1;i<=m;i++) { 60 int x,ai,bi,ci; 61 scanf("%d%d%d%d ",&x,&ai,&bi,&ci); 62 int k=1ll+(ai*1ll*(pre%ci)%ci+bi)%ci; 63 pre=que(root[upper_bound(a.begin(),a.end(),x)-a.begin()-1],1,inf,k); 64 printf("%lld ",pre); 65 } 66 return 0; 67 }
T4：[CQOI2015]多项式
描述：戳我~~~
又是高精度= =
首先我们可以换一下元，吧x-t换成x那就能得到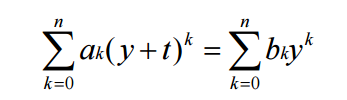
那么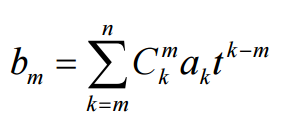
就能算5次即可啦，再考虑怎么快速算组合数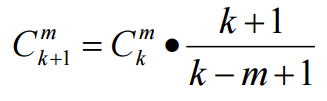
完成啦
CODE：
1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #define maxb 4 6 using namespace std; 7 char s[10010]; 8 int p[9]={1,10,100,1000,10000,100000,1000000,10000000,100000000}; 9 struct bignum{ 10 int a[10010],n,flag; 11 bignum(int x){ 12 n=0;memset(a,0,sizeof(a)); 13 flag=x<0?1:0;x=abs(x); 14 while (x) {a[++n]=x%p[maxb];x/=p[maxb];} 15 if (!n) n=1; 16 } 17 bignum(){n=1;memset(a,0,sizeof(a));flag=0;} 18 int read(){ 19 scanf("%s",s); 20 int len=strlen(s); 21 n=0; 22 if (len==1&&s[0]=='0') {a[n=1]=0;return 0;} 23 for (int i=len;i>=1;i-=maxb) { 24 int t=0; 25 if (i>maxb) for (int j=i-maxb+1;j<=i;j++) t=t*10+s[j-1]-'0'; 26 else for (int j=1;j<=i;j++) t=t*10+s[j-1]-'0'; 27 a[++n]=t; 28 } 29 return 0; 30 } 31 int write(){ 32 if (flag) printf("-"); 33 printf("%d",a[n]); 34 for (int i=n-1;i>=1;i--) { 35 for (int j=1;j<maxb;j++) if (a[i]<p[j]) printf("0"); 36 printf("%d",a[i]); 37 } 38 printf(" "); 39 return 0; 40 } 41 int cmp(bignum x){ 42 if (x.n!=n) return (x.n<n); 43 for (int i=n;i>=1;i--) 44 if (x.a[i]!=a[i]) return (x.a[i]<a[i]); 45 return -1; 46 } 47 int div(int x){ 48 int s=0; 49 for (int i=n;i>=1;i--){ 50 s=a[i]+s*p[maxb]; 51 a[i]=s/x; 52 s%=x; 53 } 54 if (n!=1&&!a[n]) n--; 55 return s; 56 } 57 }a,b; 58 bignum operator + (bignum x,bignum y){ 59 if (x.flag^y.flag && x.cmp(y)==0)swap(x,y); 60 if (x.flag==y.flag) { 61 x.n=max(x.n,y.n); 62 for (int i=1;i<=x.n;i++) { 63 x.a[i]+=y.a[i]; 64 x.a[i+1]+=x.a[i]/p[maxb]; 65 x.a[i]%=p[maxb]; 66 } 67 if (x.a[x.n+1]) x.n++; 68 return x; 69 } 70 for (int i=1;i<=x.n;i++) { 71 x.a[i]-=y.a[i]; 72 if (x.a[i]<0) {x.a[i]+=p[maxb];x.a[i+1]--;} 73 while (!x.a[x.n]&&x.n>1) x.n--; 74 } 75 return x; 76 } 77 bignum operator * (bignum x,bignum y){ 78 bignum ans; 79 if (x.n==1&&x.a[1]==0) return ans; 80 if (y.n==1&&y.a[1]==0) return ans; 81 ans.flag=x.flag^y.flag; 82 for (int i=1;i<=x.n;i++) 83 for (int j=1;j<=y.n;j++) { 84 ans.a[i+j-1]+=x.a[i]*y.a[j]; 85 ans.a[i+j]+=ans.a[i+j-1]/p[maxb]; 86 ans.a[i+j-1]%=p[maxb]; 87 } 88 int n=x.n+y.n-1; 89 while (ans.a[n+1]) { 90 n++;ans.a[n+1]+=ans.a[n]/p[maxb]; 91 ans.a[n]%=p[maxb]; 92 } 93 ans.n=n; 94 return ans; 95 } 96 int sum; 97 int main(){ 98 static bignum n,m; 99 int t; 100 n.read(); 101 scanf("%d",&t); 102 m.read(); 103 static int a[4000]; 104 a[0]=1; 105 for (int i=1;i<=3389;i++) a[i]=(a[i-1]*1234+5678) % 3389; 106 static bignum tmp=m; 107 int l=tmp.div(3388); 108 static bignum ans,c=bignum(1),T=bignum(1); 109 int cnt=0; 110 for (bignum i=m;i.cmp(n)!=1;i=i+bignum(1),cnt++) { 111 ans=ans+c*T*bignum(a[l]); 112 l=(l+1)%3388; 113 c=c*(i+bignum(1)); 114 c.div(cnt+1); 115 T=T*bignum(t); 116 } 117 ans.write(); 118 return 0; 119 }
T5:[CQOI2015]标示设计
描述：戳我~~~
首先我们考虑轮廓线，那么每个L可能有四种状态：已经结束，还未开始，还没拐弯，已经拐弯，那么如果从上到下，从左到右做的话，可以发现最多只有3条横边被标记，那么对每个L我们可以用一维来存这个状态，在加上起始状态还有终止状态就行啦，然后已经拐弯的状态一定是在那条竖边上在讨论下就行啦
由于我是从左到右，从上到下做的，所以每一维就多了1倍的状态，所以在BZ上就光荣的TLE啦，不过在学校的oj上还是能过的。所以代码就不贴啦