零、 Introduction
1.learn over a subset of data
- choose the subset uniformally randomly (均匀随机地选择子集)
- apply some learning algorithm
- 解决第一个问题 :Boosting 算法
- 不再随机选择样本,而是选择the samples we are not good at?
- 寻找算法解决我们当下不知道如何解决的问题——学习的意义
- baic idea behind boosting : focus on the “hardest” examples
2.how do you combine all of those rules of thumbs by saying?
(如何合并凭经验得到的所有规则)
-
weighted Mean
-
Bagging 算法
-
Keyword
- emsembles are good
- bagging is good
- combing simple -> complex
- boosting is really good
- weak learner
- error
一、集成方法(Ensemble Method)
集成方法主要包括Bagging和Boosting两种方法。
- Bagging方法
随机森林算法是基于Bagging思想的机器学习算法,在Bagging方法中,主要通过对训练数据集进行随机采样,以重新组合成不同的数据集,利用弱学习算法对不同的新数据集进行学习,得到一系列的预测结果,对这些预测结果做平均或者投票做出最终的预测。
- AdaBoost算法
AdaBoost算法和GBDT(Gradient Boost Decision Tree,梯度提升决策树)算法是基于Boosting思想的机器学习算法。在Boosting思想中是通过对样本进行不同的赋值,对错误学习的样本的权重设置的较大,这样,在后续的学习中集中处理难学的样本,最终得到一系列的预测结果,每个预测结果有一个权重,较大的权重表示该预测效果较好。
二、AdaBoost算法思想
- “hardest examples”
- “weighted mean ”
AdaBoost算法是基于Boosting思想的机器学习算法,其中AdaBoost是Adaptive Boosting的缩写,AdaBoost是一种迭代型的算法,其核心思想是针对同一个训练集训练不同的学习算法,即弱学习算法,然后将这些弱学习算法集合起来,构造一个更强的最终学习算法。
为了构造出一个强的学习算法,首先需要选定一个弱学习算法,并利用同一个训练集不断训练弱学习算法,以提升弱学习算法的性能。在AdaBoost算法中,有两个权重,第一个数训练集中每个样本有一个权重,称为样本权重,用向量(D)表示;另一个是每一个弱学习算法具有一个权重,用向量(alpha)表示。假设有(N)个样本的训练集
({(X_1,y_1),(X_2,y_2),cdots,(X_n,y_n)} ),初始时,设定每个样本的权重是相等的,即(frac{1}{n}),利用第一个弱学习算法(h_1)对其进行学习,学习完成后进行错误率(varepsilon)的统计:
其中,(error)表示被错误分类的样本数目,(all)表示所有样本的数目。这样便可以利用错误率(varepsilon)计算弱学习算法的权重(alpha _1):
在第一次学习完成后,需要重新调整样本的权重,以使得在第一分类中被错分的样本的权重,使得在接下来的学习中可以重点对其进行学习:
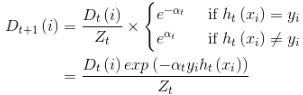
其中,表示(h_t(x_i) = y_i)对第(i)个样本训练正确,(h_t(x_i) eq y_i)表示对第(i)个样本训练错误。是一个(Z_t)归一化因子:(Z_t = sum (D))
这样进行第二次的学习,当学习t轮后,得到了t个弱学习算法({ h_1,cdots,h_t})及其权重({ alpha_1,cdots,alpha_t})。对新的分类数据,分别计算t个弱分类器的输出({ h_1(X),cdots,h_t(X)}),最终的AdaBoost算法的输出结果为:
(H(X) = sign (sum_{i=1}^t alpha_i h_i( X ) ))
其中,是(sign(x))符号函数。具体过程可见下图所示:
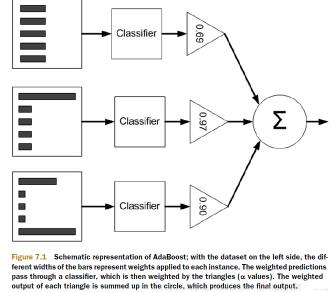
三、AdaBoost算法流程
上述为AdaBoost的基本原理,下面给出AdaBoost算法的流程:

Boost 算法伪代码
-
Given training ({(x_i,y_i)} ) ,(y_i in {-1,+1})
-
For t = 1 to T
- construct distribution (D_t)
- find weak classifier (h_t(x))
with small error
( epsilon_t = P_{D_{scriptsize t}} [h_t(x_i) eq y_i]) -
Output ( H_{final} )
四、Adaboost之python实现
AdaBoost算法是一种具有很高精度的分类器,其实AdaBoost算法提供的是一种框架,在这种框架下,我们可以使用不同的弱分类器,通过AdaBoost框架构建出强分类器。下面我们使用单层决策树构建一个分类器处理如下的分类问题:

决策树算法主要有ID3,C4.5和CART,其中ID3和C4.5主要用于分类,CART可以解决回归问题。
#coding:UTF-8
'''''
Created on 2017年2月22日
@author: P50
'''
from numpy import *
def loadSimpleData():
datMat = mat([[1., 2.1],
[2., 1.1],
[1.3, 1.],
[1., 1.],
[2., 1.]])
classLabels = mat([1.0, 1.0, -1.0, -1.0, 1.0])
return datMat, classLabels
def singleStumpClassipy(dataMat, dim, threshold, thresholdIneq):
classMat = ones((shape(dataMat)[0], 1))
#根据thresholdIneq划分出不同的类,在'-1'和'1'之间切换
if thresholdIneq == 'left':#在threshold左侧的为'-1'
classMat[dataMat[:, dim] <= threshold] = -1.0
else:
classMat[dataMat[:, dim] > threshold] = -1.0
return classMat
def singleStump(dataArr, classLabels, D):
dataMat = mat(dataArr)
labelMat = mat(classLabels).T
m, n = shape(dataMat)
numSteps = 10.0
bestStump = {}
bestClasEst = zeros((m, 1))
minError = inf
for i in xrange(n):#对每一个特征
#取第i列特征的最小值和最大值,以确定步长
rangeMin = dataMat[:, i].min()
rangeMax = dataMat[:, i].max()
stepSize = (rangeMax - rangeMin) / numSteps
for j in xrange(-1, int(numSteps) + 1):
#不确定是哪个属于类'-1',哪个属于类'1',分两种情况
for inequal in ['left', 'right']:
threshold = rangeMin + j * stepSize#得到每个划分的阈值
predictionClass = singleStumpClassipy(dataMat, i, threshold, inequal)
errorMat = ones((m, 1))
errorMat[predictionClass == labelMat] = 0
weightedError = D.T * errorMat#D是每个样本的权重
if weightedError < minError:
minError = weightedError
bestClasEst = predictionClass.copy()
bestStump['dim'] = i
bestStump['threshold'] = threshold
bestStump['inequal'] = inequal
return bestStump, minError, bestClasEst
def adaBoostTrain(dataArr, classLabels, G):
weakClassArr = []
m = shape(dataArr)[0]#样本个数 ,row
### Numpy 之 Shape ###
# 建立一个4×2的矩阵c
# >>> c = array([[1,1],[1,2],[1,3],[1,4]])
# >>> c.shape
# (4, 2)
# >>> c.shape[0]
# 4
# >>> c.shape[1]
# 2
### ###
#初始化D,即每个样本的权重均为1/n
D = mat(ones((n, 1)) / m)
###
# ones(3,3) 可以用来构造(3,3)全一矩阵
aggClasEst = mat(zeros((m, 1)))
for i in xrange(G):#G表示的是迭代次数
bestStump, minError, bestClasEst = singleStump(dataArr, classLabels, D)
print 'D:', D.T
#计算分类器的权重
alpha = float(0.5 * log((1.0 - minError) / max(minError, 1e-16)))
bestStump['alpha'] = alpha
weakClassArr.append(bestStump)
print 'bestClasEst:', bestClasEst.T
#重新计算每个样本的权重D
expon = multiply(-1 * alpha * mat(classLabels).T, bestClasEst)
D = multiply(D, exp(expon))
D = D / D.sum()
aggClasEst += alpha * bestClasEst
print 'aggClasEst:', aggClasEst
aggErrors = multiply(sign(aggClasEst) != mat(classLabels).T, ones((m, 1)))
errorRate = aggErrors.sum() / m
print 'total error:', errorRate
if errorRate == 0.0:
break
return weakClassArr
def adaBoostClassify(testData, weakClassify):
dataMat = mat(testData)
m = shape(dataMat)[0]
aggClassEst = mat(zeros((m, 1)))
for i in xrange(len(weakClassify)):#weakClassify是一个列表
classEst = singleStumpClassipy(dataMat, weakClassify[i]['dim'], weakClassify[i]['threshold'], weakClassify[i]['inequal'])
aggClassEst += weakClassify[i]['alpha'] * classEst
print aggClassEst
return sign(aggClassEst)
if __name__ == '__main__':
datMat, classLabels = loadSimpleData()
weakClassArr = adaBoostTrain(datMat, classLabels, 30)
print "weakClassArr:", weakClassArr
#test
result = adaBoostClassify([1, 1], weakClassArr)
print result
OUTPUT:
weakClassArr: [{'threshold': 1.3, 'dim': 0, 'inequal': 'left', 'alpha': 0.6931471805599453},
{'threshold': 1.0, 'dim': 1, 'inequal': 'left', 'alpha': 0.9729550745276565}, {'threshold':
0.90000000000000002, 'dim': 0, 'inequal': 'left', 'alpha': 0.8958797346140273}]
[[-0.69314718]]
[[-1.66610226]]
[[-0.77022252]]
[[-1.]]
五、思考
5.1 回答Introduction中的问题
(i)每一次训练如何选择不同分布?
答:给先前学习规则分类错误的样本更高的权重,正确分类样本权重降低,
使弱学习器能够更集中解决这些“困难”的样本。
简单的来说,分类正确的样本我们可以不用再分了,错误分类的才是主要敌人。
(ii)如何将产生的众多弱规则整合成一个规则?
答:按照它们的预测结果通过‘投票法’产生,少数服从多数。
5.2 为什么 Boosting 算法 的效果 这么好?
分布:让上一次被错误分类的样本 越来越重要 (增加权重)
误差不会上升——每次迭代必定比随机猜测更好(即每次错误率必小于随机概率0.5)
逆向推理:什么情况下效果不好
还有大量样本分类错误
5.3 Boosting & 过拟合
boosting 往往不会过拟合,但这种情况仍然有可能会发生
回顾 SVM
solution : try to focus on maximum margin classfiers
(集中在最大边缘分类器上)
large margins tend to minimize over fitting
Boosting
+error
+confidence (置信度):
general definition:how strongly you believe in a particular answer that you given.
in the boosting case: h_final
boosting 往往不会过拟合,但这种情况仍然有可能会发生
- possible overfitting case:
1.□ 进行 Boosting 的弱学习方法是含有多次网络和多个节点的神经网络
若boosting调用 ANN算法时发生过拟合 且返回值没有误差,all the examples will have equal weight.
when you go through the loop again,you will just call the same learner,which will use the same neural network,and will return the same neural network.
每次调用学习器时,你都会得到零训练误差。但所得的神经网络也是相同的。就此陷入恶性循环。
小结:如果你的基础学习器本身产生了过拟合,那么Boosting很难克服这一点。
- the case of pink noise
pink noise just means uniform noise.
P.S. white noise is Gaussian noise
pink noise is uniform noise.
*不是过拟合的原因:
□ Boosting 训练的时间过长(极限思想,趋向于分离样本)
5.4 加权组合 回到最初的起点
通过简单组合 获得更复杂事物
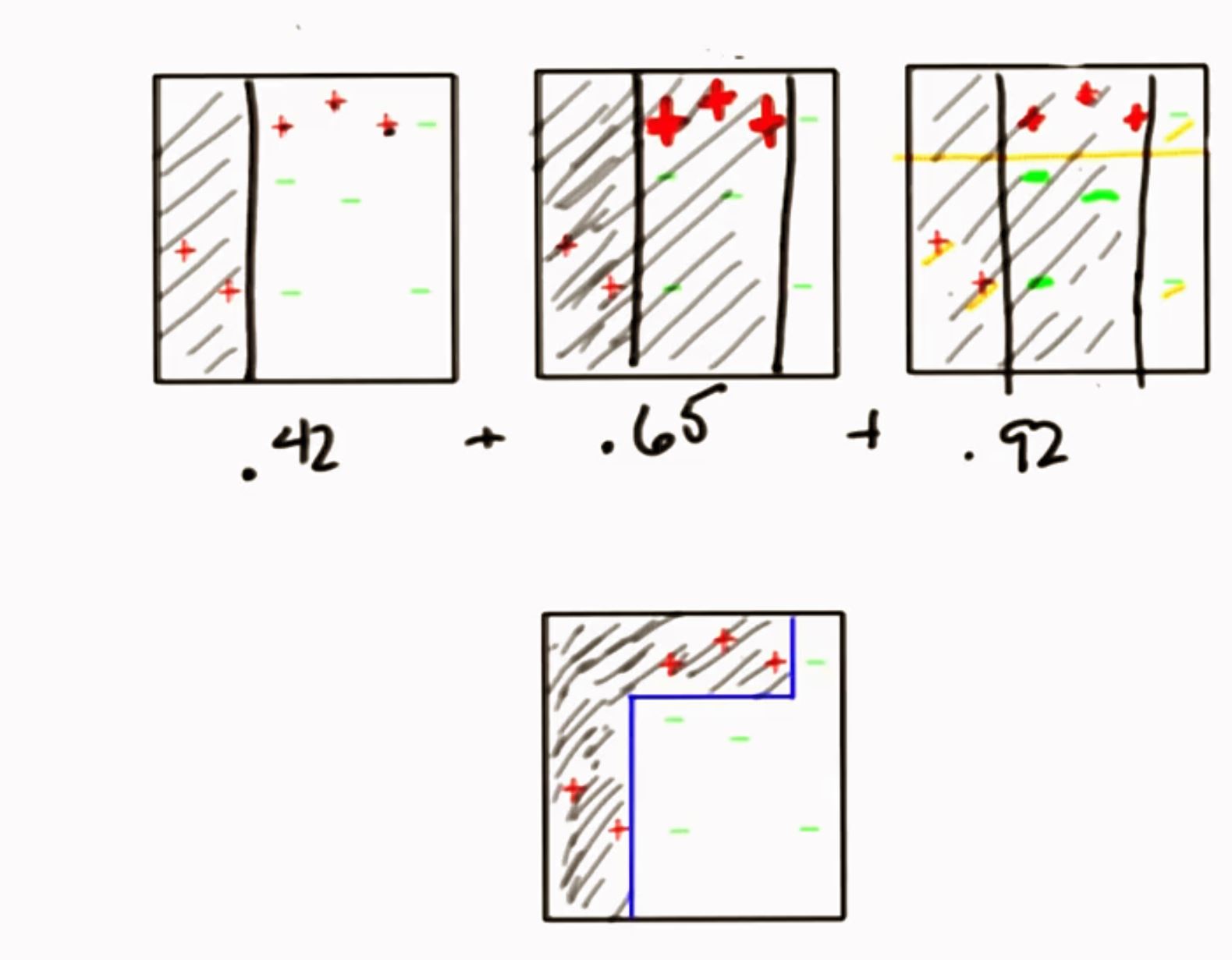
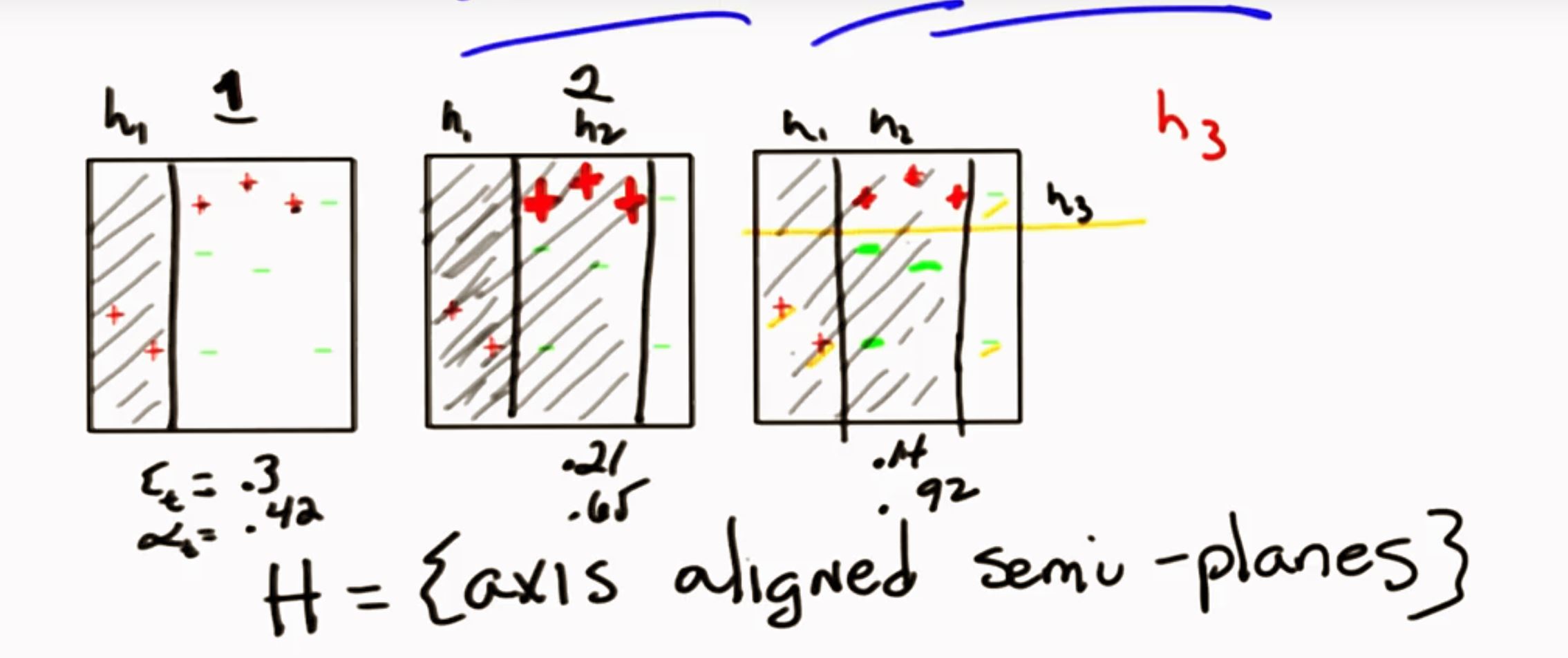
参考链接:
http://blog.csdn.net/gamer_gyt/article/details/51372309
http://discussions.youdaxue.com/t/boosting/45579
http://blog.csdn.net/google19890102/article/details/46507387
https://www.cnblogs.com/csyuan/p/6537255.html
http://blog.sina.com.cn/s/blog_13ec1876a0102xboj.html
http://blog.csdn.net/google19890102/article/details/46376603
参考论文
1.Introduction to Boosting By Udacity
2.The Boosting Approach to Machine Learning By AT&T Labs Research Shannon Laborator