ANN神经网络——Sigmoid 激活函数编程练习 (Python实现)

# ----------
# 
# There are two functions  to finish:
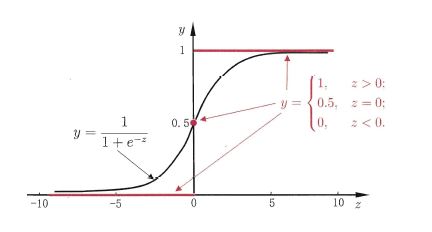
# First, in activate(), write the sigmoid activation function.
# Second, in update(), write the gradient descent update rule. Updates should be
#   performed online, revising the weights after each data point.
# 
# ----------

import numpy as np


class Sigmoid:
    """
    This class models an artificial neuron with sigmoid activation function.
    """

    def __init__(self, weights = np.array([1])):
        """
        Initialize weights based on input arguments. Note that no type-checking
        is being performed here for simplicity of code.
        """
        self.weights = weights

        # NOTE: You do not need to worry about these two attribues for this
        # programming quiz, but these will be useful for if you want to create
        # a network out of these sigmoid units!
        self.last_input = 0 # strength of last input
        self.delta      = 0 # error signal

    def activate(self, values):
        """
        Takes in @param values, a list of numbers equal to length of weights.
        @return the output of a sigmoid unit with given inputs based on unit
        weights.
        """
        
        # YOUR CODE HERE
        
        
        # First calculate the strength of the input signal.
        strength = np.dot(values, self.weights)
        self.last_input = strength
        
        # TODO: Modify strength using the sigmoid activation function and
        # return as output signal.
        # HINT: You may want to create a helper function to compute the
        #   logistic function since you will need it for the update function.
        
        
        result = self.logistic(strength)
        return result
    
    
    def logistic(self,strength):        
        return 1/(1+np.exp(-strength))
        
        
    def update(self, values, train, eta=.1):
        """
        Takes in a 2D array @param values consisting of a LIST of inputs and a
        1D array @param train, consisting of a corresponding list of expected
        outputs. Updates internal weights according to gradient descent using
        these values and an optional learning rate, @param eta.
        """

        # TODO: for each data point...
        for X, y_true in zip(values, train):
            # obtain the output signal for that point
            y_pred = self.activate(X)

            # YOUR CODE HERE

            # TODO: compute derivative of logistic function at input strength
            # Recall: d/dx logistic(x) = logistic(x)*(1-logistic(x))
            dx = self.logistic(self.last_input)*(1 - self.logistic(self.last_input) )
            print ("dx{}:".format(dx))
            print ('
')
            # TODO: update self.weights based on learning rate, signal accuracy,
            # function slope (derivative) and input value
            delta_w = eta * (y_true - y_pred) * dx * X
            print ("delta_w:{} weight before {}".format(delta_w, self.weights))
           
            self.weights += delta_w
            print ("delta_w:{} weight after {}".format(delta_w, self.weights))
            print ('
')

def test():
    """
    A few tests to make sure that the perceptron class performs as expected.
    Nothing should show up in the output if all the assertions pass.
    """
    def sum_almost_equal(array1, array2, tol = 1e-5):
        return sum(abs(array1 - array2)) < tol

    u1 = Sigmoid(weights=[3,-2,1])
    assert abs(u1.activate(np.array([1,2,3])) - 0.880797) < 1e-5
    
    u1.update(np.array([[1,2,3]]),np.array([0]))
    assert sum_almost_equal(u1.weights, np.array([2.990752, -2.018496, 0.972257]))

    u2 = Sigmoid(weights=[0,3,-1])
    u2.update(np.array([[-3,-1,2],[2,1,2]]),np.array([1,0]))
    assert sum_almost_equal(u2.weights, np.array([-0.030739, 2.984961, -1.027437]))

if __name__ == "__main__":
    test()

OUTPUT

Running test()...
dx0.104993585404:


delta_w:[-0.0092478  -0.01849561 -0.02774341] weight before [3, -2, 1]
delta_w:[-0.0092478  -0.01849561 -0.02774341] weight after [ 2.9907522  -2.01849561  0.97225659]


dx0.00664805667079:


delta_w:[-0.00198107 -0.00066036  0.00132071] weight before [0, 3, -1]
delta_w:[-0.00198107 -0.00066036  0.00132071] weight after [ -1.98106867e-03   2.99933964e+00  -9.98679288e-01]


dx0.196791859198:


delta_w:[-0.02875794 -0.01437897 -0.02875794] weight before [ -1.98106867e-03   2.99933964e+00  -9.98679288e-01]
delta_w:[-0.02875794 -0.01437897 -0.02875794] weight after [-0.03073901  2.98496067 -1.02743723]


All done!