• 【纪中受难记】——C3D8：Ctrl+C/V滥用的后果

    考完发现写了两个文件输入。

    爆零了。

    Description

    　　农民John的某 N 头奶牛 (1 <= N <= 80,000) 正在过乱头发节！由于每头牛都意识到自己凌乱不堪的发型，FJ 希望统计出能够看到其他牛的头发的牛的数量。 　　每一头牛 i有一个高度 h[i] (1 <= h[i] <= 1,000,000,000)而且面向东方排成一排(在我们的图中是向右)。因此，第i头牛可以看到她前面的那些牛的头，（即i+1, i+2,等等），只要那些牛的高度严格小于她的高度。
           每一头牛 i有一个高度 h[i] (1 <= h[i] <= 1,000,000,000)而且面向东方排成一排(在我们的图中是向右)。因此，第i头牛可以看到她前面的那些牛的头，（即i+1, i+2,等等），只要那些牛的高度严格小于她的高度。
    例如这个例子:
            =
    =       =
    =       =
    =   -   =           牛面向右侧 -->
    =   =   =
    = - = = =
    = = = = = =
    1 2 3 4 5 6


    牛#1 可以看到她们的发型 #2, 3, 4
    牛#2 不能看到任何牛的发型
    牛#3 可以看到她的发型 #4
    牛#4 不能看到任何牛的发型
    牛#5 可以看到她的发型 6
    牛#6 不能看到任何牛的发型!
    让 c[i] 表示第i头牛可以看到发型的牛的数量；请输出 c[1] 至 c[N]的和。如上面的这个例子，正确解是3 + 0 + 1 + 0 + 1 + 0 = 5。

     

    Input

    Line 1: 牛的数量 N。
    Lines 2..N+1: 第 i+1 是一个整数，表示第i头牛的高度。

    Output

    　　Line 1: 一个整数表示c[1] 至 c[N]的和。
     

    Sample Input

    6
    10
    3
    7
    4
    12
    2

    Sample Output

    5

    用了双向链表（初赛整蒙的玩意）。

    求出右边第一个比它大的值，再拿相对位置处理一下即可。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 ll read(){
 5     ll x=0,f=1;
 6     char c=getchar();
 7     while(!isdigit(c)){
 8         if(c=='-') f=-1;
 9         c=getchar();
10     }
11     while(isdigit(c)){
12         x=(x<<1)+(x<<3)+(c^48);
13         c=getchar();
14     }
15     return x*f;
16 }
17 const int N=80010;
18 struct node{
19     ll pos,h;
20     bool operator < (const node &x)const{
21         if(h==x.h)return pos<x.pos;
22         return h<x.h;
23     }
24 }cow[N];
25 ll pre[N],nxt[N];
26 ll high[N];
27 ll cnt,n;
28 ll ans;
29 int main(){
30 //    freopen("badhair.in","r",stdin);
31 //    freopen("badhair.out","w",stdout);
32     n=read();
33     for(int i=1;i<=n;i++){
34         cow[i].h=read();
35         cow[i].pos=i;
36     }
37     for(int i=1;i<=n;i++){
38         pre[i]=i-1;
39         nxt[i]=i+1;
40     }
41     sort(cow+1,cow+n+1);
42     for(int i=1;i<=n;i++){
43         nxt[pre[cow[i].pos]]=nxt[cow[i].pos];
44         pre[nxt[cow[i].pos]]=pre[cow[i].pos];
45     }
46     ll ans=0;
47     for(int i=1;i<=n;i++)
48         ans+=nxt[i]-i-1;
49         printf("%lld",ans);
50     return 0;
51 }

    Description

           正如你所知，奶牛们没有手指以至于不能玩“石头剪刀布”来任意地决定例如谁先挤奶的顺序。她们甚至也不能通过仍硬币的方式。
           所以她们通过"round number"竞赛的方式。第一头牛选取一个整数，小于20亿。第二头牛也这样选取一个整数。如果这两个数都是 "round numbers"，那么第一头牛获胜，否则第二头牛获胜。
           如果一个正整数N的二进制表示中，0的个数大于或等于1的个数，那么N就被称为"round number" 。例如，整数9，二进制表示是1001，1001 有两个'0'和两个'1'; 因此，9是一个round number。26 的二进制表示是 11010 ; 由于它有2个'0'和3个'1'，所以它不是round number。
           很明显，奶牛们会花费很大精力去转换进制，从而确定谁是胜者。 Bessie 想要作弊，而且认为只要她能够知道在一个指定区间范围内的"round numbers"个数。
           帮助她写一个程序，能够告诉她在一个闭区间中有多少Hround numbers。区间是[start, finish]，包含这两个数。 (1 <= Start < Finish <= 2,000,000,000)

     

    Input

    　　Line 1: 两个用空格分开的整数，分别表示Start 和 Finish。

    Output

    　　Line 1: Start..Finish范围内round numbers的个数
     

    Sample Input

    2 12

    Sample Output

    6
     

    Data Constraint

     
     

    Hint

    【样例说明】
     2    10  1x0 + 1x1  ROUND
     3    11  0x0 + 2x1  NOT round
     4   100  2x0 + 1x1  ROUND
     5   101  1x0 + 2x1  NOT round
     6   110  1x0 + 2x1  NOT round
     7   111  0x0 + 3x1  NOT round
     8  1000  3x0 + 1x1  ROUND
     9  1001  2x0 + 2x1  ROUND
    10  1010  2x0 + 2x1  ROUND
    11  1011  1x0 + 3x1  NOT round
    12  1100  2x0 + 2x1  ROUND

    这题是数位dp，思路慢慢讲。

    考虑一个数100100：

    我们知道100000~1是很好求得答案的：

    1.考虑第2位放1，那么3~6位可以随便放，即1？？？？

    注意到0的数量大于等于1的数量，因此，这部分答案就是：

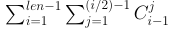
    len为数字二进制位数。

    1     for(int i=len-1;i>=1;i--){
2         for(int j=i/2-1;j>=1;j--){
3             ans+=f[i-1][j];
4         }
5     }

    2.加上形如1000……的答案，结果加上len-1；

    3.对于100100~100000的答案，我们从后往前考虑：

    对于第一个遇到的1（第4位），我们看100100能不能计入答案，如果能就计入，否则无论怎么缩小都是没有意义的，可以直接往前面的1看去。

    这里可以，因此我们计入一个100100，再删去这个位置上的1，考虑后面两位可以怎么放。

    显然，能放的1的个数可以计算得出（可以维护一个前缀和），再套用组合数即可。

    处理完这个就可以往前走了。（建议手推）

     1 for(int i=1;i<=len;i++){
 2         if(s[i]==0) continue;
 3         if(i==len) break;
 4         if(len-sum[i]>=sum[i]) ans++;
 5         else continue;
 6         sum[i]--;
 7         int mon=i-1;
 8         int son=min(mon,len/2-sum[i]);
 9         for(int j=son;j>=1;j--){
10             ans+=f[mon][j];
11         }
12     }

    最后给出全部代码：

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int read(){
 4     int x=0,f=1;
 5     char c=getchar();
 6     while(!isdigit(c)){
 7         if(c=='-') f=-1;
 8         c=getchar();
 9     }
10     while(isdigit(c)){
11         x=(x<<1)+(x<<3)+(c^48);
12         c=getchar();
13     }
14     return x*f;
15 }
16 int st,nd;
17 int f[100][100];
18 int solve(int num){
19     if(!num) return 0;
20     int ans=0;
21     int s[200],sum[200];
22     memset(s,0,sizeof(s));
23     memset(sum,0,sizeof(sum));
24     int len=0;
25     while(num){
26         len++;
27         if(num&1) s[len]=1;
28         num>>=1;
29     }
30     for(int i=len;i>=1;i--){
31         sum[i]=sum[i+1]+s[i];
32     }
33     for(int i=1;i<=len;i++){
34         if(s[i]==0) continue;
35         if(i==len) break;
36         if(len-sum[i]>=sum[i]) ans++;
37         else continue;
38         sum[i]--;
39         int mon=i-1;
40         int son=min(mon,len/2-sum[i]);
41         for(int j=son;j>=1;j--){
42             ans+=f[mon][j];
43         }
44     }
45     for(int i=len-1;i>=1;i--){
46         for(int j=i/2-1;j>=1;j--){
47             ans+=f[i-1][j];
48         }
49     }
50     return ans+len-1;
51 }
52 int main(){
53 //    freopen("rndnum.in","r",stdin);
54 //    freopen("rndnum.out","w",stdout);
55     st=read();nd=read();
56     for(int i=0;i<=33;i++){
57         f[i][0]=1;
58     }
59     for(int i=1;i<=33;i++){
60         for(int j=1;j<=i;j++){
61             f[i][j]=f[i-1][j-1]+f[i-1][j];
62         }
63     }
64     printf("%d",solve(nd)-solve(st-1));
65     return 0;
66 }

    Description

    　　农民 John 购买了一处肥沃的矩形牧场，分成M*N(1 <= M <= 12; 1 <= N <= 12)个格子。他想在那里的一些格子中种植美味的玉米。遗憾的是，有些格子区域的土地是贫瘠的，不能耕种。精明的 FJ 知道奶牛们进食时不喜欢和别的牛相邻，所以一旦在一个格子中种植玉米，那么他就不会在相邻的格子中种植，即没有两个被选中的格子拥有公共边。他还没有最终确定哪些格子要选择种植玉米。 　　        作为一个思想开明的人，农民 John 希望考虑所有可行的选择格子种植方案。由于太开明，他还考虑一个格子都不选择的种植方案！请帮助农民 John 确定种植方案总数。
     

    Input

    　　Line 1: 两个用空格分隔的整数 M 和 N
    　　Lines 2..M+1: 第 i+1 行描述牧场第i行每个格子的情况， N 个用空格分隔的整数，表示 这个格子是否可以种植(1 表示肥沃的、适合种植，0 表示贫瘠的、不可种植)

    Output

    　　Line 1: 一个整数: FJ 可选择的方案总数 除以 100,000,000 的余数。
     

    Sample Input

    2 3
    1 1 1
    0 1 0

    Sample Output

    9
     

    Data Constraint

     
     

    Hint

    【样例说明】
    给可以种植玉米的格子编号:
    1 2 3
      4
    只种一个格子的方案有四种 (1, 2, 3, 或 4)，种植两个格子的方案有三种 (13, 14, 或 34)，种植三个格子的方案有一种 (134)，还有一种什么格子都不种。 4+3+1+1=9。

    状压板子，我起了，一枪秒了，没什么好说的。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 int read(){
 5     int x=0,ff=1;
 6     char c=getchar();
 7     while(!isdigit(c)){
 8         if(c=='-') ff=-1;
 9         c=getchar();
10     }
11     while(isdigit(c)){
12         x=(x<<1)+(x<<3)+(c^48);
13         c=getchar();
14     }
15     return x*ff;
16 }
17 const int N=15;
18 const int mod=1e8;
19 int m,n;
20 ll fix[N];
21 ll f[N][1<<N];
22 int main(){
23 //    freopen("cowfood.in","r",stdin);
24 //    freopen("cowfood.out","w",stdout);
25     m=read();n=read();
26     memset(f,0,sizeof(f));
27     for(int i=1,num;i<=m;i++){
28         for(int j=1;j<=n;j++){
29             num=read();
30             fix[i]=(fix[i]<<1)+num^1;
31         }
32     }
33     for(int i=0;i<(1<<n);i++){
34         if((i&fix[1])||(i&(i<<1))||(i&(i>>1))) continue;
35         f[1][i]=1;
36     }
37     for(int i=2;i<=m;i++){
38         for(int j=0;j<(1<<n);j++){
39             if((j&(j<<1))||(j&(j>>1))||(j&fix[i-1])) continue;
40             for(int k=0;k<(1<<n);k++){
41                 if((j&k)||(k&fix[i])||(k&(k<<1))||(k&(k>>1))) continue;
42                 f[i][k]=(f[i][k]+f[i-1][j])%mod;
43             }
44         }    
45     }
46     ll ans=0;
47     for(int i=0;i<(1<<n);i++) ans=(ans+f[m][i])%mod;
48     printf("%lld",ans);
49     return 0;
50 }

    Description

    　　Bessie 来到一个小农场，有时她想回老家看看她的一位好友。她不想太早地回到老家，因为她喜欢途中的美丽风景。她决定选择次短路径，而不是最短路径。
    　　农村有 R (1 <= R <= 100,000) 条双向的路，每条路连接 N (1 <= N <= 5000) 个结点中的两个。结点的编号是 1..N。Bessie 从结点 1出发，她的朋友（目的地）在结点 N。
    　　次短路径可以使用最短路径上的路，而且允许退回，即到达一个结点超过一次。次短路径是一种长度大于最短路径的路径(如果存在两条或多条最短路径存在，次短路径就是比它们长，且不比其他任何的路径长的路径）。
     

    Input

    　　Line 1: 两个用空格分隔的整数 N 和 R
    　　Lines 2..R+1: 每行包含三个用空格分隔的整数： A, B, 和 D表示有一条路连接结点A和B，长度为D (1 <= D <= 5000)。

    Output

    　　Line 1: 结点 1 到结点 N的次短路径长度。
     

    Sample Input

    4 4
    1 2 100
    2 4 200
    2 3 250
    3 4 100

    Sample Output

    450
     

    Data Constraint

     
     

    Hint

    【样例说明】
    两条路径： 1 -> 2 -> 4 (长度 100+200=300) 以及 1 -> 2 -> 3 -> 4(长度 100+250+100=450)

    求次短路径。

    拿另外一个dis2来保存次短的，考虑两种情况：

    1.找到一条路径，发现可以更新最短路：

    　　把这条路径给最短路，最短路的那条给次短路即可。

    2.找到一条路径比最短路长但比次短路短：

    　　给次短路即可。

    注意次序。

     1 #include<bits/stdc++.h>
 2 #include<queue>
 3 using namespace std;
 4 int read(){
 5     int x=0,f=1;
 6     char c=getchar();
 7     while(!isdigit(c)){
 8         if(c=='-') f=-1;
 9         c=getchar();
10     }
11     while(isdigit(c)){
12         x=(x<<1)+(x<<3)+(c^48);
13         c=getchar();
14     }
15     return x*f;
16 }
17 const int N=1e5+10;
18 int n,m;
19 struct edge{
20     int to,next,w;
21 }e[N<<1];
22 int head[N<<1],cnt;
23 void addedge(int from,int to,int w){
24     e[++cnt]=(edge){to,head[from],w};
25     head[from]=cnt;
26 }
27 int dis[N],dis2[N];
28 struct node{
29     int pos,dis;
30     bool operator < (const node&x)const{
31         return dis>x.dis;
32     }
33 };
34 priority_queue<node> q;
35 void dij(){
36     memset(dis,0x3f,sizeof(dis));
37     memset(dis2,0x3f,sizeof(dis2));
38     dis[1]=0;
39     q.push((node){1,0});
40     while(!q.empty()){
41         node tmp=q.top();
42         q.pop();
43         int u=tmp.pos,w1=tmp.dis;
44         if(dis2[u]<tmp.dis) continue;
45         for(int i=head[u];i;i=e[i].next){
46             int v=e[i].to,w=e[i].w+w1;
47             if(w<dis[v]){
48                 swap(dis[v],w);
49                 q.push((node){v,dis[v]});
50             }
51             if(dis[v]<w&&w<dis2[v]){
52                 dis2[v]=w;
53                 q.push((node){v,dis2[v]});
54             }
55         }
56     }
57 }
58 int main(){
59 //    freopen("block.in","r",stdin);
60 //    freopen("block.out","w",stdout);
61     n=read();m=read();
62     for(int i=1,x,y,z;i<=m;i++){
63         x=read();y=read();z=read();
64         addedge(x,y,z);
65         addedge(y,x,z);
66     }
67     dij();
68     printf("%d",dis2[n]);
69     return 0;
70 }
    ——抓住了时间，却不会利用的人，终究也逃不过失败的命运。
  • 相关阅读:
    scan chain的原理和实现——3.Tester Timing
    pattern——serial/paralel
    Scan and ATPG (Tessent)----1.基础概念
    ipdb介绍及Tensor
    pytorch简介
    Python 之map、filter、reduce
    分类器、logistic回归
    机器学习方法、距离度量、K_Means
    动态规划、图
    T分布
  • 原文地址：https://www.cnblogs.com/Nelson992770019/p/11843029.html
Copyright © 2020-2023  润新知