• 【纪中受难记】——C3D4：万里无云

    万里无云，又是平静的一天。

    Description

    给定一个由小写字母组成的字符串，寻找包含“agnus”（羔羊）的子串的个数。注意：当且仅当两个子串的起始位置和终点不同时，这两个子串属于不同的子串。
     

    Input

    只有一个字符串，表示题中所述的字符串。

    Output

    仅一个数字，表示满足题意的子串个数。
     

    Sample Input

    agnusbgnus

    Sample Output

    6
    【样例解释】
        6个子串分别是：agnus、agnusb、agnusbg、agnusbgn、agnusbgnu、agnusbgnus。
     

    Data Constraint

    对于 40%的数据，字符串长度<=1000
    对于 100%的数据，字符串长度<=30000

    On遍历串，找到s就判一下是否形成agnus，如果形成就统计（乘法原理）。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 char c[30010];
 4 bool isagnus(int i){
 5     return (c[i-4]=='a'&&c[i-3]=='g'&&c[i-2]=='n'&&c[i-1]=='u');
 6 }
 7 int nxt;
 8 long long ans;
 9 int main(){
10     cin>>c;
11     nxt=-1;
12     int len=strlen(c);
13     for(int i=0;i<len;i++){
14         if(c[i]=='s'){
15             if(isagnus(i)){
16                 ans+=(i-4-nxt)*(len-i);
17                 nxt=i-4;
18             }
19         }
20     }
21     printf("%d",ans);
22     return 0;
23 }

    Description

    SJY有一天被LLT紧急召去计算一些可能的损失。LLT元首管理的SHB国的交通形成了一棵树，现在将会出现一颗陨石砸在SHB国中，并且陨石砸毁的必定是SHB国构成的交通树上的一条路径。SHB国的损失可表示为被砸毁的路径上的所有城市价值之积。现在还暂时无法确定陨石的掉落路线，所以LLT元首希望SJY能够告诉他SHB国在受到每一种砸毁方式后会受到的损失之和模10086之后的值。注意：单独一个节点也被认为是合法的路径。
     

    Input

    第1行一个数n，表示城市数。
    第2行n个数，第i个数表示第i个城市的价值。
    第3到n+1行，每行两个数u,v，表示城市u,v之间有一条道路。

    Output

    包含一个数，表示SHB国将受到的损失之和。
     

    Sample Input

    5
    7 6 6 1 1 
    1 2
    2 3
    2 4
    1 5

    Sample Output

    778
     

    Data Constraint

    对于20%的数据，n<=100;
    对于50%的数据，n<=3000;
    对于100%的数据，n<=100000。

    考虑dp，用f[i][0/1]分别表示从以i为根节点的子树中，经过点i而是否上去的路径答案。

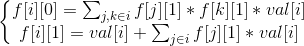
    发现处理f[i][0]时复杂度似乎太高，考虑优化：

    用v表示f[v][1]：

     这样就能在线维护了。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int read(){
 4     int x=0,f=1;
 5     char c=getchar();
 6     while(!isdigit(c)){
 7         if(c=='-') f=-1;
 8         c=getchar();
 9     }
10     while(isdigit(c)){
11         x=(x<<1)+(x<<3)+(c^48);
12         c=getchar();
13     }
14     return x*f;
15 }
16 typedef long long ll;
17 const int N=1e5+10;
18 const int p=10086;
19 ll val[N];
20 ll f[N][2];
21 int n;
22 struct edge{ int to,nxt; }e[N<<1];
23 int head[N<<1],cnt;
24 void addedge(int from,int to){e[++cnt]=(edge){to,head[from]};head[from]=cnt;}
25 void dfs(int u,int fa){
26     f[u][1]=(val[u])%p;
27     ll tot=0,sum=0;
28     for(int i=head[u];i;i=e[i].nxt){
29         int v=e[i].to;
30         if(v==fa) continue;
31         dfs(v,u);
32         tot=f[v][1];
33         f[u][0]=(f[u][0]+tot*sum*val[u])%p;
34         sum=(sum+tot)%p;
35         f[u][1]=(f[u][1]+f[v][1]*val[u])%p;
36     }
37 }
38 int main(){
39     n=read();
40     for(int i=1;i<=n;i++) val[i]=read();
41     for(int i=1,x,y;i<n;i++){
42         x=read(),y=read();
43         addedge(x,y);
44         addedge(y,x);
45     }
46     dfs(1,0);
47     ll ans=0;
48     for(int i=1;i<=n;i++){
49         ans=(ans+f[i][0]+f[i][1])%p;
50     }
51     printf("%lld",ans);
52     return 0;
53 }

    Description

    dzy 手上有一张n 个点m 条边的联通无向图，仙人掌是一张每条边最多在一个简单环内的联通无向图。他想求这个无向图的生成仙人掌中最多有多少条边。
    但是dzy 觉得这个问题太简单了，于是他定义了“美丽的生成仙人掌”，即在一个生成仙人掌中如果满足对于任意编号为i，j(i < j) 的两点，存在一条它们之间的简单路径上面有j-i+1 个点，则这个仙人掌是美丽的。
    他现在想要知道这张图的美丽的生成仙人掌中最多有多少条边，你能帮帮他吗？
     

    Input

    第一行两个整数n，m。接下来m 行每行两个整数ui,vi，表示这两个点之间有一条无向边。保证图中没有自环。

    Output

    仅一行一个整数表示答案。
     

    Sample Input

    2 1
    1 2

    Sample Output

    1
     

    Data Constraint

    对于10% 的数据，n <=10。
    对于30% 的数据，n <=10^3。
    对于100% 的数据，n <=10^5,m <= 2n。

    分析题。

    发现如果存在一个图满足条件，那么它一定是一条编号连续的链，用一些边将其中的点连接。

    又发现这道题不用图论，直接dp即可（找的就是不相交线段条数）。

     1 #include<bits/stdc++.h>
 2 #pragma GCC optimize(3)
 3 using namespace std;
 4 int read(){
 5     int x=0,f=1;
 6     char c=getchar();
 7     while(!isdigit(c)){
 8         if(c=='-') f=-1;
 9         c=getchar();
10     }
11     while(isdigit(c)){
12         x=(x<<1)+(x<<3)+(c^48);
13         c=getchar();
14     }
15     return x*f;
16 }
17 const int N=2e5+10;
18 int n,m;
19 int f[N];
20 int l[N];
21 int main(){
22     n=read();m=read();
23     for(register int i=1;i<=m;i++){
24         int ll=read(),rr=read();
25         if(ll>rr) swap(ll,rr);
26         if(ll<rr-1){
27             l[rr]=max(l[rr],ll);
28         }
29     }
30     for(register int i=1;i<=n;i++){
31         if(l[i]) f[i]=max(f[i-1],f[l[i]]+1);
32         else f[i]=f[i-1];
33     }
34     printf("%d",f[n]+n-1);
35     return 0;
36 }
    ——抓住了时间，却不会利用的人，终究也逃不过失败的命运。
  • 相关阅读:
    【转】jmeter学习笔记——如何使用镜像服务器
    【转】jmeter学习笔记——分布式测试
    【转】jmeter学习笔记——一种简单的数据库性能测试方法
    【转】jmeter学习笔记——JDBC测试计划－连接Mysql
    【转】jmeter学习笔记——集合点
    【转】jmeter学习笔记——检查点
    【转】jmeter学习笔记——参数化
    【转】jmeter学习笔记——关联
    python笔记-字符串连接
    python3笔记-读取ini配置文件
  • 原文地址：https://www.cnblogs.com/Nelson992770019/p/11805330.html
Copyright © 2020-2023  润新知