• 【纪中受难记】——C2Day2：dp不能

    败在了dp上。

    100/0/100/0

    Description

    【问题背景】
    　　LHX教主最近总困扰于前来膜拜他的人太多了，所以他给他的花园加上了一道屏障。 

    【问题描述】
    　　可以把教主的花园附近区域抽像成一个正方形网格组成的网络，每个网格都对应了一个坐标（均为整数，有可能为负），若两个网格(x1, y1)，(x2, y2)有|x1 – x2| + |y1 – y2| = 1，则说这两个网格是相邻的，否则不是相邻的。
    　　教主在y = 0处整条直线上的网格设置了一道屏障，即所有坐标为(x, 0)的网格。当然，他还要解决他自己与内部人员的进出问题，这样教主设置了N个入口a1, a2, …, aN可供进出，即对于y = 0上的所有网格，只有 (a1, 0)，(a2, 0)， ……， (aN, 0) 可以通过，之外的所有纵坐标为0的网格均不能通过，而对于(x, y)有y不为0的网格可以认为是随意通过的。
    　　现在教主想知道，给定M个点对(x1, y1)，(x2, y2)，并且这些点均不在屏障上，询问从一个点走到另一个点最短距离是多少，每次只能从一个格子走到相邻的格子。
     

    Input

    　　输入的第1行为一个正整数N，为屏障上入口的个数。
    　　第2行有N个整数，a1, a2, …, aN，之间用空格隔开，为这N个入口的横坐标。
    　　第3行为一个正整数M，表示了M个询问。
    　　接下来M行，每行4个整数x1, y1, x2, y2，有y1与y2均不等于0，表示了一个询问从(x1, y1)到(x2, y2)的最短路。

    Output

    　　输出共包含m行，第i行对于第i个询问输出从(x1, y1)到(x2, y2)的最短路距离是多少。
     

    Sample Input

    2
2 -1
2
0 1 0 -1
1 1 2 2

    Sample Output

    4
2
     

    Data Constraint

     
     

    Hint

    【数据规模】
    　　对于20%的数据，有n，m≤10，ai，xi，yi绝对值不超过100；
    　　对于40%的数据，有n，m≤100，ai，xi，yi绝对值不超过1000；
    　　对于60%的数据，有n，m≤1000，ai，xi，yi绝对值不超过100000；
    　　对于100%的数据，有n，m≤100000，ai，xi，yi绝对值不超过100000000。

    考虑三种情况：

    1：两个点在x轴同侧

    这个情况不用考虑，直接计算哈密顿距离即可。

    2.两个点在x轴异侧，且两点间有一个出口

    这个情况其实也可以直接计算，和1一模一样。

    3.两个点在x轴异侧，但是两点间没有出口

    这个情况就要找到某个出口，使得它离两点的x轴距离和最近。

    最后答案就是距离和。

    　　那么如何求出口位置?

    　　我的写法是用lowbit取点，如果两个点的lowbit一样，说明是第3种情况，否则是第2种，但计算答案3时也要特判一下在两点前面的那个出口。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int read(){
 4     int x=0,f=1;
 5     char c=getchar();
 6     while(!isdigit(c)){
 7         if(c=='-') f=-1;
 8         c=getchar();
 9     }
10     while(isdigit(c)){
11         x=(x<<1)+(x<<3)+(c^48);
12         c=getchar();
13     }
14     return x*f;
15 }
16 const int N=1e5+10;
17 int n,m,x1,y_1,x2,y2;
18 int a[N];
19 int main(){
20     
21     n=read();
22     for(int i=1;i<=n;i++) a[i]=read();
23     sort(a+1,a+n+1);
24     m=read();
25     for(int i=1;i<=m;i++){
26         x1=read();y_1=read();x2=read();y2=read();
27         int pos1=lower_bound(a+1,a+n+1,x1)-a;
28         int pos2=lower_bound(a+1,a+n+1,x2)-a;
29         if((y_1>0&&y2>0)||(y_1<0&&y2<0)){
30             printf("%d
",abs(y_1-y2)+abs(x1-x2));
31         }
32         else if(pos1==pos2){
33             printf("%d
",abs(y2-y_1)+min(abs(x1-a[pos1])+abs(x2-a[pos1]),abs(x1-a[pos1-1])+abs(x2-a[pos1-1])));
34         }
35         else{
36             printf("%d
",abs(x2-x1)+abs(y2-y_1));
37         }
38     }
39     return 0;
40 }

    Description

    【问题背景】
    　　2012年12月21日下午3点14分35秒，全世界各国的总统以及领导人都已经汇聚在中国的方舟上。
    　　但也有很多百姓平民想搭乘方舟，毕竟他们不想就这么离开世界，所以他们决定要么登上方舟，要么毁掉方舟。

    　　LHX教主听说了这件事之后，果断扔掉了手中的船票。在地球即将毁灭的那一霎那，教主自制了一个小型火箭，奔向了月球……

    　　教主登上月球之后才发现，他的女朋友忘记带到月球了，为此他哭了一个月。
    　　但细心的教主立马想起了小学学过的一篇课文，叫做《嫦娥奔月》，于是教主决定，让嫦娥做自己的新任女友。

    【题目描述】
    　　教主拿出他最新研制的LHX(Let's be Happy Xixi*^__^*)卫星定位系统，轻松地定位到了广寒宫的位置。
    　　见到嫦娥之后，教主用温柔而犀利的目光瞬间迷倒了嫦娥，但嫦娥也想考验一下教主。
    　　嫦娥对教主说：“看到那边的环形山了么？你从上面那个环走一圈我就答应你～”

    　　教主用LHX卫星定位系统查看了环形山的地形，环形山上一共有N个可以识别的落脚点，以顺时针1~N编号。每个落脚点都有一个海拔，相邻的落脚点海拔不同（第1个和第N个相邻）。
    　　教主可以选择从任意一个落脚点开始，顺时针或者逆时针走，每次走到一个相邻的落脚点，并且最后回到这个落脚点。
    　　教主在任意时刻，都会有“上升”、“下降”两种状态的其中一种。

    　　当教主从第i个落脚点，走到第j个落脚点的时候（i和j相邻）
    　　j的海拔高于i的海拔：如果教主处于上升状态，教主需要耗费两段高度差的绝对值的体力；否则耗费高度差平方的体力。
    　　j的海拔低于i的海拔：如果教主处于下降状态，教主需要耗费两段高度差的绝对值的体力；否则耗费高度差平方的体力。
    　　
    　　当然，教主可以在到达一个落脚点的时候，选择切换自己的状态（上升→下降，下降→上升），每次切换需要耗费M点的体力。在起点的时候，教主可以自行选择状态并且不算切换状态，也就是说刚开始教主可以选择任意状态并且不耗费体力。

    　　教主希望花费最少的体力，让嫦娥成为自己的女朋友。
     

    Input

    　　输入的第一行为两个正整数N与M，即落脚点的个数与切换状态所消耗的体力。
    　　接下来一行包含空格隔开的N个正整数，表示了每个落脚点的高度，题目保证了相邻落脚点高度不相同。

    Output

    　　输出仅包含一个正整数，即教主走一圈所需消耗的最小体力值。
    　　注意：C++选手建议使用cout输出long long类型整数。
     

    Sample Input

    6 7
4 2 6 2 5 6

    Sample Output

    27
     

    Data Constraint

     
     

    Hint

    【样例说明】
    　　从第3个落脚点开始以下降状态向前走，并在第4个落脚点时切换为上升状态。
    　　这样共耗费4 +(7)+3+1+2^2+2^2+4=27点体力。

    【数据规模】
    　　对于10%的数据，N ≤ 10；
    　　对于30%的数据，N ≤ 100，a[i] ≤ 1000；
    　　对于50%的数据，N ≤ 1000，a[i] ≤ 100000；
    　　对于100%的数据，N ≤ 10000，a[i] ≤ 1000000，M ≤ 1000000000；

    dp题。

    非常烦人的一道题目

    不写了。

    Description

    【问题背景】
    　　教主LHX作为知名人物，时刻会有恐怖分子威胁他的生命。于是教主雇佣了一些保镖来保障他的人生安全。

    【题目描述】
    　　教主一共雇佣了N个保镖，编号为1~N。每个保镖虽然身手敏捷武功高强，但是他在其余N-1个保镖里，都会有一个“上司”，他会对他的上司言听计从。但一号保镖例外，他武功盖世，不惧怕其余任何保镖，所以他没有上司。
    　　教主LHX会对这N个保镖进行定期视察。每次视察的时候，首先会让所有保镖排队。
    　　对于每个保镖，在他心目中会对他的所有下属的武功实力排个队。
    　　现在教主要求排出来的队伍满足：①互为上司-下属的两个保镖，上司在前，下属在后 ②对于一个保镖的所有下属，武功实力较强的在前，较弱的在后。
    　　教主想知道，总的排队方法数除以10007的余数是多少。
     

    Input

    　　输入的第一行为一个正整数T，表示了数据组数。
    　　对于每组数据：
    　　第一行为一个正整数N。
    　　接下来N行，每行描述一个保镖。
    　　第i+1行，会有一个整数K，代表第i个保镖的下属个数，接下来K个数，代表第i个保镖的下属按照武功实力从高到低的编号。

    Output

    　　输出包括C行，每行对于每组数据输出方案数mod 10007后的结果。
     

    Sample Input

    2
5
2 2 3
2 4 5
0
0
0
7
2 2 3
2 4 5
2 6 7
0
0
0
0

    Sample Output

    3
10
     

    Data Constraint

     
     

    Hint

    【样例说明】
    　　对于第1组数据，有以下3种排列是合法的：
    　　1 2 4 3 5
    　　1 2 3 4 5
    　　1 2 4 5 3
    　　同时满足了1在2与3之前且2在3之前，2在4与5之前且4在5之前

    【数据规模】
    　　对于20%的数据，有N ≤ 9；
    　　对于40%的数据，有对于所有K，有K ≤ 2；
    　　对于60%的数据，有N ≤ 100；
    　　对于100%的数据，有T ≤ 10，N ≤ 1000，K ≤ N。

    很有趣的一道题。

    题意满足一棵树的关系：

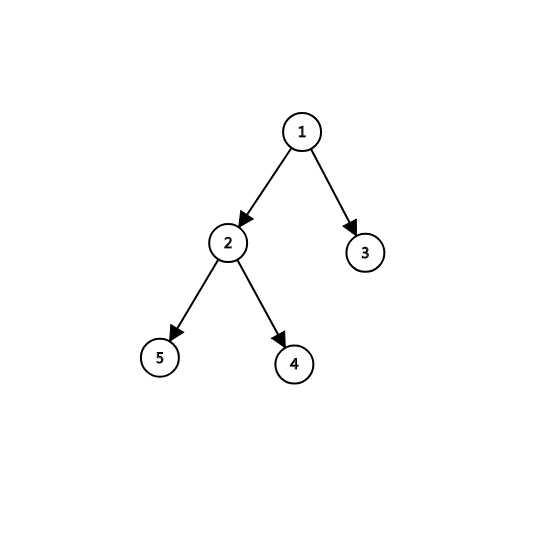
     样例的树长这样。

    一共有5个节点，那么我们有5！种排列，

    分别对每个节点讨论：

    点1要放在所有点前面，而将点1放在下方4个节点中，有5种放法。

     所以答案只取一种，故要除以5.

    对于每个点，我们知道它一定在它的所有子树，和与它同一层的后面的节点包括子树的前面。

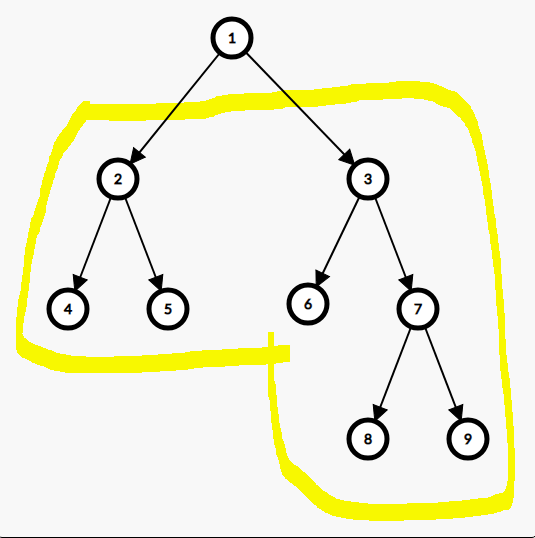
     比如对于这个图，2要放在圈起来的所有点的前面，因此要除以8。

    所以用邻接矩阵建图(用邻接表会打乱遍历的顺序)，然后处理当前情况下节点所在的排列大小，把所有答案的逆元乘起来，再乘上总点数的阶乘就能得到答案。

    即：

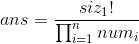
    num表示该点和能力比他弱的同层节点子树大小和。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int read(){
 4     int x=0,f=1;
 5     char c=getchar();
 6     while(!isdigit(c)){
 7         if(c=='-') f=-1;
 8         c=getchar();
 9     }
10     while(isdigit(c)){
11         x=(x<<1)+(x<<3)+(c^48);
12         c=getchar();
13     }
14     return x*f;
15 }
16 const int mod=10007;
17 const int N=2000;
18 int t,n,k,ans;
19 int siz[N];
20 int mul[N];
21 vector<int> edge[N];
22 int qp(int x,int y){
23     int res=x,aa=1;
24     while(y){
25         if(y&1) aa=(res*aa)%mod;
26         res=(res*res)%mod;
27         y>>=1;
28     }
29     return aa;
30 }
31 void dfs(int u){
32     siz[u]=1;
33     for(int i=0;i<edge[u].size();i++){
34         int v=edge[u][i];
35         dfs(v);
36         siz[u]=siz[u]+siz[v];
37     }
38 }
39 void dfs2(int u,int now){
40     for(int i=0;i<edge[u].size();i++){
41         int v=edge[u][i];
42         ans=(ans*qp(now,mod-2))%mod;
43         now-=siz[v];
44         dfs2(v,siz[v]-1);
45     }
46 }
47 int main(){
48     t=read();
49     mul[0]=1;
50     for(int i=1;i<=1500;i++)mul[i]=(mul[i-1]*i)%mod;
51     while(t--){
52         memset(edge,0,sizeof(edge));
53         n=read();
54         for(int i=1;i<=n;i++){
55             k=read();
56             for(int j=1;j<=k;j++){
57                 edge[i].push_back(read());
58             }
59         }
60         dfs(1);
61         ans=qp(siz[1],mod-2);
62         dfs2(1,siz[1]-1);
63         printf("%d
",(ans*mul[siz[1]])%mod);
64     }
65     return 0;
66 }

    Description

    【题目背景】
    　　LHX教主身为宇宙第一富翁，拥有一栋富丽堂皇的别墅，由于别墅实在太大了，于是教主雇佣了许许多多的人来负责别墅的卫生工作，我们不妨称这些人为LHXee。

    【题目描述】
    　　教主一共雇佣了N个LHXee，这些LHXee有男有女。
    　　教主的大别墅一共有M个房间，现在所有的LHXee在教主面前排成了一排。教主要把N个LHXee分成恰好M个部分，每个部分在队列中都是连续的一段，然后分别去打扫M个房间。
    　　教主身为全世界知识最渊博的人，他当然知道男女搭配干活不累的道理，以及狼多羊少，羊多狼少的危害之大。所以教主希望一个分配方式，使得所有小组男女个数差的最大值最小。
    　　教主还希望你输出从左到右，每个组的人数。
    　　如果有多种人数组合都能达到最优值，教主希望你分别告诉他这些方案中字典序最小和最大的方案。换句话说，你需要找到两种方案，这两种方案满足所有组男女个数差最大值最小的前提下，第一种方案（字典序最小）要越靠前的组人数越少，也就是让第一个小组人尽量少，并且在第一个小组人尽量少的前提下，让第二个小组的人尽量少，依此类推；第二种方案（字典序最大）则要让越靠前的组人数越多。
     

    Input

    　　输入的第1行为两个正整数N与M，用空格分隔。
    　　第2行包含一个长度为N的串，仅由字符组成，第i 个字符为0表示在这个位置上的LHXee为女生，若为1则为男生。

    Output

    　　输出文件包含两行，每行M个正整数，正整数之间用空格隔开，行末无多余空格。这M个正整数从左到右描述了你所分的每个组的人数。
    　　第1行为字典序最小的方案，第2行为字典序最大的方案。
     

    Sample Input

    8 3
11001100

    Sample Output

    1 2 5
5 2 1
     

    Data Constraint

     
     

    Hint

    【样例说明】
    　　字典序最小的方案按1, 10, 01100分组，每组男女个数差的最大值为1，为最小。
    　　字典序最大的方案按11001, 10, 0分组。

    【数据规模】
    　　对于40%的数据，有N ≤ 100；
    　　对于50%的数据，有N ≤ 1000；
    　　对于65%的数据，有N ≤ 100000；
    　　对于100%的数据，有N ≤ 5000000，M ≤ N且M ≤ 100000。

    【提示】
    关于字典序：
    比较S1[N]与S2[N]的字典序大小，可以找到S1[N]与S2[N]中第1个不相同数字S1[i]与S2[i]（即有对于所有1≤k＜i，都有S1[k] ＝S2[k]，但S1[i]≠S2[i]）。如果S1[i]＜S2[i]，那么说S1[N]字典序比S2[N]小，否则说S1[N]字典序比S2[N]大。

     吐槽一下这个题解：

     还是不要用语文来考验我们这些蒟蒻了吧。

    　　我的基本想法是，先求出最小差值，然后贪心就能得到字典序最小的方案，反过来再求一次就能得到字典序最大的方案。

    最小差值=S(n)/m,S(n)表示差值前缀和。

    考虑一种特殊情况：如果S(n)=0时，要看前缀和中有多少个0，如果0的数量大于分割数m，说明一定可以分成至少m份，每份大小为0，因此答案就是0，否则答案为1，因为至少有两份是将为0的某一份独立拆开的。

    最后一遍贪心就可以得到正解了。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=5e6+10;
 4 inline int read(){
 5     int x=0,f=1;
 6     char c=getchar();
 7     while(!isdigit(c)){
 8         if(c=='-') f=-1;
 9         c=getchar();
10     }
11     while(isdigit(c)){
12         x=(x<<1)+(x<<3)+(c^48);
13         c=getchar();
14     }
15     return x*f;
16 }
17 int n,m;
18 int sa[N],sb[N];
19 int c,d,ans1,ans2;
20 inline int gans(int r,int r_){
21     return r%r_==0?r/r_:(r/r_)+1;
22 }
23 int main(){
24     n=read();
25     m=read();
26     for(int i=1;i<=n;i++){
27         sa[i]=sb[n-i+1]=getchar()-'0';
28     }
29     int t1=0,t2=0;
30     for(int i=1;i<=n;i++){
31         sa[i]=sa[i-1]+(sa[i]==1?1:-1);
32         sb[i]=sb[i-1]+(sb[i]==1?1:-1);
33         if(sa[i]==0) t1++;
34         if(sb[i]==0) t2++;
35     }
36     if(sa[n]==0){
37         if(t1>=m);
38         else c=1;
39     } 
40     else c=gans(abs(sa[n]),m);
41     
42     if(sb[n]==0){
43         if(t2>=m);
44         else d=1;
45     } 
46     else d=gans(abs(sb[n]),m);
47     int num=m;
48     int p=0;
49     for(int i=1;i<=n;i++){
50         if(abs(sa[i]-sa[p])<=c&&gans(abs(sa[n]-sa[i]),num-1)<=c){
51             printf("%d ",i-p);
52             num--;
53             p=i;
54             if(num==1) break;
55         }
56     }
57     printf("%d
",n-p);
58     num=m;
59     p=0;
60     int cnt=0;
61     for(int i=1;i<=n;i++){
62         if(abs(sb[i]-sb[p])<=d&&gans(abs(sb[n]-sb[i]),num-1)<=d){
63             sa[++cnt]=i-p;
64             num--;
65             p=i;
66             if(num==1) break;
67         }
68     }
69     printf("%d ",n-p);
70     for(int i=cnt;i>=1;i--) printf("%d ",sa[i]);
71     return 0;
72 }
    ——抓住了时间，却不会利用的人，终究也逃不过失败的命运。
  • 相关阅读:
    Delphi 枚举所有进程
    从零开始学JAVA(07)-使用SpringMVC4写helloworld
    Delphi下OpenGL2d绘图(06)-画图(多窗口、多视图、多个DC）
    Delphi下OpenGL2d绘图(05)-画图片Bmp
    Delphi下OpenGL2d绘图(04)-画四边形
    Windows下重置MySQL密码【MYSQL】
    HTML5 WEB Storage
    相关转载
    基本的查询流【MSSQL】
    查询编辑器便捷特性【MSSQL】
  • 原文地址：https://www.cnblogs.com/Nelson992770019/p/11625449.html
Copyright © 2020-2023  润新知