多层神经网络
对于多层神经网络的训练，delta规则是无效的，因为应用delta规则训练必须要误差，但在隐含层中没有定义。输出节点的误差是指标准输出和神经网络输出之间的差别，但训练数据不提供隐藏层的标准输出。
真正的难题在于怎么定义隐藏节点的误差，于是有了反向传播算法。反向传播算法的重要性在于，它提供了一种用于确定隐含节点误差的系统方法。在该算法中，输出误差从输出层逐层后移，直到与输入层相邻的隐含层。
1.反向传播算法
在反向传播算法中，隐含节点误差的计算方式是求取delta的反向加权和，节点的delta是误差与激活函数导数之积。该过程从输出层开始，并重复于所有隐含层。
MATLAB代码实现：
输入数据为 { [(0,0,1),0],[(0,1,1),1],[(1,0,1),1],[(1,1,1),0] }，网络结构为三个输入节点，四个节点组成的隐含层，一个输出节点。Sigmoid函数为激活函数，采用SGD实现反向传播算法。
function [W1, W2] = BackpropXOR(W1, W2, X, D)
% 以神经网络的权重和训练数据作为输入，返回调整后的权重
% 其中W1和W2为相应层的权重矩阵；X和D分别是训练数据的输入和标准输入
alpha = 0.9;
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v1 = W1*x;
y1 = Sigmoid(v1);
v = W2*y1;
y = Sigmoid(v);
e = d - y;
delta = y.*(1-y).*e;
e1 = W2'*delta; % 反向传播
delta1 = y1.*(1-y1).*e1;
dW1 = alpha*delta1*x';
W1 = W1 + dW1;
dW2 = alpha*delta*y1';
W2 = W2 + dW2;
end
end
Sigmoid函数定义如下：
function y = Sigmoid(x)
y = 1 ./ (1 + exp(-x));
end
验证函数效果程序：
clear all
X = [ 0 0 1;
0 1 1;
1 0 1;
1 1 1;
];
D = [ 0
1
1
0
];
W1 = 2*rand(4, 3) - 1;
W2 = 2*rand(1, 4) - 1;
for epoch = 1:10000 % train
[W1 W2] = BackpropXOR(W1, W2, X, D);
end
N = 4; % inference
for k = 1:N
x = X(k, :)';
v1 = W1*x;
y1 = Sigmoid(v1);
v = W2*y1;
y = Sigmoid(v)
end
输出结果为：0.0077，0.9887，0.9885，0.0134。解决了异或问题。
2.动量
动量m是一个添加到delta规则中用于调整权重的项。使用动量项推动权重在一定程度上向某个特定方向调整，而不是产生立即性改变。它的行为类似于物理学中的动量，能够阻碍物体本身对外力的反应。
是上一次的动量，
是一个小于1的常数。动量随时间变化方式如下：
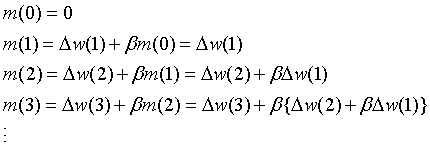
在过程的每一步，都向动量加上上一步的权重更新，如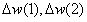
等。由于小于1，所以越早的权重更新对动量的影响越小。虽然影响力随着时间的推移而减弱，但是更早的权重更新仍然存在于动量之中。因此，权重不仅受某个特定权重更新值的影响。故而，学习的稳定性得到提高。此外，动量随着权重更新而逐渐增大。因而权重更新量也随之越来越大。因此，学习的效率也提高了。
应用了动量的反向传播算法：
function [W1, W2] = BackpropMmt(W1, W2, X, D)
alpha = 0.9;
beta = 0.9;
mmt1 = zeros(size(W1));
mmt2 = zeros(size(W2));
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v1 = W1*x;
y1 = Sigmoid(v1);
v = W2*y1;
y = Sigmoid(v);
e = d - y;
delta = y.*(1-y).*e;
e1 = W2'*delta;
delta1 = y1.*(1-y1).*e1;
% 动量
dW1 = alpha*delta1*x';
mmt1 = dW1 + beta*mmt1;
W1 = W1 + mmt1;
dW2 = alpha*delta*y1';
mmt2 = dW2 + beta*mmt2;
W2 = W2 + mmt2;
end
end
测试代码：
clear all
X = [ 0 0 1;
0 1 1;
1 0 1;
1 1 1;
];
D = [ 0
1
1
0
];
W1 = 2*rand(4, 3) - 1;
W2 = 2*rand(1, 4) - 1;
for epoch = 1:10000 % train
[W1 W2] = BackpropMmt(W1, W2, X, D);
end
N = 4; % inference
for k = 1:N
x = X(k, :)';
v1 = W1*x;
y1 = Sigmoid(v1);
v = W2*y1;
y = Sigmoid(v)
end
测试结果为 0.0030，0.9947，0.9909，0.0160。
3.代价函数与学习规则
神经网络误差的度量就是代价函数。神经网络的误差越大，代价函数的值就越高。
交叉熵函数对误差更敏感，通常认为交叉熵函数导出的学习规则能够得到更好的性能。正则化的本质是将权重叠加到代价函数中
。
交叉函数示例程序：网络结构和输入数据更上面一样
function [W1, W2] = BackpropCE(W1, W2, X, D)
alpha = 0.9;
N = 4;
for k = 1:N
x = X(k, :)'; % x = a column vector
d = D(k);
v1 = W1*x;
y1 = Sigmoid(v1);
v = W2*y1;
y = Sigmoid(v);
e = d - y;
delta = e;
e1 = W2'*delta;
delta1 = y1.*(1-y1).*e1;
dW1 = alpha*delta1*x';
W1 = W1 + dW1;
dW2 = alpha*delta*y1';
W2 = W2 + dW2;
end
end
其差别在于delta的计算上。以下是测试代码：
clear all
X = [ 0 0 1;
0 1 1;
1 0 1;
1 1 1;
];
D = [ 0
1
1
0
];
W1 = 2*rand(4, 3) - 1;
W2 = 2*rand(1, 4) - 1;
for epoch = 1:10000 % train
[W1 W2] = BackpropCE(W1, W2, X, D);
end
N = 4; % inference
for k = 1:N
x = X(k, :)';
v1 = W1*x;
y1 = Sigmoid(v1);
v = W2*y1;
y = Sigmoid(v)
end
输出结果为 4.0043e-05，0.9997，0.9999，3.9127e-04。
4.代价函数比较
比较两种代价函数的误差均值，代码如下：
clear all
X = [ 0 0 1;
0 1 1;
1 0 1;
1 1 1;
];
D = [ 0
0
1
1
];
E1 = zeros(1000, 1);
E2 = zeros(1000, 1);
W11 = 2*rand(4, 3) - 1; % Cross entropy
W12 = 2*rand(1, 4) - 1; %
W21 = W11; % Sum of squared error
W22 = W12; %
for epoch = 1:1000
[W11 W12] = BackpropCE(W11, W12, X, D);
[W21 W22] = BackpropXOR(W21, W22, X, D);
es1 = 0;
es2 = 0;
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v1 = W11*x;
y1 = Sigmoid(v1);
v = W12*y1;
y = Sigmoid(v);
es1 = es1 + (d - y)^2;
v1 = W21*x;
y1 = Sigmoid(v1);
v = W22*y1;
y = Sigmoid(v);
es2 = es2 + (d - y)^2;
end
E1(epoch) = es1 / N;
E2(epoch) = es2 / N;
end
plot(E1, 'r')
hold on
plot(E2, 'b:')
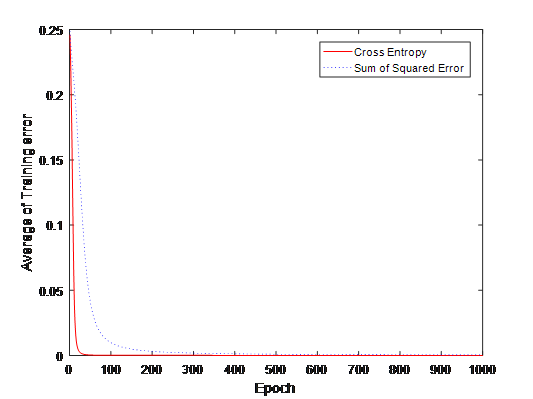
xlabel('Epoch')
ylabel('Average of Training error')
legend('Cross Entropy', 'Sum of Squared Error')
输出结果下图所示，交叉熵代价函数能更快地速度降低训练误差。
