题目链接
IPSC 2011 Problem I – Inverting bits
题目大意
你有 (26) 个变量 (A-Z),每个变量初始为 (0),可以存储一个 (8) 位无符号整数,你可以对它们做「 赋值、按位与、按位或、取反、左移、右移、读入、输出」 (8) 种操作,运算中可以使用数字常量。
现在你要读入 (n) 个 (0/1) 值,将它们 flip 之后按序输出,并且不得使用超过 (k) 次取反操作。
Easy Subproblem: (n=7,k=1)
Hard Subproblem: (n=19,k=2)
思路
Easy Subproblem 把 (7) 个数字塞到一个变量的前 (7) 个二进制位上取反后拆回来输出即可。
Hard Subproblem 相对难一些,有一个直观但延展性差的做法和一个抽象但潜力巨大的做法。
(n=19) 很有迷惑性,两个做法都是把它们塞到 (3) 个 (8) 位整数中然后取反的。
法一
把每个数字看作一个集合,由二进制上为 (1) 的位置组成,于是「按位与、按位或和取反」就变成了「取交集、取并集、和全局取补集」的集合操作,把维恩图画出来:
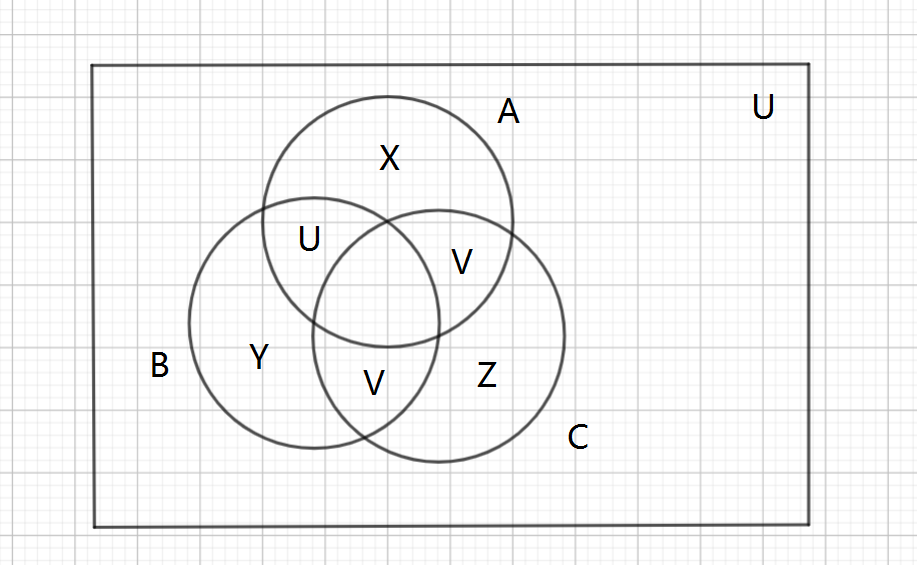
(好像重名了,emmm反正全集用不上不改了)
我们设 (E) 为中间三叶草形状的区域:
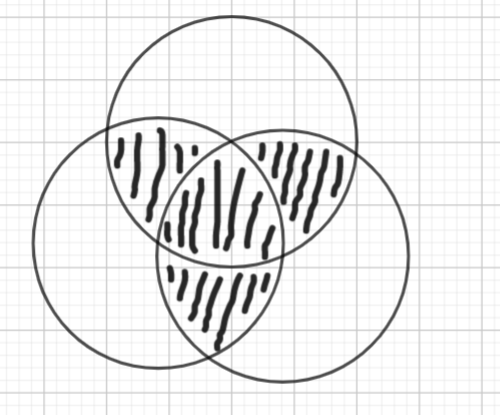
简洁起见用 (AB) 表示 (Acap B),(A+B) 表示 (Acup B),(overline A) 表示 (complement_U A),则 (E=AB+BC+CA) .
对 (E) 取反,可以发现可以算出 (X=overline EA,Y=overline EB,Z=overline EC),利用这个,我们再构造一个图形 (F) :
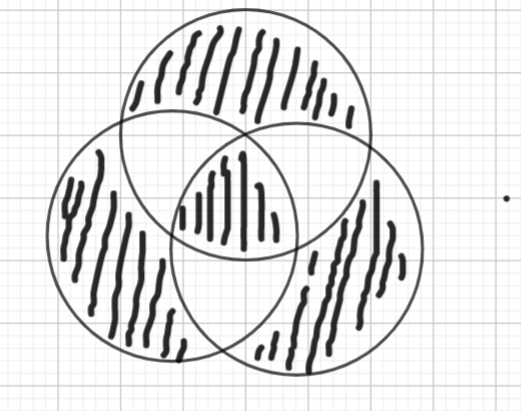
(F=X+Y+Z+ABC),而 (overline F) 很有用,通过它可以得到 (U=overline FAB,V=overline FBC,W=overline FCA),然后我们所需要的信息基本就全了,可以发现原来要求的反即两个扇形((X/Y/Z))和一个三叶草的叶子((U/V/W))以及外面的补集组成,而外面的补集即 (overline Foverline E),所以就做完了:
(overline A=overline E overline F+Y+Z+W),(overline B=overline E overline F+X+Z+V),(overline C=overline E overline F+X+U+Y) 。
这个做法基本上属于利用了数据小的特点,瞎试出来的,拓展到一般情况很困难,毕竟大小为 (4) 的维恩图就已经比较难画了,因此一般情况需要另一个做法。
法二
题解思路,由于把 (0/1) 值塞到 (8) 位整数里是纯技术问题,下面的 (n) 是题面中的 (lceilfrac{n}{8} ceil) 。
我们的操作中不包含条件语句,所以需要一种全局性的方法去解决所有情况,注意到二进制的每一位之间是互不干扰的,所以可以分开来考虑,要求我们的做法对于任意一位上的 (0/1) 排列都能进行翻转,问题便转化为翻转 (n) 个 (0/1) 值。
注意到问题的本质就是当一位是 (1) 时,将它变为 (0),反之变为 (1),所以操作需要区分 (0) 和 (1),那么可以这样区分:假设对于 (iin[0,n]),我们知道 (ex(i)) 的真假情况,即 (n) 个值中是否恰好有 (i) 个 (1),,那么当前值 (a_i) 翻转后的值可以表示为:
其中 (And(S)) 和 (Or(S)) 分别表示集合 (S) 中所有元素的「与和」跟「或和」,若 (a_i) 在那若干个 (1) 中,则式子为 (0),否则为 (1) 。于是现在的问题便转化成了如何在 (2) 次取反操作内,得到 (ex(0)) 到 (ex(3)),注意到 (ex(i)=[one(all)geq i]&[one(all)leq i]),于是引入 (lst(i)=[one(all)geq i],mst(i)=[one(all)leq i]),容易发现:
经过一定的思考便可以得到原题的解法了:
第 (5) 步的手法很奇妙,我们把它拓展一下,开始我们先用一次取反得到 (mst(mid)),可以发现 ([0,mid]) 和 ([mid+1,n]) 变成了和原来相同的子问题,注意原来的 (mst(n)) 没啥用,它必然为 (1),但是在子问题中右端点的 (mst) 很有用,并且在求 (mst(mid)) 的时候已经得到了。
使用全局分治的思路,在求下一层分治的 (mst(mid)) 的时候,我们直接求出所有 (mid) 位置 (mst) 的或,可以发现即 (sim And({lst(i+1)|iin{ ext{下一层的mid}}})),这个值再与上 (mst(r)) 即为 (mst(mid)) 了,这样递归总共有 (lceil log_2 (n+1) ceil) 层,每层只需要使用一次取反,所以使用这种方法,取反 (n) 个数字只需要至多 (lceil log_2 (n+1) ceil) 次取反操作即可。
不大会证这是否是下界,但应该也算是比较优秀的做法了吧。