题目链接:P1912 [NOI2009]诗人小G
题目大意:
给定 (N) 句诗和行标准长度 (L) ,定义一行长度为 (S) 的诗(包含空格等符号的总个数)的不协调度为 (|L-S|^P) ,要求输出一种排版方案,使得每句诗都完整地在一行上,句与句之间以空格分隔,并且所有行的不协调度的和最小。
(Nleq 10^5) , (Lleq3*10^6) , (Pleq10) ,每句诗的字符数 (leq30)
思路:
令 (F[i]) 为前 (i) 句诗的最小不协调度,(sum[i]) 为前 (i) 句诗的长度和,则有朴素 (O(N^2)) DP:
( (i-j-1) 为空格个数),考虑对DP进行优化,记 (val(j,i)=|sum[i]-sum[j]+i-j-1-L|^P) ,观察这个式子有没有特殊性质,将 (val(j,i)) 写成 (|(sum[i]+i)-(sum[j]+j)-1-L|) ,(sum[i]+i) 是一个关于 (i) 单调递增的式子,由于 (val(j,i)) 有不定的高次指数 (P) ,不适合用单调队列或斜率优化,考虑 (val(i,j)) 是否满足四边形不等式:
记 (u=val(j,i),v=val(j+1,i)) ,由于前缀和的递推关系,记 (a[i]) 为第 (i) 句诗的长度,不等式可转化为
由于 (u>v),该式等价于证对于任意常数 (c) ,函数 (f(x)=|x|^P-|x-c|^P) 单调递减,这个式子可以通过导数很容易地证明(其实是我不想写了),放到Geogebra上可以感性地理解一下其正确性
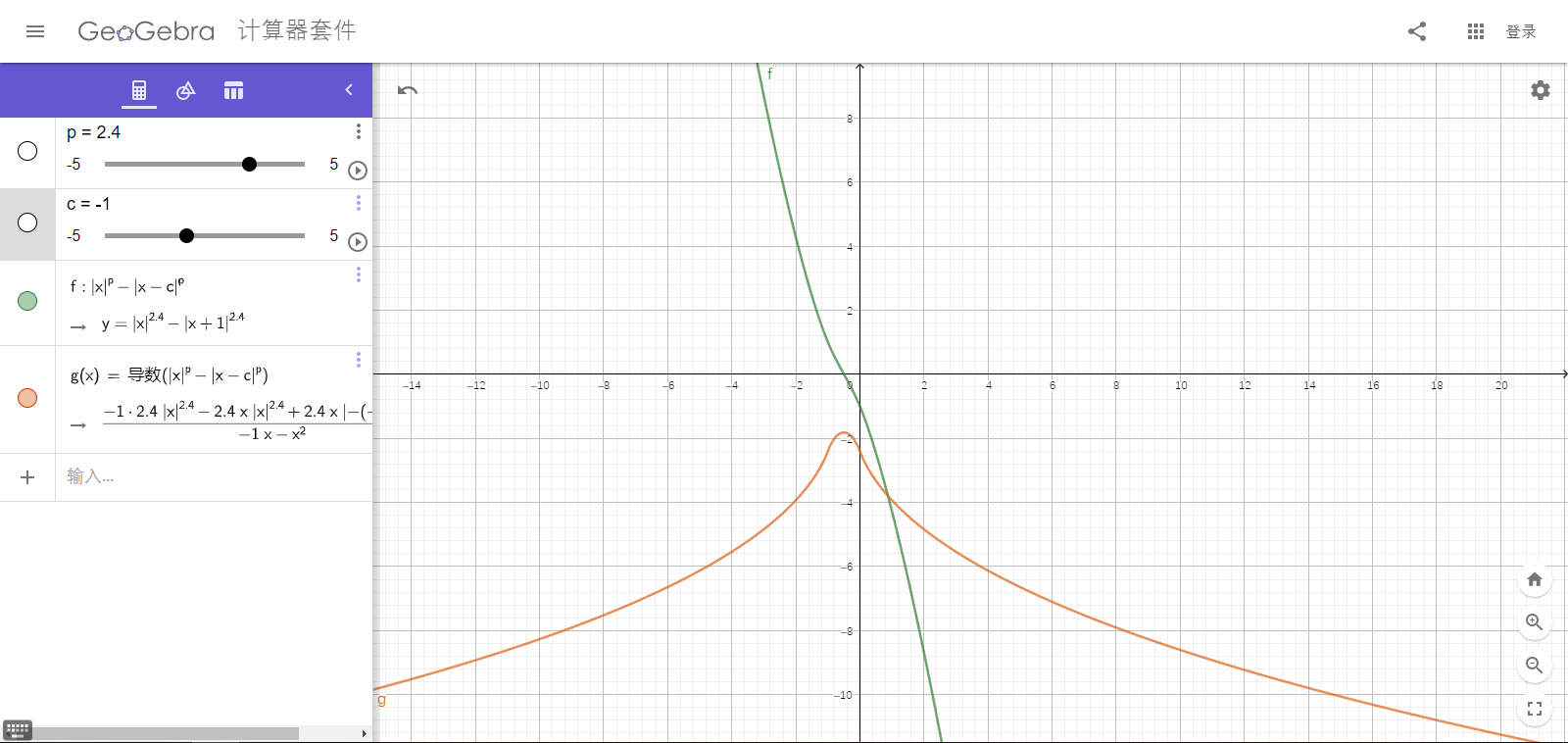
知道 (val(j,i)) 满足四边形不等式后,我们就可以得到 (F[x]) 具有决策单调性,用队列维护决策三元组,能够 (O(NlogN)) 解决本题。
实现细节:
- 题目要求在答案超过 (10^{18}) 的时候输出"Too hard to arrange",由于这个值long long也可能存不下,(F) 数组的类型要开成long double。
- 实现决策单调性DP的时候由于后面要统计方案,队头决策的左端点在被修改后要及时还原,同时插入决策前先判断其左右区间是否合法。
- 这道题我被卡常了,注意输出排版的时候尽量不要用递归,将决策队列处理成分段方式存在数组里后循环输出,另外请手写快速幂,cmath的pow太慢了容易TLE。
- 每一行诗的结尾不要留空格
Code:
#pragma optimize(O3)
#include<iostream>
#include<cstdio>
#include<cmath>
#include<fstream>
#include<cstring>
#define ll long long
#define ld long double
#define N 100100
#define RG register
using namespace std;
struct choise{
int i,l,r;
}q[N];
ld dp[N],sum[N],L;
int T,n,p,l,r,out[N];
char s[N][35];
void _printf(string s){
int k=s.size();
for(register int i=0;i<k;i++)putchar(s[i]);
}
inline ld qpow(RG ld a,RG int b){
RG ld ret=1;
for(;b;b>>=1){
if(b&1)ret*=a;a*=a;
}
return ret;
}
inline ld val(RG int j,RG int i){
return qpow(abs(sum[i]-sum[j]+i-j-1-L),p);
}
inline bool better(int a,int b,int i){
return dp[a]+val(a,i)<=dp[b]+val(b,i);
}
inline int binary_search(int l,int r,int a,int b){
RG int L=l,R=r;
while(L<R){
int mid=(L+R)>>1;
if(better(a,b,mid))R=mid;
else L=mid+1;
}
return L;
}
int main(){
int pos,temp;
cin>>T;
while(T--){
cin>>n>>L>>p;
for(int i=0;i<n;i++){
scanf("%s",s[i]);
sum[i+1]=sum[i]+strlen(s[i]);
}
l=r=0,q[0]={0,1,n};
for(int i=1;i<=n;i++){
while(l<=r&&q[l].r<i)l++;
temp=q[l].l,q[l].l=i;
dp[i]=dp[q[l].i]+val(q[l].i,i);
pos=n+1;
while(l<=r&&better(i,q[r].i,q[r].l))pos=q[r--].l;
if(l<=r&&better(i,q[r].i,q[r].r))
pos=binary_search(q[r].l,q[r].r,i,q[r].i);
if(l<=r)q[r].r=pos-1,q[l].l=temp;
if(pos<=n)q[++r]={i,pos,n};
}
if(dp[n]>1e18)cout<<"Too hard to arrange
";
else{
cout<<(ll)dp[n]<<endl;
int up=r;
temp=0,out[0]=n;
while(out[temp]){
while(up>=0&&q[up].l>out[temp])up--;
out[++temp]=q[up].i;
}
for(int i=temp;i>=1;i--){
for(int j=out[i];j<out[i-1];j++){
_printf(s[j]);
if(j!=out[i-1]-1)putchar(' ');
}
putchar('
');
}
}
puts("--------------------");
}
return 0;
}