1. 使用循环和向量化两种不同的方法来计算 100 以内的质数之和。
先定义个判断质数的函数。ps:纯手工打造,原生态,哈哈。
def checkprime(x):
if x<=1:
return False;
prime=True;
for i in range(2 , 1+x/2):
if x%i == 0:
prime = False;
break;
return prime;
使用循环方法来计算 100 以内的质数之和。
def sumprimebyiter(n=100):
primesum=0
for i in range(1, n+1):
if( True == checkprime(i)):
primesum += i
return primesum
%timeit sumprimebyiter(100)
10000 loops, best of 3: 138 µs per loop
使用向量化的方法来计算 100 以内的质数。ps:怎么将判断质数的函数应用到向量中的每一个元素,可是花了好几分钟来寻找,终于发现 map 可以实现这个功能。后来又发现 np.vectorize 也可以实现同样功能。
import numpy as np
def sumprimebyarr(n=100):
a = np.arange(1,n+1)
# return sum(a[np.array(map(CheckPrime, a))]) # 此处是之前用 Python 自带的 map 把函数应用到向量的每个元素
check_prime_vec = np.vectorize(CheckPrime) # 此处代码用到了 np.vectorize,可以把外置函数应用到向量的每个元素
return np.sum(a[check_prime_vec(a)])
%timeit sumprimebyarr(100)
10000 loops, best of 3: 204 µs per loop
上面两种方法都使用魔术函数 %timeit 计算了执行时间,意外的是,向量化的方法竟然没有循环快,一定是哪儿不对,待我好好检查下,再补充该题答案。
2. 模拟一个醉汉在二维空间上的随机漫步。
先试试一维空间上的随机漫步。既然本周学了 Numpy,这里就直接上 np.random 了。
%pylab inline
Populating the interactive namespace from numpy and matplotlib
nsteps = 1000
draws = np.random.randint(-1,2,size=nsteps)
walk = draws.cumsum()
plot(walk)
[<matplotlib.lines.Line2D at 0x7f52c3534250>]

再来看下二维的。
nsteps = 1000
draws = np.random.randint(-1,2,size=(2,nsteps))
walks = draws.cumsum(1)
plot(walks[0,:],walks[1,:])
[<matplotlib.lines.Line2D at 0x7f52c34cf3d0>]
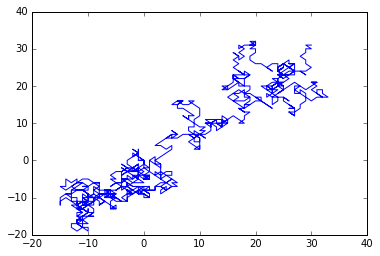
先生成 1000 个随机漫步方向,方向是从 {-1, 0, 1} 中随机挑两个值(两个值也可相等)作为移动方向,所以每次移动有 3×3=9 种选择,初始位置也是 9 种选择,cumsum 函数是将每次的移动累加,最后通过 plot 画出来。
代码调通之前,我都没想到代码能这么少。Python 还是好用,这要是用 C++ 写,得多少代码啊。
3. 使用梯形法计算一个二次函数的数值积分。
梯形法计算数值积分,就是把自变量分成无数小段,每一小段的面积用一个梯形面积近似,当小段的个数无限多,小段的长度无限小时,所有的小梯形面积加起来,就近似等于该函数的数值积分。如下图所示:
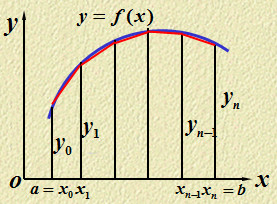
原理很简单,代码也很简单:
import numpy as np
def CompIntegralbyladder(func,x0,x1):
wholearea = 0
step = 0.1
for i in np.arange(x0, x1, step):
wholearea += (func(i)+func(i+step))*step/2; # Compute the Trapezoidal area
return wholearea;
该函数可以计算任意函数的积分。函数写好了,都分隔成长度为 0.1 的小区间。先来测试下指数函数的积分。
CompIntegralbyladder(np.exp,1,4)
51.923094224367127
来看下正确答案。注意指数函数的不定积分还是指数函数本身。
from sympy.interactive import printing
printing.init_printing(use_latex=True)
np.exp(4)-np.exp(1)
51.879868204685188
附上指数函数的图形。
%pylab inline
Populating the interactive namespace from numpy and matplotlib
import numpy as np
x = np.linspace(-5, 5, num = 100)
y = np.exp(x)
import matplotlib.pyplot as plt
plt.plot(x,y)
plt.show()

再看看计算个二次函数的积分。随便写个二次函数。
def Quadratic(x):
return 2*x**2 + 3*x + 4
先来看看这个函数的图形。
import numpy as np
x = np.linspace(-5, 5, num = 100)
y = Quadratic(x)
import matplotlib.pyplot as plt
plt.plot(x,y)
plt.show()

我们就计算该二次函数从 -5 到 5 的积分吧。
CompIntegralbyladder(Quadratic,-5,5)
206.69999999999825
下面来计算下正确的积分值。
因为:
所以:
def Integral(x):
return (2*x**3)/3 + (3*x**2)/2 + 4*x
Integral(5)-Integral(-5)
207
可见,梯形法计算积分还是比较准确的。