1. 离散节点
在官方Tutorial中是有详细的案例的,就是B篇3.3节,你可以动手把天气预报这个实现一下:
http://www.norsys.com/tutorials/netica/secB/tut_B3.htm#LearningProbTables

2. 连续节点
假如我想输入的不是离散的状态,而是连续的数值,则不能像上一个案例一样做了。
* 离散状态:难,易;阴,晴,雨;是,否……这些都是多选一问题,天气只能是“阴,晴,雨”三选一,课程难度只有“难,易”两个选项,而不是“0为最易10为最难下,难度系数为5.312...”。
* 连续数值:房屋的面积,平均房间数(因为是平均房间所以可以是4.6这样的数而非整数)。仍然以最简单的贝叶斯网A→B为例,A为房屋面积,B为房价,则A可以是连续的数值。
Netica对连续节点的处理是:划分区间,看给定的连续数值落在哪个区间内。这一操作被称之为“离散化”。怎么理解离散化呢,这让我想起几年前学习正态分布的时候网上提供的可视化程序均是通过绘制柱状图,而柱状图划分的越细,就越接近连续状态下的正态分布曲线。

下面给一个简单的案例,波士顿房价,其中网络结构由自己搭建(箭头的指向自定义),节点之间的关联采取“从数据中学习”的方式获得(本质上是从数据中学习CPT,数据来源:波士顿房价数据集(Boston House Price Dataset)(下载地址:http://t.cn/RfHTAgY),简化起见,在此我挑选了一氧化氮浓度、犯罪率以及平均房间数这三列)。
step 1: 把这个数据粘贴到txt文件中。
// ~->[CASE-1]->~
crime air room price
0.00632 0.5380 6.5750 24.00
0.02731 0.4690 6.4210 21.60
0.02729 0.4690 7.1850 34.70
0.03237 0.4580 6.9980 33.40
0.06905 0.4580 7.1470 36.20
0.02985 0.4580 6.4300 28.70
0.08829 0.5240 6.0120 22.90
0.14455 0.5240 6.1720 27.10
0.21124 0.5240 5.6310 16.50
0.17004 0.5240 6.0040 18.90
0.22489 0.5240 6.3770 15.00
step 2: 载入txt文件,自动生成节点,并且在弹出的对话框中指定“离散成多少个区间”。

step 3: 根据大致的因果关系手动连接节点构建网络。
step 4: 再次载入同一个txt文件以学习节点与节点之间的关联。

本质上所学习到的就是条件概率表(CPT)。
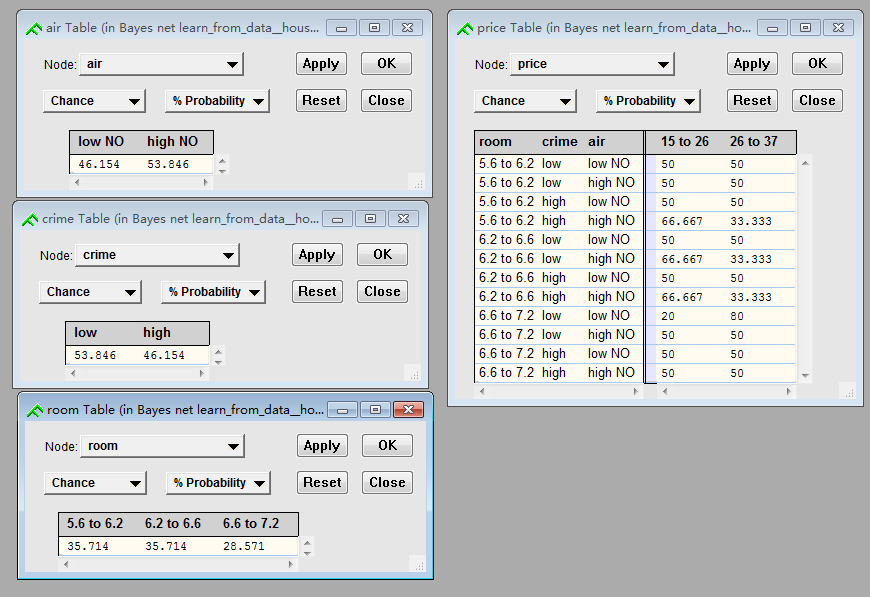
现在整个贝叶斯网就搭建好了。各个节点均为连续节点,也就是说我在获取新数据的时候,可以直接输入新数据(如:air=0.49):
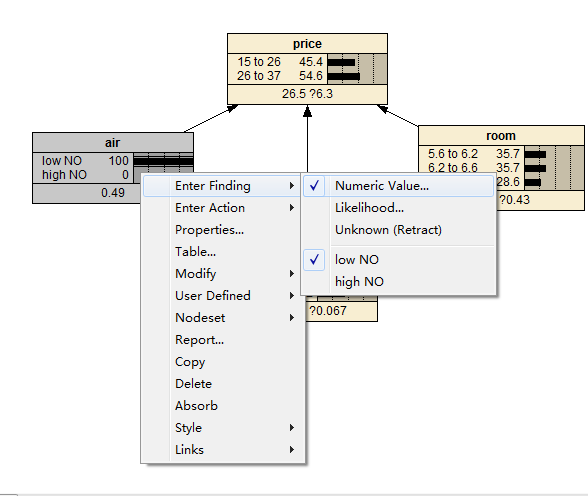
然后根据数值所属区间,Netica会自动给你归入到low NO或high NO(总感觉和想象的有点不一样,这样略粗糙啊,不过这就是Netica的设定)。
现在对搭建好的网络玩一下。可以发现将air调到“NO浓度最小”,crime调到“犯罪率最低”,room调到“房间数最多”的时候,房价属于“高房价区间”的可能性是最大的,这符合人类的基本认知。

2018.9.26
by 悠望南山