不论是利用Mayavi还是matplotlib绘制三维图表,里面都用到了numpy中的一个函数叫mgrid。本次博客我简单地讲一下mgrid是干什么用的,以及一个三维曲面是如何绘制出来的。
首先说明一下这里的三个变量分别是k(x轴)、b(y轴)以及ErrorArray(z轴)。为了更好地理解mgrid后的k、b以及ErrorArray是什么,我想在这里举个简单的例子,然后用Python做个图,这样大家就都明白了。
这次也不让Err=∑{i=1~n}([yi-(k*xi+b)]**2)了,来个简单的吧,假设f(k,b)=3k^2+2b+1,k轴范围为1~3,b轴范围为4~6:
【step1:k扩展】(朝右扩展):
[1 1 1]
[2 2 2]
[3 3 3]
【step2:b扩展】(朝下扩展):
[4 5 6]
[4 5 6]
[4 5 6]
【step3:定位(ki,bi)】(把上面的k、b联合起来):
[(1,4) (1,5) (1,6)]
[(2,4) (2,5) (2,6)]
[(3,4) (3,5) (3,6)]
【step4:将(ki,bi)代入f(k,b)=3k^2+2b+1求f(ki,bi)】
[12 14 16]
[21 23 25]
[36 38 40]
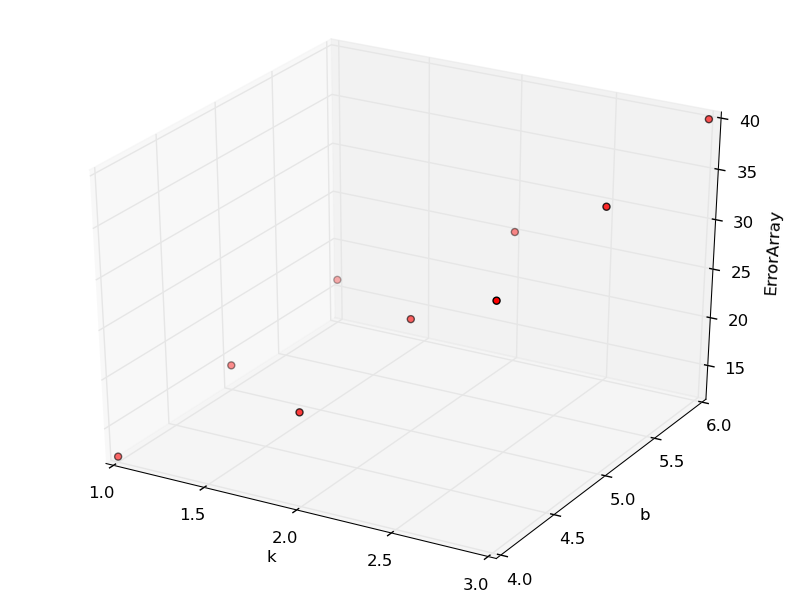
这部分代码如下:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import mpl_toolkits.mplot3d 4 import pylab as p 5 import mpl_toolkits.mplot3d.axes3d as p3 6 7 k,b=np.mgrid[1:3:3j,4:6:3j] 8 f_kb=3*k**2+2*b+1 9 10 k.shape=-1,1 11 b.shape=-1,1 12 f_kb.shape=-1,1 #统统转成9行1列 13 14 fig=p.figure() 15 ax=p3.Axes3D(fig) 16 ax.scatter(k,b,f_kb,c='r') 17 ax.set_xlabel('k') 18 ax.set_ylabel('b') 19 ax.set_zlabel('ErrorArray') 20 p.show()
【step5:将(ki,bi,f(ki,bi))连起来,形成曲面】
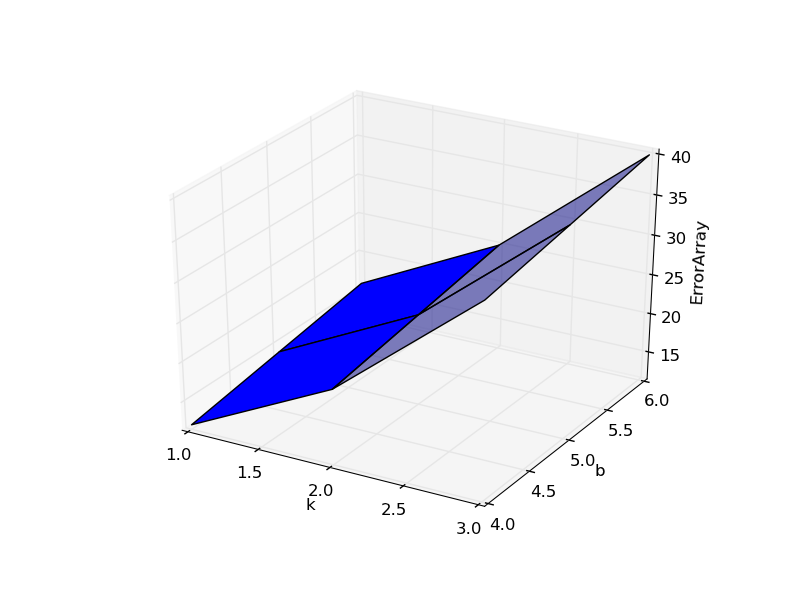
这部分代码如下:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import mpl_toolkits.mplot3d 4 import pylab as p 5 import mpl_toolkits.mplot3d.axes3d as p3 6 7 k,b=np.mgrid[1:3:3j,4:6:3j] 8 f_kb=3*k**2+2*b+1 9 10 ax=plt.subplot(111,projection='3d') 11 ax.plot_surface(k,b,f_kb,rstride=1,cstride=1) 12 ax.set_xlabel('k') 13 ax.set_ylabel('b') 14 ax.set_zlabel('ErrorArray') 15 p.show()
【其它说明】
上面讲了一种简单到夸张的情况,不过我认为很好的理解了mgrid。事实上当Err=∑{i=1~n}([yi-(k*xi+b)]**2)时也是同样的道理(这是最小二乘法拟合y=kx+b时的误差矩阵)。
mgrid中第三个参数越大,说明某一区间被分割得越细,相应的曲面越精准。在上面的例子中第三个参数为3j,如果说我们其它不变,单纯将参数改成10j,则曲面图如下:
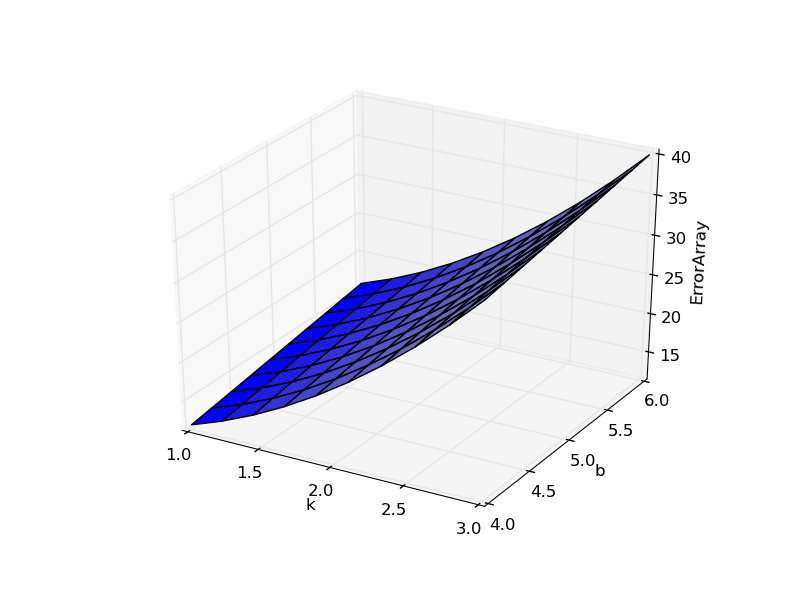
将参数改一下改成30j,则曲面图如下:
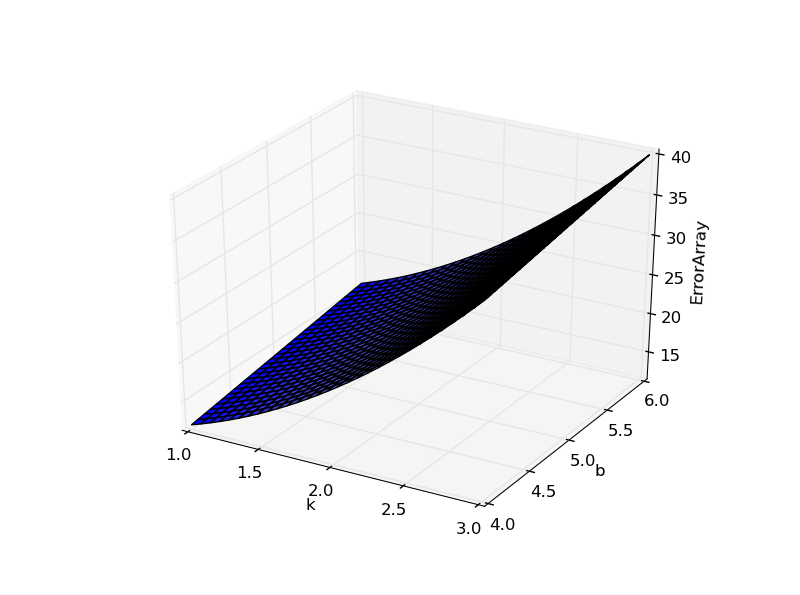
可以发现曲面变得非常柔和。
这部分代码如下:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import mpl_toolkits.mplot3d 4 import pylab as p 5 import mpl_toolkits.mplot3d.axes3d as p3 6 7 k,b=np.mgrid[1:3:30j,4:6:30j] 8 f_kb=3*k**2+2*b+1 9 10 ax=plt.subplot(111,projection='3d') 11 ax.plot_surface(k,b,f_kb,rstride=1,cstride=1) 12 ax.set_xlabel('k') 13 ax.set_ylabel('b') 14 ax.set_zlabel('ErrorArray') 15 p.show()
2016.4.3
by 悠望南山