Description
如图所示为某生态系统的食物网示意图,据图回答第1小题.
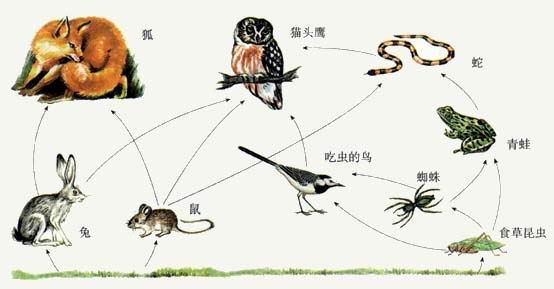
1.数一数,在这个食物网中有几条食物链( )
现在给你n个物种和m条能量流动关系,求其中的食物链条数。
物种的名称为从1到n编号
M条能量流动关系形如
a1 b1
a2 b2
a3 b3
......
am-1 bm-1
am bm
其中 ai bi 表示能量从物种ai 流向物种bi
Input
第一行两个整数n 和 m。
接下来m行每行两个整数ai bi描述m条能量流动关系。
(数据保证输入数据符号生物学特点,且不会有重复的能量流动关系出现)
Output
一个整数即食物网中的食物链条数。
Sample Input
10 16
1 2
1 4
1 10
2 3
2 5
4 3
4 5
4 8
6 5
7 6
7 9
8 5
9 8
10 6
10 7
10 9
Sample Output
9
Hint
【样例解释】
就是上面题目描述1的那个图
各个物种的编号依次为
草 1兔 2狐 3鼠 4猫头鹰 5吃虫的鸟 6蜘蛛 7蛇 8青蛙 9食草昆虫 10
数据范围
1<=N<=100000 0<=m<=200000
题目保证答案不会爆int
题解
冠冕堂皇地出了一道$topsort$裸题...
我们为了方便统计答案将所有出度为$0$的点连向一个超级汇点。
然后按拓扑序进行$DP$,若边$u->v$将$ans[v] += ans[u]$。
另外特别注意单独的一个点不能组成食物链,所以对于入度和出度都是$0$的点我们不予考虑。
1 //It is made by Awson on 2017.10.1 2 #include <set> 3 #include <map> 4 #include <cmath> 5 #include <ctime> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <cstdio> 10 #include <string> 11 #include <cstring> 12 #include <cstdlib> 13 #include <iostream> 14 #include <algorithm> 15 #define LL long long 16 #define Max(a, b) ((a) > (b) ? (a) : (b)) 17 #define Min(a, b) ((a) < (b) ? (a) : (b)) 18 #define sqr(x) ((x)*(x)) 19 #define lowbit(x) ((x)&(-(x))) 20 using namespace std; 21 const int N = 100000; 22 const int M = 200000; 23 void read(int &x) { 24 char ch; bool flag = 0; 25 for (ch = getchar(); !isdigit(ch) && ((flag |= (ch == '-')) || 1); ch = getchar()); 26 for (x = 0; isdigit(ch); x = (x<<1)+(x<<3)+ch-48, ch = getchar()); 27 x *= 1-2*flag; 28 } 29 30 int n, m, u, v; 31 struct tt { 32 int to, next; 33 }edge[M+N+5]; 34 int path[N+5], top; 35 int in[N+5], out[N+5]; 36 int ans[N+5]; 37 38 void add(int u, int v) { 39 edge[++top].to = v; 40 edge[top].next = path[u]; 41 path[u] = top; 42 } 43 void topsort() { 44 queue<int>Q; 45 while (!Q.empty()) Q.pop(); 46 for (int i = 1; i <= n; i++) 47 if (!in[i]&&out[i]) { 48 Q.push(i); 49 ans[i] = 1; 50 } 51 while (!Q.empty()) { 52 int u = Q.front(); Q.pop(); 53 for (int i = path[u]; i; i = edge[i].next) { 54 int v = edge[i].to; 55 in[v]--, ans[v] += ans[u]; 56 if (!in[v]) Q.push(v); 57 } 58 } 59 } 60 void work() { 61 read(n), read(m); 62 for (int i = 1; i <= m; i++) { 63 read(u), read(v); 64 add(u, v); 65 in[v]++, out[u]--; 66 } 67 for (int i = 1; i <= n; i++) 68 if (!out[i]&&in[i]) add(i, n+1); 69 topsort(); 70 printf("%d ", ans[n+1]); 71 } 72 int main() { 73 work(); 74 return 0; 75 }