机器学习实战教程（一）：线性回归基础篇（中）

局部加权线性回归

---

　　线性回归的一个问题是有可能出现欠拟合现象，因为它求的是具有小均方误差的无偏估 计。显而易见，如果模型欠拟合将不能取得好的预测效果。所以有些方法允许在估计中引入一 些偏差，从而降低预测的均方误差。

　　其中的一个方法是局部加权线性回归（Locally Weighted Linear Regression，LWLR）。在该方法中，我们给待预测点附近的每个点赋予一定的权重。与kNN一样，这种算法每次预测均需要事先选取出对应的数据子集。该算法解除回归系数W的形式如下：

　　其中W是一个矩阵，这个公式跟我们上面推导的公式的区别就在于W，它用来给每个店赋予权重。

　　LWLR使用"核"（与支持向量机中的核类似）来对附近的点赋予更高的权重。核的类型可以自由选择，最常用的核就是高斯核，高斯核对应的权重如下：

　　这样就构建了一支只含对角元素的权重矩阵w，并且点x与x(i)越近， w(i, i)将会越大，k是我们唯一需要赋值的参数，他决定可权重的大小

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

font = FontProperties(fname=r"c:windowsfontssimsun.ttc", size=14)
def loadDataSet(fileName):
    """
    功能：导入数据
    输入：file
    输出：X， y
    """
    data = np.loadtxt(fileName)
    X = data[:,0:-1]
    y = data[:,-1]
    return X, y

def plotDataSet(fileName):
    """
    功能 画出原始的图像
    """
    xArr ,yArr = loadDataSet(fileName)
    
    m = len(xArr)
    xcode = []; ycode = []
    
    for i in range(m):
        xcode.append(xArr[i][1])
        ycode.append(yArr[i])
        
    yHat_1 = lwlrTest(xArr, xArr, yArr, 1.0)                            #根据局部加权线性回归计算yHat
    yHat_2 = lwlrTest(xArr, xArr, yArr, 0.01)                            #根据局部加权线性回归计算yHat
    yHat_3 = lwlrTest(xArr, xArr, yArr, 0.003)                            #根据局部加权线性回归计算yHat
    xMat = np.mat(xArr)                                                    #创建xMat矩阵
    yMat = np.mat(yArr)                                                    #创建yMat矩阵
    srtInd = xMat[:, 1].argsort(0)                                        #排序，返回索引值
    xSort = xMat[srtInd][:,0,:]
    fig, axs = plt.subplots(nrows=3, ncols=1,sharex=False, sharey=False, figsize=(10,8))                                        
    axs[0].plot(xSort[:, 1], yHat_1[srtInd], c = 'red')                        #绘制回归曲线
    axs[1].plot(xSort[:, 1], yHat_2[srtInd], c = 'red')                        #绘制回归曲线
    axs[2].plot(xSort[:, 1], yHat_3[srtInd], c = 'red')                        #绘制回归曲线
    axs[0].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5)                #绘制样本点
    axs[1].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5)                #绘制样本点
    axs[2].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5)                #绘制样本点
    #设置标题,x轴label,y轴label
    axs0_title_text = axs[0].set_title(u'局部加权回归曲线,k=1.0',FontProperties=font)
    axs1_title_text = axs[1].set_title(u'局部加权回归曲线,k=0.01',FontProperties=font)
    axs2_title_text = axs[2].set_title(u'局部加权回归曲线,k=0.003',FontProperties=font)
    plt.setp(axs0_title_text, size=8, weight='bold', color='red')  
    plt.setp(axs1_title_text, size=8, weight='bold', color='red')  
    plt.setp(axs2_title_text, size=8, weight='bold', color='red')  
    plt.xlabel('X')
    plt.show()
def lwlr(testPoint, xArr, yArr, k = 1.0):
    """
    函数说明:使用局部加权线性回归计算回归系数w
    Parameters:
        testPoint - 测试样本点
        xArr - x数据集
        yArr - y数据集
        k - 高斯核的k,自定义参数
    Returns:
        ws - 回归系数
    """
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
   
    weights = np.mat(np.eye(m))
    for j in range(m):
        diffMat = testPoint - xMat[j, :]
        weights[j, j] = np.exp(diffMat * diffMat.T / (-2.0 * k ** 2))
    xTx = xMat.T * (weights * xMat)                                        
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))                            #计算回归系数
    return testPoint * ws


def lwlrTest(testArr, xArr, yArr, k=1.0):  
    """
    函数说明:局部加权线性回归测试
    Parameters:
        testArr - 测试数据集
        xArr - x数据集
        yArr - y数据集
        k - 高斯核的k,自定义参数
    Returns:
        ws - 回归系数
    """
    m = np.shape(testArr)[0]                                            #计算测试数据集大小
    
    yHat = np.zeros(m)    
    for i in range(m):                                                    #对每个样本点进行预测
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat
        


    
if __name__ == "__main__":
    plotDataSet("data.txt")
   

---

 

---

岭回归为什么会被提出来？ 

1. 岭回归最初的提出是为了解决特征数多于样本数的情况
2. 现在也用于在估计中加入偏差，从而得到最好的估计

如何实现了解决过拟合问题的？

　　首先是 入 ，这个值小，表示惩罚项所占的份额比较小，若值大，表示惩罚项所占的份额比较大

　　其次。我们可以通过通过选择多次 入 值，比较，判断哪个值的效果更好。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
import numpy as np
import matplotlib.pyplot as plt

boston = load_boston()
X = boston.data
y = boston.target

# 1 将数据进行切分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)

n_alphas = 200
alphas = np.logspace(-1, 5, n_alphas)

coefs = []
for a in alphas:
    ridge = Ridge(alpha=a, fit_intercept=False)
    ridge.fit(X_train, y_train)
    coefs.append(ridge.coef_)

ax = plt.gca()

ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()

 

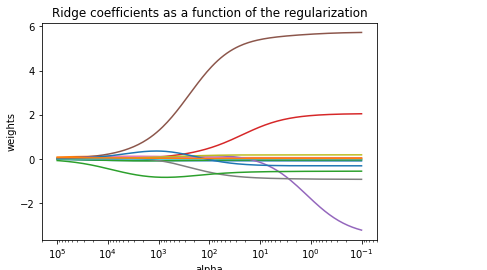
　　根据得到的图，我们可以找到合适的 入 值

　　另外，我们也可以根据这个图，选择比较合适的特征，图中，岭回归其实就是L2 范数，可以解决 ill condition 问题