题目描述
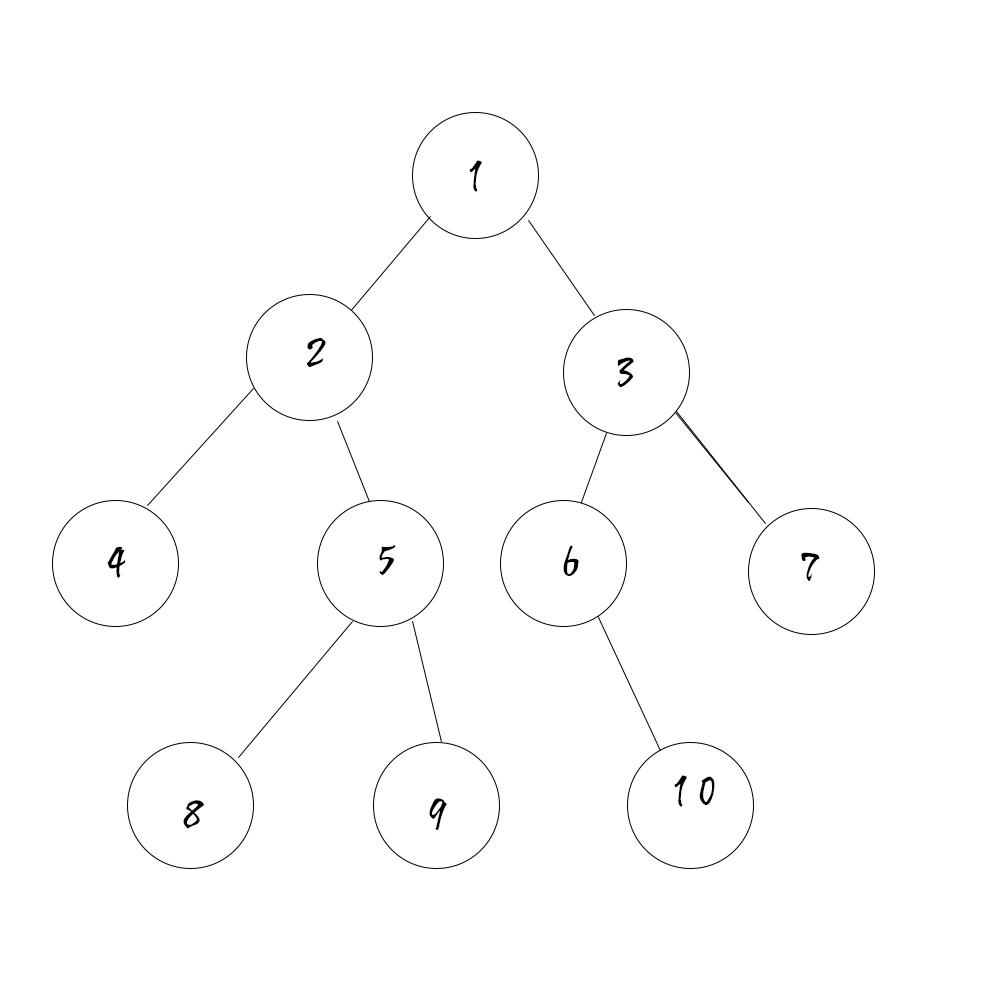
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为:
深度:4 宽度:4(同一层最多结点个数)
结点间距离: ⑧→⑥为8 (3×2+2=8)
⑥→⑦为3 (1×2+1=3)
注:结点间距离的定义:由结点向根方向(上行方向)时的边数×2,
与由根向叶结点方向(下行方向)时的边数之和。
输入格式
输入文件第一行为一个整数n(1≤n≤100),表示二叉树结点个数。接下来的n-1行,表示从结点x到结点y(约定根结点为1),最后一行两个整数u、v,表示求从结点u到结点v的距离。
输出格式
三个数,每个数占一行,依次表示给定二叉树的深度、宽度及结点u到结点v间距离。
这道题有明显的板子气息。如果只看节点间距离的话,明显是求两个点的LCA,即最近公共祖先。
最近公共祖先(Lowest Common Ancestors),是指对于有根树T的两个结点u、v,LCA(T,u,v)表示一个结点x,满足x是u和v的祖先且x的深度尽可能大。特别的,一个点也是它自身的祖先。(想了解更多戳这里)
我们以上图为例:

以4和8的最近公共祖先为例,我们可以发现,4的祖先是4、2、1, 8的祖先是8、5、2、1, 相同的祖先是2和1,而2号节点深度为2,1号节点深度为1,所以2是4和8的最近公共祖先。
再以3和10为例,3的祖先是3、1, 10的祖先是10、6、3、1,按照定义,这两点的LCA是3。
通过以上两个例子我们就能得到几个基础结论:
1、对于任意一颗有根树T,任意两点都存在LCA,因为它们至少有根节点这一个相同的祖先。
2、若A是B的祖先,则LCA(A, B) == A。
我们也可以据此再给最近公共祖先下一个比较严谨定义:对于一颗有根树T,设节点u的祖先组成集合A,节点v的祖先组成集合B,则LCA (u,v) 等于A∩B中深度最大的点。
理论储备好了,就到了写程序的时候。
LCA该如何求呢?我们稍加思考便能知道,既然LCA是两个节点的公共的祖先,那让这两个节点一起往上跳,碰面的点不就是它们的LCA了吗?这思路乍一看没有问题,但却忽略了一个重要的因素:如果这两个节点在同一层,那让它们一起跳确实可以找到LCA,但若它们的深度不同,比如上图中的4和8,稍加模拟就会发现,它们是无法碰面的,准确来说,是不会在路上碰面,而会在根节点1出碰面,按照我们的算法,LCA(4, 8)就是1,然而我们在上文已经推演过,LCA(4, 8)是2。这说明我们的思路有问题。或许有人在这一步就会推翻之前的猜想,从头再来。其实不然,一起向上挑是没问题的,我们只要事先做一个预处理,让两个点先处于同一深度,就能解决这个问题了。代码在下文一起呈现。
既然用到了深度,那我们势必要先遍历一遍树求出每个点的深度,方法较多,这里不再展开讲。
于是我们便能写出求LCA的代码了:
int lca (int x, int y) //求最近公共祖先 { if (dep[x] < dep[y]) swap (x, y); //确保被操作的点的深度更大 while (dep[x] > dep[y]) //让深度大的点向上跳,直到两个点深度一样 { x = fa[x]; } if (x == y) return x; //如果一个点是另一个点的祖先,返回这个点 while (x != y) //一起向上跳 { x = fa[x]; y = fa[y]; } return x; //返回LCA }
这算法很容易理解,貌似是个好算法,但!是!我们不要忘了TLE这种错误(别问我怎么记住的),我们可以想一下,这种算法是一步一步向上跳,每一层都要走一遍,效率并不高,特别是让两个点到同一深度的步骤,我们明明知道它们分别的位置,却让更深点一步一步跳,浪费了时间。为了解决这个问题,我们要用到另一种算法——倍增。
所谓倍增,就是按2的倍数增大,即1,2,4,8,16……利用我们小学二年级就学过的知识,我们可以轻易推出,2的倍数可以组成任何正整数,所以用倍增不用担心跳不到。需要注意的是,在这里我们要从大往小跳,即跳……16,8,4,2,1,至于为什么这么做,我们煮一个栗子,跳5,如果从小到大跳,那么就是1->2->4,这时我们发现超过了5,就要回溯, 变成1->4,这显然浪费时间,但如果从大到小,就可以直接4->1,节省了时间。利用倍增,时间复杂度降为O(nlogn)。
void dfs (int now, int fatherx) ////now表示当前节点,fatherx表示它的父亲节点 { fa[now][0] = fatherx; dep[now] = dep[fatherx] + 1; for (r_r int i = 1; i <= lg[dep[now]]; i++) { fa[now][i] = fa[fa[now][i - 1]][i - 1]; //这里利用了小学二年级就学过的数学知识:2^i = 2^(i-1) + 2^(i-1) //意思是now的2^i祖先等于now的2^(i-1)祖先的2^(i-1)祖先 } for (r_r int i = head[now]; i; i = edges[i].nxt) { if (edges[i].to != fatherx) dfs (edges[i].to, now); } }
--------------------------------------------------------------------------
接着是对算法进行一个常数优化,lg数组在这里发挥作用了
for (r_r int i = 1; i <= n; i++) //预先算出log_2(i)+1的值,用的时候直接调用就可以了 { lg[i] = lg[i - 1] + (1 << lg[i - 1] == i); //这里的(1 << lg[i - 1] == i)类似于bool,若等号成立返回数值1,否则返回数值0 }
这里刚看可能会懵掉,手动推一下能帮助理解。
--------------------------------------------------------------------------
然后就是最重要的求LCA,这里的lg就起到了优化作用。
int lca (int x, int y) { if (dep[x] < dep[y]) swapxs (x, y); while (dep[x] > dep[y]) { x = fa[x][lg[dep[x] - dep[y]] - 1]; } if (x == y) return x; for (r_r int k = lg[dep[x]] - 1; k >= 0; k--) { if (fa[x][k] != fa[y][k]) { x = fa[x][k]; y = fa[y][k]; } } return fa[x][0]; }
有了这些,我们就能轻易求出两个点的LCA了。回到题目,深度可以再遍历时顺便求出,宽度可以单独求出,有了LCA, 距离也很容易求得。
完整代码如下:
#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <queue> #include <vector> #define r_r register #define ll long long using namespace std; const int maxn = 100010; inline int read() { int s = 0, f = 1; char ch = getchar(); while (ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar();} while (ch >= '0' && ch <= '9') {s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar();} return s * f; } int maxxs (int x, int y) {return x > y ? x : y;} //自定义些基础函数 int minxs (int x, int y) {return x < y ? x : y;} void swapxs (int &x, int &y) {x ^= y ^= x ^= y;} int n, tot, lcaxs, disx, max_dep = -1, max_wid = -1; int head[maxn], dep[maxn], lg[maxn], wid[maxn], fa[maxn][22]; struct node //普通的存图 { int nxt, to; } edges[maxn << 1]; void addx (int x, int y) { edges[++tot].to = y; edges[tot].nxt = head[x]; head[x] = tot; } void make_tree() { n = read(); for (r_r int i = 1; i <= n - 1; i++) { int x = read(), y = read(); addx (x, x); addx (y, y); } for (r_r int i = 1; i <= n; i++) //预处理 { lg[i] = lg[i - 1] + (1 << lg[i - 1] == i); } } void dfs (int now, int fatherx) { fa[now][0] = fatherx; dep[now] = dep[fatherx] + 1; for (r_r int i = 1; i <= lg[dep[now]]; i++) { fa[now][i] = fa[fa[now][i - 1]][i - 1]; } for (r_r int i = head[now]; i; i = edges[i].nxt) { if (edges[i].to != fatherx) dfs (edges[i].to, now); } max_dep = maxxs (max_dep, dep[now]); //求出深度 } int lca (int x, int y) { if (dep[x] < dep[y]) swapxs (x, y); while (dep[x] > dep[y]) { x = fa[x][lg[dep[x] - dep[y]] - 1]; } if (x == y) return x; for (r_r int k = lg[dep[x] - 1]; k >= 0; k--) { if (fa[x][k] != fa[y][k]) { x = fa[x][k]; y = fa[y][k]; } } return fa[x][0]; } int find_max_wid() //找出宽度 { for (int i = 1; i <= n; i++) { wid[dep[i]]++; } for (int i = 1; i <= max_dep; i++) { max_wid = maxxs (max_wid, wid[i]); } return max_wid; } int find_disx() //根据题意求距离 { int x = read(), y = read(); lcaxs = lca (x, y); disx = (dep[x] - dep[lcaxs]) * 2 + dep[y] - dep[lcaxs]; //题目中公式的应用 return disx; } int main() { make_tree(); dfs (1, 0); printf ("%d %d %d ", max_dep, find_max_wid(), find_disx()); return 0; }
代码已做防复制处理,核心代码没有问题,只再一个你不会发现的地方做了改动。