先手一个题目链接。
题意
现在聚会上有n个人参加,然后依次按照规律离开,第一次是有0个朋友的人离开,第二次是有1个朋友的人离开,第三次是有2个朋友的人离开,之后依次是有3,4,5,6……n-1个朋友的依次离开,求最后聚会最多将会剩下多少人。
输入:第一行一个整数t,表示数据组数,之后t行每行一个整数n。
输出:对于每组数据,输出一个答案。
1<=t<=100000 , 1<=n<=100000。
输入输出样例
当n == 0 :
Party貌似并没有举行,或者,是压根就没人来,故最终只能剩下0人。
当n == 1:

此时只有A一个人来了,那么A当然不会有在场的朋友,于是,A在第一轮就立凯了(好惨一A),最终剩下0人。
当n == 2:
第一种情况,A和B虽然都来了,但是他们并不是好盆友,所以都会在第一轮立凯,最终剩下0人。
第二种情况,A和B是好盆友,他们手牵着手♂来到了Party,并成功活过了第一轮。但是,第二轮中刷掉有一个朋友的,A和B都有一个朋友,所以还是得立凯。故最终剩下0人。
综上,n == 2时最多剩下0人。
到这里我不禁想,办Party的人有毛病吧,当人数<= 2,就一个留下的都没有。
但是不慌,或许人家就是想人不多就不开呢?我们继续推导下去。
当n == 3:
第一种情况,A、B、C三人互不认识,在第一轮全部立凯。
第二种情况,三人中有且只有两人认识,第一轮中落单的C像飘零的孤鸟一般默默离去,第二轮中A和B携手立凯,最终剩下0人。
第三种情况,三人中有一个人同时和另外两人有关系♂,则第一轮无人立凯,第二轮B和C因为都有A这个“好兄弟♂”,只能立凯,此时只剩A一个人,而第三轮立凯的条件是有2个朋友,A此时没有朋友,不会立凯,同理,之后的轮次中A也会活下来,直到Party结束。故最终剩下一个人。
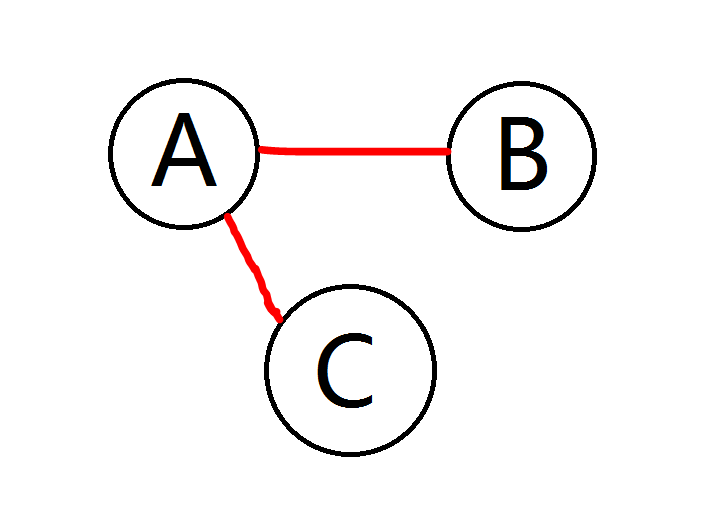
第四种情况,A、B、C都互相认识,三人都会在第三轮立凯,最终剩下0人。
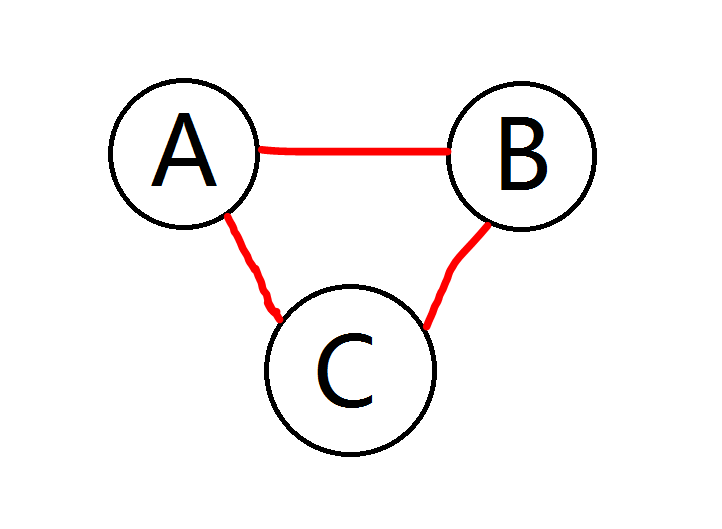
综上,当n == 3,最多剩下一人。
到这里事情有了转机,最多剩下的终于不是0人。这使我们有了一丝希望。
当n == 4:
第一种情况,4人互不认识,第一轮全部立凯。

第二种情况,4人中有且只有两人认识,第一轮落单的C和D立凯,第二轮A和B立凯,最终剩下0人。
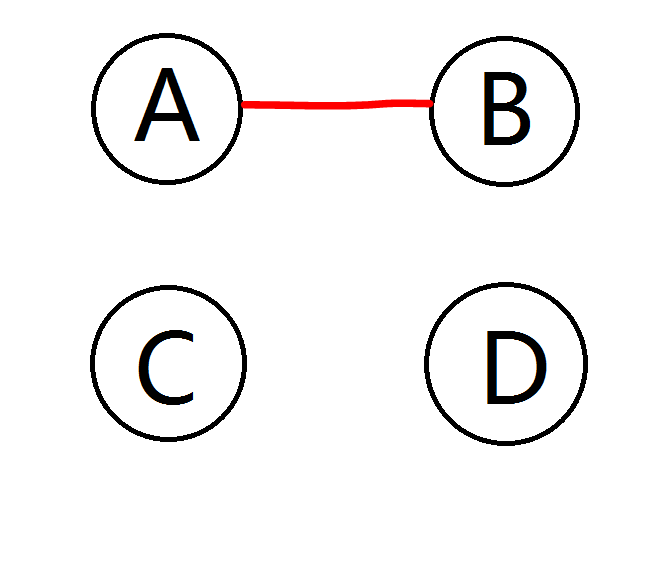
第三种情况,如图(由于Na2S2O3语文太差已经不想用语言叙述),第一轮D立凯,第二轮B与C立凯,A活到最后,最终剩下一人。
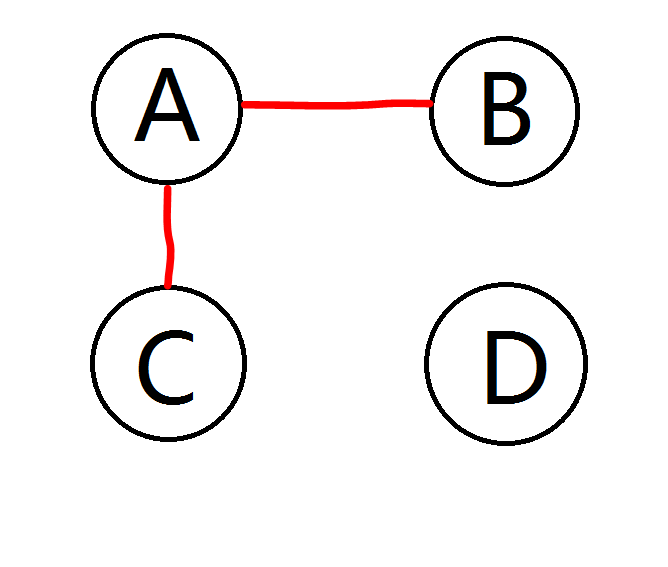
第四种情况, 如图,第一轮无人立凯,第二轮B、D立凯,此时A和C都只剩一个朋友,不满足之后立凯的条件,故最终剩下2人。
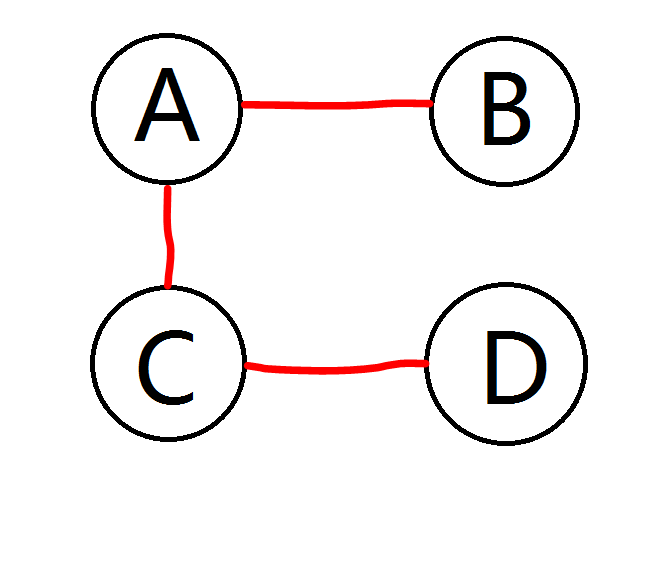
情况当然还有很多,这里不再枚举,读者感兴趣可以自己画一下。最终我们发现,当n == 4,最多剩下2人。
这时似乎就有些规律了,当n>2时,最多剩下的人数是n-2。
这个式子看上去有些玄学,我们在这里简单推导一下。
不妨设共有n人,每个人都互相认识,即每个人都有n-1个朋友,则所有人都会在n轮立凯。我们切断第一个人与第n个人的联系,不让他们当朋友,则已知第1轮到第n-2轮都没人立凯,而在第n-1轮,有n-2个朋友的人要立凯,于是第一个人和第n个人就立凯了,此时剩下的人还有n-2个朋友,不会在第n轮立凯,故最多剩下n-2人。若每个人并非都互相认识,则必然有人会提前立凯,使最终剩下的人数减少。故最多剩下的人数为n-2。
以上内容只是我个人的理解,若有错误还望读者指出。
附AC代码:
#include <cstdio> using namespace std; int t, n; int main() { scanf ("%d", &t); while (t--) { scanf ("%d", &n); printf ("%d ", n > 2 ? n - 2 : 0); //三目运算,意为:若n>2,输出n-2,反之输出0 } return 0; }
由此看来,这道题的难度绝不是绿题,只要认真想很容易解决。标签并不见得十分准确,所以以后做题不要被吓到,认真思考,总会有收获。
既然这题标签已经这么不准了,我们不如联系管理员把它改成黑的吧。