所谓孪生素数,就是相差为2的素数对,例如3和5,11和13。如果仅仅是100以内的孪生素数,相信大部分人只用数就能数出来,毕竟100以内只有25个素数。但是如果是1000以内呢?100000以内呢?如果像题目中说的一样,一亿以内呢?
硬着头皮数显然不行了,要解决这个问题,我们要依赖于编程。
要求孪生素数的对数,首先要找到孪生素数,要找到孪生素数,首先要找到素数。C++中有许多找素数的方法,比如基础的试除法,其代码如下:
bool prime(int n) { if(n<2) return false; for(int i=2;i*i<=n;i++) { if(n%i==0) return false; } return true; }
这段代码比较基础,也很容易理解。
完整程序如下:
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int n,cnt; //cnt记录孪生素数对数 bool prime(int n) //试除法筛素数 { if(n<2) return false; for(int i=2;i*i<=n;i++) { if(n%i==0) return false; } return true; } int main() { scanf("%d",&n); for(int i=2;i<=n;i++) { if(prime(i)&&prime(i+2)) //判断是否满足孪生素数定义 { cnt++; } } printf("%d ",cnt);return 0; }
一切都很顺利的进行了,我们不禁暗想:
孪生素数,就这???
然而,当输入“100000000”时,奇怪的事情发生了,答案久久没有出现在小黑板上,只有光标在闪动着寂寞的白光,宛若孤独而无人陪伴的我。
这令人疑惑,于是我关闭了窗口,重新运行,并输入了较小的数。答案几乎是在敲回车后的一刹那出现在小黑板上。
这说明程序没有问题,输入“100000000”答案迟迟不出现,只有一个可能——程序在运算结果。
既然如此,那我们能做的就只有等待。
终于,在不知多久之后,小黑板上终于出现了我们所希望看到的东西——440312。
虽然得到了结果,但比起这个,我们更想知道它到底算了多久,于是我在程序中加入了从百度抄来的计时程序,如下:
#include<iostream> #include<cstdio> #include<algorithm> #include<time.h> //头文件 using namespace std; clock_t start,finish; //定义始终 double duration; //定义时间 int n,cnt; bool prime(int n) { if(n<2) return false; for(int i=2;i*i<=n;i++) { if(n%i==0) return false; } return true; } int main() { scanf("%d",&n); start=clock(); //在程序开始运行时开始计时,注意,若将这句话加在输入之前,会把输入数据的时间记入,影响结果 for(int i=2;i<=n-2;i++) { if(prime(i)&&prime(i+2)) { cnt++; } } finish=clock(); //结束计时 duration=(double)(finish - start)/CLOCKS_PER_SEC; //计算时间 printf( "%f seconds ",duration); //输出时间 printf("%d ",cnt);return 0; }
当输入“10000”,运算时间为0.002000s,输入“1000000”,运算时间为0.310000s,两次运算时间并没有差很多。
但输入“100000000”,在又一次漫长的等待后,小黑板上出现了惊人的149.797000s,是计算1000000以内的孪生素数对数所用时间的约483倍。
这可怕的数字令我们感到恐惧,若是数据范围再大一些,试除法岂不是要算一年!
看来数据太大,用试除法求解是行不通了,我们需要的是效率更高的算法。
提到高效算法,聪明的你一定能想到Eratosthenes筛选法,翻译成人话就是埃氏筛。
埃氏筛的基本思想:素数的倍数一定不是素数。先假设所有数都是素数,从小到大枚举每一个素数x,把x的倍数都标记为非素数。当从小到大扫描到一个数x时,若它尚未被标记,则它不能被2~x-1之间的任何数整除,该数就是素数。(对整数1特殊处理)
埃氏筛代码如下:
void primes(int n) { memset(v,0,sizeof(v)); //合数标记 for(int i=2;i<=n;i++) { if(v[i]) continue; cout<<i<<endl; //i是素数 for(int j=i;j<=n/i;j++) { v[i*j]=1; } }
}
埃氏筛的时间复杂度是O(nloglogn),效率非常接近线性,是一种常用的素数筛法。然而,埃氏筛会对合数进行重复标记,即使是优化之后,其根本原因是算法不能唯一确定产生合数的方式。据此,我们在生成一个需要标记的合数时,每次只向现有的数乘上一个质因子,并且让它是这个合数的最小质因子。这相当于让合数的质因子从大到小累积。具体来说,我们采用如下的筛法:
int v[maxn],prime[maxn]; void primes (int n) //用线性筛找素数 { memset(v,0,sizeof(v)); //最小质因子 m=0; //素数数量 for(int i=2;i<=n;i++) { if(!v[i]) //i是质数 { v[i]=i; prime[++m]=i; } //给当前的数i乘上一个质因子 for(int j=1;j<=m;j++) { //i有比prime[j]更小的质因子,或者超出n的范围 if(prime[j]>v[i]||prime[j]>n/i) break; //prime[j]是合数i*prime[j]的最小质因子 v[i*prime[j]]=prime[j]; } } }
这便是线性筛。每个合数只会被它的最小质因子筛一次,时间复杂度为O(N)。
筛法介绍完了,求孪生素数对的程序也就不难写了,只需要判断与一个素数相差2的数是否为素数即可。这个任务交给读者自行完成。
下面我简要说一下测评结果。
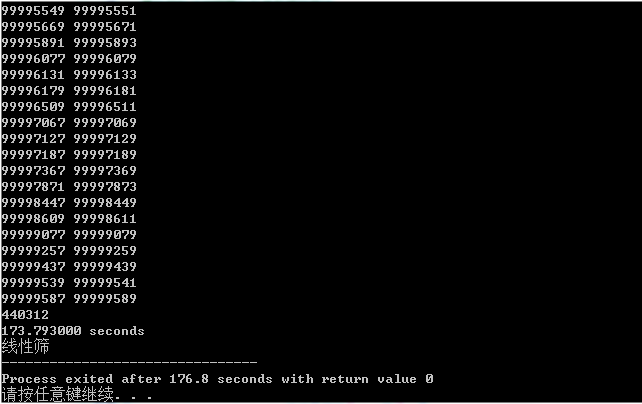
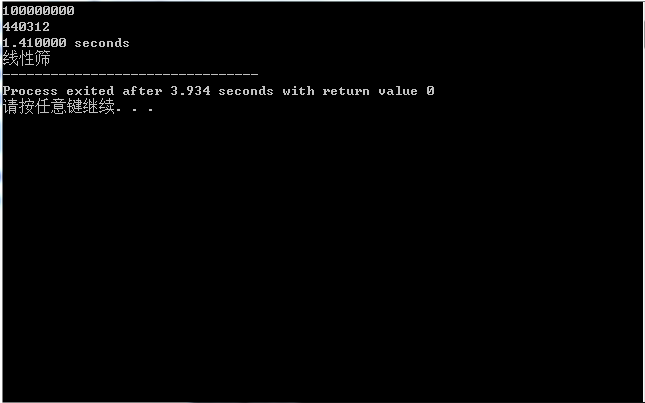
这是使用线性筛求对数并输出孪生素数对的运行结果,总共跑了173.793000s,若仅仅输出对数,只需要1.410000s,比试除法快了近107倍。
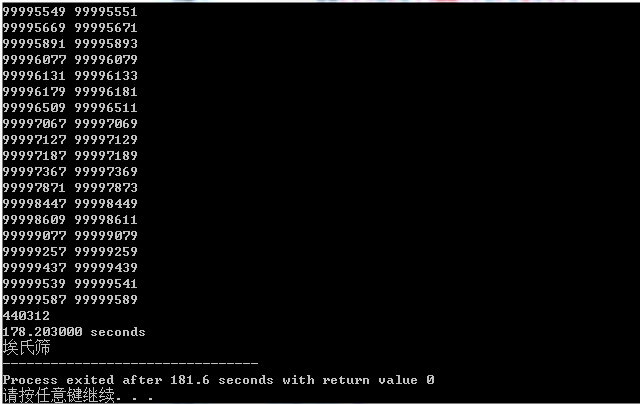
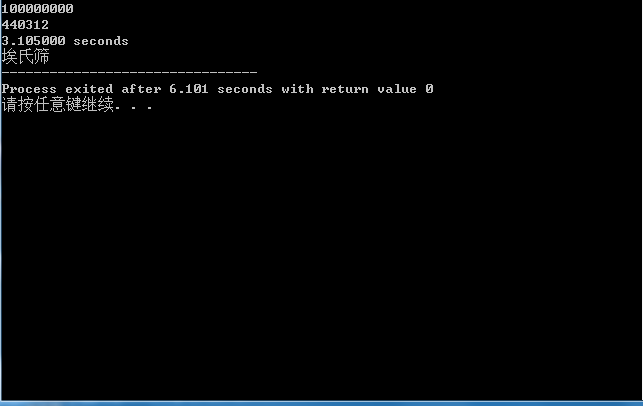
埃氏筛也不敢示弱,跑出了178.203000s和3.105000s的不俗成绩。
(顺便一提,用试除法求孪生素数对,如果要输出孪生素数是什么,它需要跑约328s)
相比于基础的试除法,这两种算法的效率都高得没话说。
正所谓,永恒与刹那间,只隔着我的算法。既然有算法能几秒内解决问题,那为什么不用呢?多节约出几分钟,不就能多听几首银临的歌了吗。
所以,下次有个要求素数的题,尝试用埃氏筛和线性筛吧。
如果这篇博客对你有帮助,就请留下一个大拇指,最好还能点个推荐,求求您了,俺求求您了!