题目描述：
平面上有 n 个没有公共点 的圆。你要从点(x1,y1)走到(x2,y2)。问你最少要经过多少圆的边界。保证这两个点都不在圆的边界上。
输入格式：
问题输入： 第一行一个整数 n， 1<=n<=50。 接下来三行每行 n 个整数，分别表示 n 个圆的圆心和半径，格式如下： x1,x2……xi……xn ， y1,y2……yi……yn ， r1,r2……ri……rn -1000<=xi,yi<=1000,1<=ri<=1000 。最后一行四个整数 x1,y1,x2,y2， -1000<=x1,y1,x2,y2<=1000。
输出格式：
问题输出： 一个整数，意义如上。
样例：
输入： 输入：
3 1
0 -6 6 0
0 1 6 0
2 2 2 2
-5 1 5 1 -5 1 5 1
输出：
1 0
luogu链接：https://www.luogu.com.cn/problem/T139630
相信大家看到这道题的第一印象都是：
好 ~~一 ~~道 ~~水~~题 ~~
循环输入这些玩意，把起点终点一连，写个计数器，搞几个判断不就完了吗，这题不是有手就行？？？
然而，事实真的如此吗？
根据题意，我们很容易画出样例图：
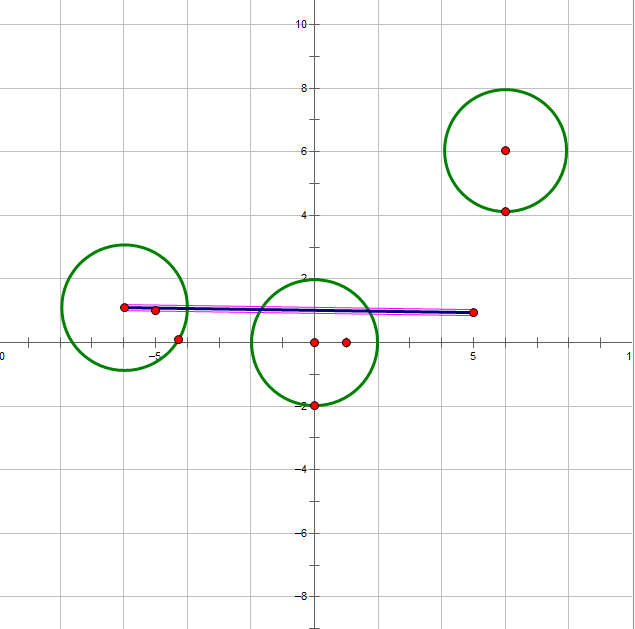（样例一）（请原谅我拙劣的画图技术）
WTF？！？！？！？！
这明明经过了2个圆的边界，为啥子样例输出是1？？？
难道样例有问题？？？
样例二也有相同的问题，在图上穿过了一个一个圆，而输出却是0。
经验告诉我们样例错误的情况极少出现，更何况一次错两个。出问题的一定是我们自己。
我们不妨重新审视一下题目。
注意【你要从点(x1,y1)走到(x2,y2)】，题目中仅仅说走到，却丝毫未提及怎么走。难道道路只有连接两点的一条吗？显然并非如此。题目中没有说必须走直线，翻译过来就是：只要能到，你怎么蛇皮走位都没问题。
于是，样例一便可以这么走：
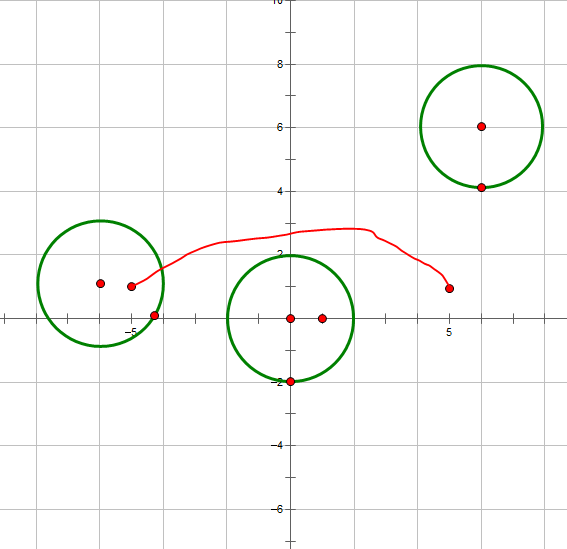
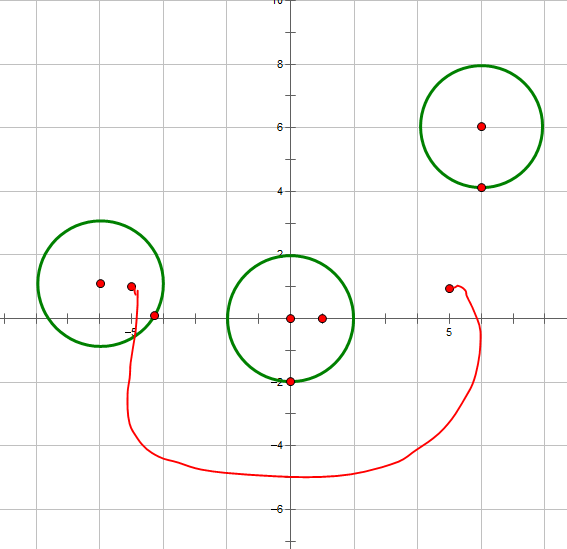
甚至这样走：
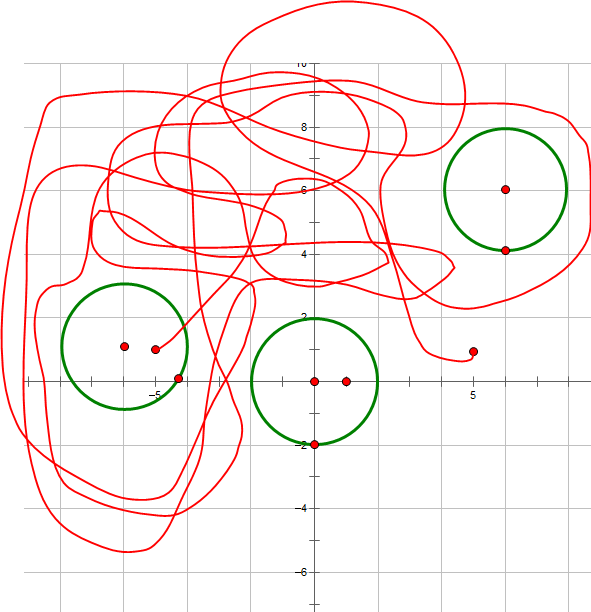
这样都满足了从一点到另一点的要求，而且只穿过一个圆，符合样例输出。
结合上图可知，与穿过几个圆直接挂钩的是起点和终点是否在圆内，若在，则会穿过一圆。
而点是否在圆内，只需要比较点到圆心的距离与该圆半径，若距离>半径，则点在圆外，若距离<半径，则点在圆内（数据保证点不在圆上）。
故我们可以写出程序：
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int n,x[60],y[60],r[60]; int s1,s2,s3,x01,y01,x02,y02; int main() { scanf("%d",&n); int count=0; for(int i=1;i<=n;i++) //注意输入圆心和半径要分开输入 { scanf("%d",&x[i]); } for(int i=1;i<=n;i++) { scanf("%d",&y[i]); } for(int i=1;i<=n;i++) { scanf("%d",&r[i]); } scanf("%d%d%d%d",&x01,&y01,&x02,&y02); for(int i=1;i<=n;i++) { s1=sqrt((x01-x[i])*(x01-x[i])+(y01-y[i])*(y01-y[i])); //计算点到圆心距离 s2=sqrt((x02-x[i])*(x02-x[i])+(y02-y[i])*(y02-y[i])); if(s1<r[i]) count++; //判断点到圆心距离和半径哪个大 if(s2<r[i]) count++; } printf("%d",count); return 0; }
这段程序看上去没什么问题，两个样例也都能过，那就交吧！
然而…………
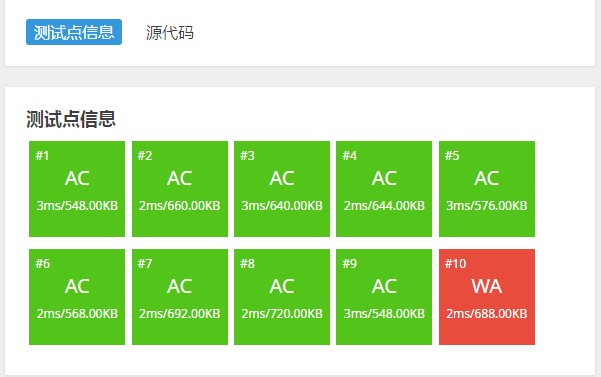
WA~~~~~~~~~~~~~~~~~~~~
最后一个测试点没有过，说明还有问题。
遇到只错了一个测试点的情况，我们该怎么办呢？
当然是卡测试点继续debug。
我们上上方的程序中判断计数是否加一，是通过比较点到圆心距离和圆的半径，但是这种操作并不适用于一种较特殊的情况，如图：
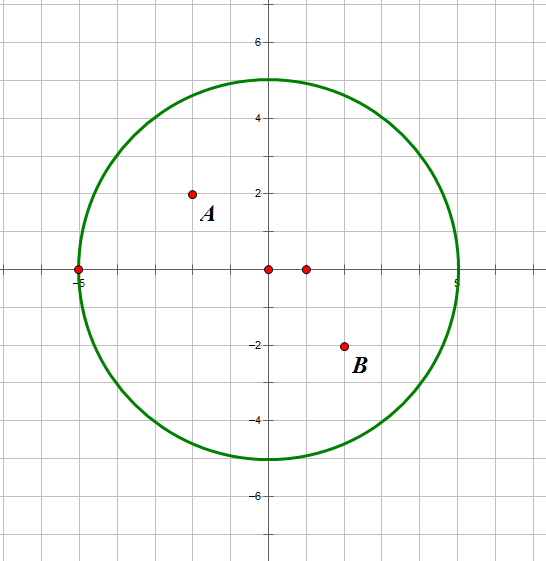
很明显，这种情况下从A到B需要穿过的圆的数目为0，但若以我们的评测标准，因为A和B到圆心距离都小于圆的半径，计数会加2，所以得出的答案是2，明显错误。这就是两点在同一圆内的特殊情况，需要另加判断。
我们很容易发现，在这种情况下，两个点到圆心的距离都小于半径，而之前的情况是一个点到圆心距离小于半径、一个大于半径，于是，我们便可以由此写出特判程序：
if(s1<r[i]&&s2<r[i]) continue; //使用continue直接跳过此情况。注意，要先判断是否在同一圆内，否则计数会先加2 else if(s1<r[i]||s2<r[i]) count++;
到此这道题就全部结束了，AC代码：
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int n,x[60],y[60],r[60]; int s1,s2,s3,x01,y01,x02,y02; int main() { scanf("%d",&n); int count=0; for(int i=1;i<=n;i++) { scanf("%d",&x[i]); } for(int i=1;i<=n;i++) { scanf("%d",&y[i]); } for(int i=1;i<=n;i++) { scanf("%d",&r[i]); } scanf("%d%d%d%d",&x01,&y01,&x02,&y02); for(int i=1;i<=n;i++) { s1=sqrt((x01-x[i])*(x01-x[i])+(y01-y[i])*(y01-y[i])); s2=sqrt((x02-x[i])*(x02-x[i])+(y02-y[i])*(y02-y[i])); if(s1<r[i]&&s2<r[i]) continue; else if(s1<r[i]||s2<r[i]) count++; } printf("%d",count); return 0; }
小蒟蒻的此篇题解就到此结束了，喜欢的话还请留下一个大拇指。