Softmax 用于在深度学习中处理多分类(C > 2)问题,分类器最后的输出单元需要Softmax 函数进行数值处理。关于Softmax 函数的定义如下所示:
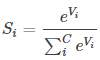
其中vi表示 vi = z[L] = w[L]a[L-1]+b[L]
t = e[Vi]
举个例子:
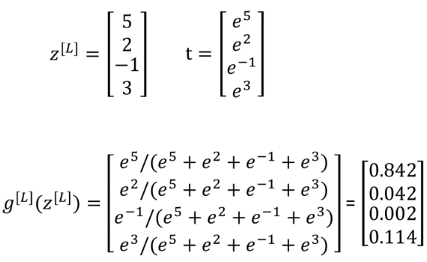
这样就对应着最终分类的四个类别的概率
与softmax对应的就是hardmax
对应上面的例子就是形成一个[1,0,0,0]T的结果,即在最大的元素位置填1,其他的都填0
另外如果将softmax局限在C=2的条件下,事实上就变成了了一个logistic regression
softmax损失函数:
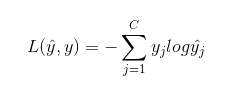
假设原类别y=[0,1,0,0] y^=[0.3,0.2,0.1,0.4]
那么从损失函数来看把yj为0的项全舍去,只剩下-y2logy^2=-logy^2=-log0.2=0.70
也就是说损失函数利用了最大似然估计,放大计算了真实类别下的差距