参数重要性:
第一阶:α即learning rate
第二阶:momentum中的β,hidden units的数量,mini-batch的大小
第三阶:hidden layers的数量,learning rate decay的参数
参数选择的方式:
一、完全在一定范围内进行随机
二、尝试完毕上述随机参数后,以粗糙到精确的思路,缩小随机范围并重复第一步
python中参数的具体实现:
对于学习率α而言:0 < α < 1
所以打个比方如果测试 0.0001 ≤ α ≤ 1显然这是一种指数分布,如果直接随机数那么90%的可能性都会取到[0.1,1]之间,只有10%的资源会去测试[0.001,0.1]这显然是不合理的,所以使用以下方法
r = -4 * np.random.rand() 此时会随机出一系列[-4,0]区间的数
α = 10r即可
对于动量梯度下降法momentu中的β而言:假设 0.9 < β < 0.999
我们知道1/1-β就是β平均的范围,比如取0.9的时候它就平均了10天内的温度,取0.999它就平均了1000天内的温度
所以实质上我们是在取1-β在[0.1,0.001]上的取值
因此r的范围就是[-1,-3]
1-β = 10r
β = 1-10r
迭代模型的过程:感谢吴恩达老师的公开课,以下图片均来自吴恩达老师的课件
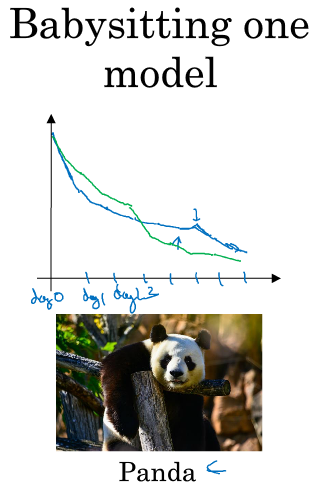
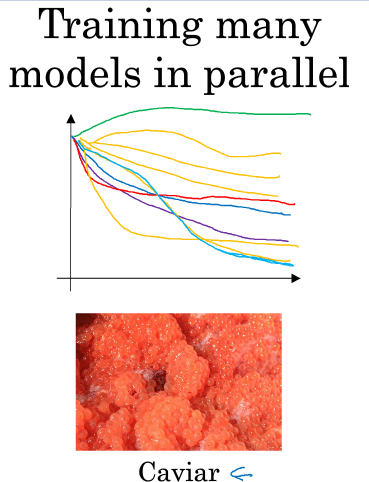
前者是一次训练一个模型,并每天在这个模型的基础上进行优化直到这个模型收敛到一定精度,适用于计算资源有限且数据量较大的环境
后者是一次训练多个模型,在多个模型中直接找到较为优秀的模型然后再进行优化,适用于有海量算力的环境