原题链接:https://www.luogu.org/problem/P2015
题意就是给你n-1条树枝,每条树枝上都带有一定的苹果,问最后留下m根树枝,能拥有的苹果的最大值,根节点为1,每个节点只有2种情况,有2个儿子,或没有儿子。
这题是一个很典型的树形结构,因为节点以边相连,又为二叉结构,无环。我们这时候从根节点下顺,找到最深的儿子,然后一步步开始回溯,以当前回溯到的这个点作为根,考虑他
有几条边的最大值。那从下至上递推回去,根节点的状态只与2个子节点有关,很明显,这就是一个dp,且是树形的。
本题的状态转移方程要先列出:dp[i][j]=max{ dp[i][j],dp[i][j-k-1]+dp[son[i]][k]+val[i][son[i]] }(0<=j<=m,0<=k<j).接下来解释这个方程从何而来。
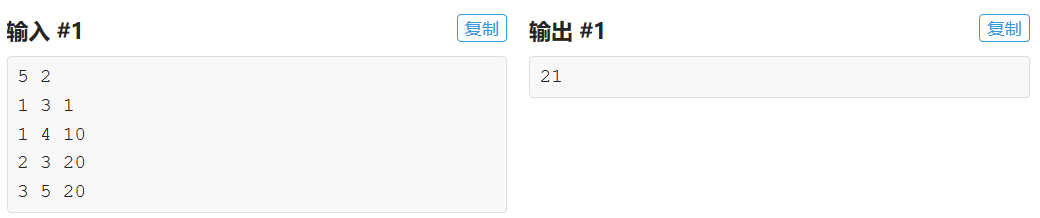

以样例为例,我们这时候从根节点1向下搜索,找到了2,可是2这时候作为单点,并不存在边,便回溯,到3,这时候3-2有一条边,我们可以考虑是否要添这条边,dp[3][1]这时候要由dp[2][0]
转移而来,为什么呢,因为这时候3如果要与2相连,是肯定要加3-2这条边,不然子树与根就无法连接起来了吧。接下来查到5这个点回溯,可以处理dp[3][2]了,dp[3][2]只由dp[5][0]和dp[5][1]而来,
因为3-2处理过了对吧,由dp[5][1]而来的时候,为什么加的是dp[3][0]呢?(请注意观察式子,可以用笔推导),因为前面有提到过,若要根与子树相连,必须选取根与子树的根的边。所以整个式子
就很好理解,你当前的这个点的儿子取j条边,你的根就只能取m-j-1条边。
代码实现如下:
#include<iostream> #include<vector> #include<cstring> using namespace std; int dp[105][105]; vector<int>son[105]; int val[105][105]; int vis[105]; int n,m; void dfs(int x) { int len=son[x].size(); vis[x]=1;///经过的点打上标记,不再处理 for(int i=0;i<len;i++) { int y=son[x][i]; if(vis[y]==1) { continue; } vis[y]=1;///谁先到谁是爹 dfs(y); for(int j=m;j>=1;j--) { for(int k=j-1;k>=0;k--) { dp[x][j]=max(dp[x][j],val[x][y]+dp[y][k]+dp[x][j-k-1]);///文中解释 } } } } int main() { cin>>n>>m; memset(vis,0,sizeof(vis)); for(int i=1;i<n;i++) { int u,v,w; cin>>u>>v>>w; son[u].push_back(v); son[v].push_back(u); ///这里建双向边,主要是不知道哪个是父亲,所以添加双向边。 val[u][v]=w; val[v][u]=w; ///这里我与网上的做法不同,他们喜欢把值赋予节点上,那样子不好理解,这样的赋值可以直观看出他就是边权 } dfs(1);///从根节点开始 cout<<dp[1][m]<<endl;///回溯至最开始的根节点,m条边的最大值 }