题面
在一个偶然的情况下,你获得了一台3D打印机。
你因此获得了一项殊荣,那就是为玩具公司设计新的机器人。
当然,为了让这个题更加简单(否则怎么能叫水题欢乐赛呢),我们认为,这个机器人是由 Minecra? 里面的方块构成的。如果你不太明白这句话的意思,你可以认为在接下来的过程中,我们都不考虑重力所带来的影响,并且这个机器人全是由正六面体组成。于是,你为这个新的机器人画了一份草图,为了让更加标准化,你画了一个三视图。为了方便计算打印机所用的耗材,你将三视图的面积都分别计算了出来。很不幸的是,你一不小心把这个三视图弄丢了。于是,你的任务是重新构造这个立体图形。如果你,发现无法构造(这肯定是你的垃圾数学把面积算错了),你要悔过并输出我让你输出的东西。这会在下面的输出格式中提到。
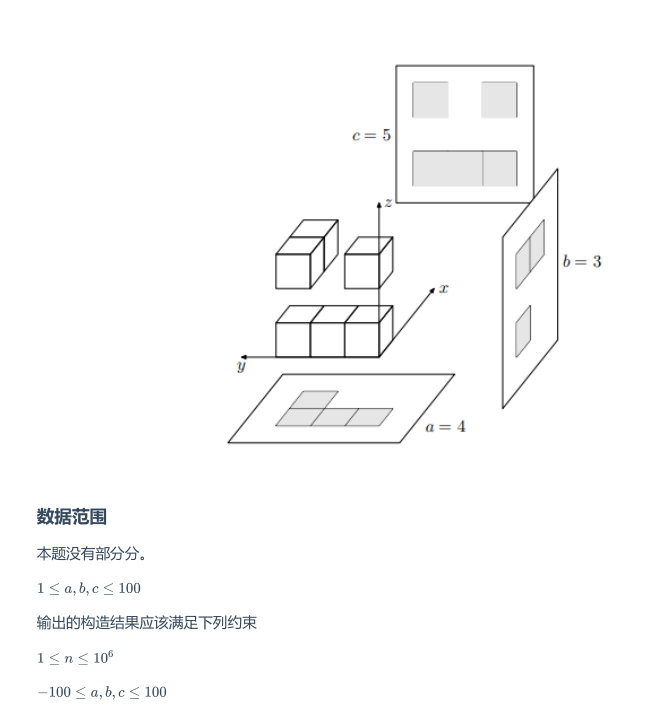
输入 ,分别表示三个视图的面积。具体是哪一个请看下面样例解释的图片
方块不受重力影响,且可以不连续
分析
构造题,又一次遇到了【上一次是暑假那个无耻的守夜问题,完全不知道怎么构造出来的】
先开始很在意这个正方体,其实发现好瓜啊,完全不必在意正方体,都说了不计重力
于是我就换了一个思路,想是不是让我构造点对,比如4 3 5 这个样例,就是构造4对(x,y),3对(x,y),5对(y,z)
然而每两对之间有限制条件,不是很好构造,每新加入一个数字,都会对两组点对的数量产生影响,除非这个数字以前出现过
这就是我的考场50分做法
就是从0 0 0,每次只改变一个数字,会使两组点对数量增加,当有点对为0的时候,在从以前选到过的中选两个一样的。
比如 1 0 0,1 0 1 ,0 0 1,这三组都选过了,我们选其他数字都会对两组点对数量产生影响,无法处理其他组已经不能再增加数量了,比如3对和4对已经选满了。
但我们可以选 0 1 1啊,这样只会对yz这一对造成影响,上面就是在讲这个意思。其实我觉得好好调一调是能当正解的
但是考场上我是真的没心情调,因为时间花得很厉害。。
100分做法
构造题==钻空子题
我们假设a<b<c,如果不是,swap一下
那么我们可以发现有解当前仅当 a*b>=c(就算a,b毫无重复都没有c那么多的面积,肯定是不合法的)
其实我们只需要构造一个平面图形啊!!!根本不需要三维
意思是,c所在的那一维不管
比如这个图 假设a==3,b==4,c==6,我们只需要构造一条斜线(红色的),不足面积b的地方也补齐(),然后再涂满c这么多面积就行了!!!
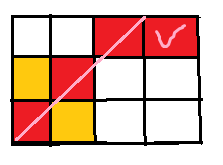 粉色的斜线已经粉色的补齐,黄色的是涂满
粉色的斜线已经粉色的补齐,黄色的是涂满
然后你会发现,这个图形的宽是3,从侧面看是3,长是4,从上面看是4,从正面看面积是6,当然,这是经过交换过后的,我们交换回去就好啦。
代码
#include<bits/stdc++.h> using namespace std; int cnt=0; struct email { int s,id; }a[5]; inline void print(int x,int y,int z) { int b[3]; b[a[0].id]=x,b[a[1].id]=y,b[a[2].id]=z; printf("%d %d %d ", b[0], b[1], b[2]); } bool cmp(email a,email b){return a.s<b.s;} int main() { for(int i=0;i<=2;i++)scanf("%d",&a[i].s),a[i].id=2-i; sort(a,a+3,cmp); if(a[0].s*a[1].s<a[2].s){puts("-1");return 0;} printf("%d ",a[2].s); for(int i=1;i<=a[1].s;i++) print(i,min(i,a[0].s),0),cnt++; for(int i=1;i<=a[1].s&&cnt<a[2].s;i++) for(int j=1;j<=a[0].s&&cnt<a[2].s;j++) if(j!=min(i,a[0].s)) print(i,j,0),cnt++; return 0; }