题面
波雷卡普有一个n×m,大小的棋盘,上面有k个车。他又放了q个矩形在上面。每一个矩形要受到保护。矩形受到保护的意思是对于该矩形内部所有的格子能够被这个矩形内的某个车攻击到或者被占据,和矩形外面的车无关,即矩形外面的车不能攻击到矩形里面。车的位置是固定的。1≤n,m≤100000, 1≤k,q≤200000.
分析
又是一道扫描线,还是很妙。
首先满足题意的情况只存在于矩形内每一行都有车或者每一列都有车,所以可以分行列来做,只要有其一满足就能满足。
就按列来讲,我们把车的纵坐标按照升序排序,竖着的扫描线每次移动到下一个区间的端点。
如何处理上下界呢?将区间也按上界升序排序,每次只把然后把这一段下面的点加入线段树维护,维护的是当前区间的纵坐标最小值。
如果区间高度最小小于了下界线,就是不合法的了。
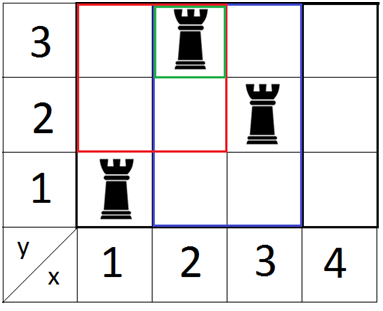
如图所示,遇到紫色矩形前,只维护了绿色空心车,然后遇到了紫色矩形的上界,上届向上移,加入了绿色实心的车。

因此,这一列上的绿色空心车的位置被更新到绿色实心车的位置。
同理,再处理行。
代码
#include<bits/stdc++.h> using namespace std; #define N 200200 #define lc (p<<1) #define rc (p<<1|1) #define mid (t[p].l+t[p].r>>1) #define INF 1234567890 int n,m,k,q; int ok[N]; struct e { int l,r,minx; }t[N*4]; struct ma { int x,y; }a[N]; struct il { int x1,y1,x2,y2,id; }b[N]; bool cmp1(ma a,ma b){return a.y<b.y;}; bool cmp2(il a,il b){return a.y2<b.y2;}; inline void pushup(int p) { t[p].minx=min(t[lc].minx,t[rc].minx); } inline void build(int p,int l,int r) { t[p].l=l;t[p].r=r; if(l==r) { t[p].minx=0; return ; } int bm=l+r>>1; build(lc,l,bm);build(rc,bm+1,r); pushup(p); } inline void update(int p,int x,int v) { if(t[p].l==t[p].r) { t[p].minx=v; return; } if(x<=mid)update(lc,x,v); if(x>mid)update(rc,x,v); pushup(p); } inline int query(int p,int ql,int qr) { int ret=INF; if(ql<=t[p].l&&qr>=t[p].r)return t[p].minx; if(ql<=mid)ret=min(ret,query(lc,ql,qr)); if(qr>mid)ret=min(ret,query(rc,ql,qr)); return ret; } void solve(int mx) { sort(a+1,a+1+k,cmp1);sort(b+1,b+1+q,cmp2); build(1,1,mx); int i=1,j=1; while(j<=q) { while(i<=k&&a[i].y<=b[j].y2)update(1,a[i].x,a[i].y),i++; if(query(1,b[j].x1,b[j].x2)>=b[j].y1)ok[b[j].id]=1;j++; } } int main() { scanf("%d%d%d%d",&n,&m,&k,&q); for(int i=1;i<=k;i++)scanf("%d%d",&a[i].x,&a[i].y); for(int i=1;i<=q;i++)scanf("%d%d%d%d",&b[i].x1,&b[i].y1,&b[i].x2,&b[i].y2),b[i].id=i; solve(n); for(int i=1;i<=k;i++)swap(a[i].x,a[i].y); for(int i=1;i<=q;i++)swap(b[i].x1,b[i].y1),swap(b[i].x2,b[i].y2); solve(m); for(int i=1;i<=q;i++) if(ok[i]) puts("YES"); else puts("NO"); return 0; }