DS博客作业07--查找
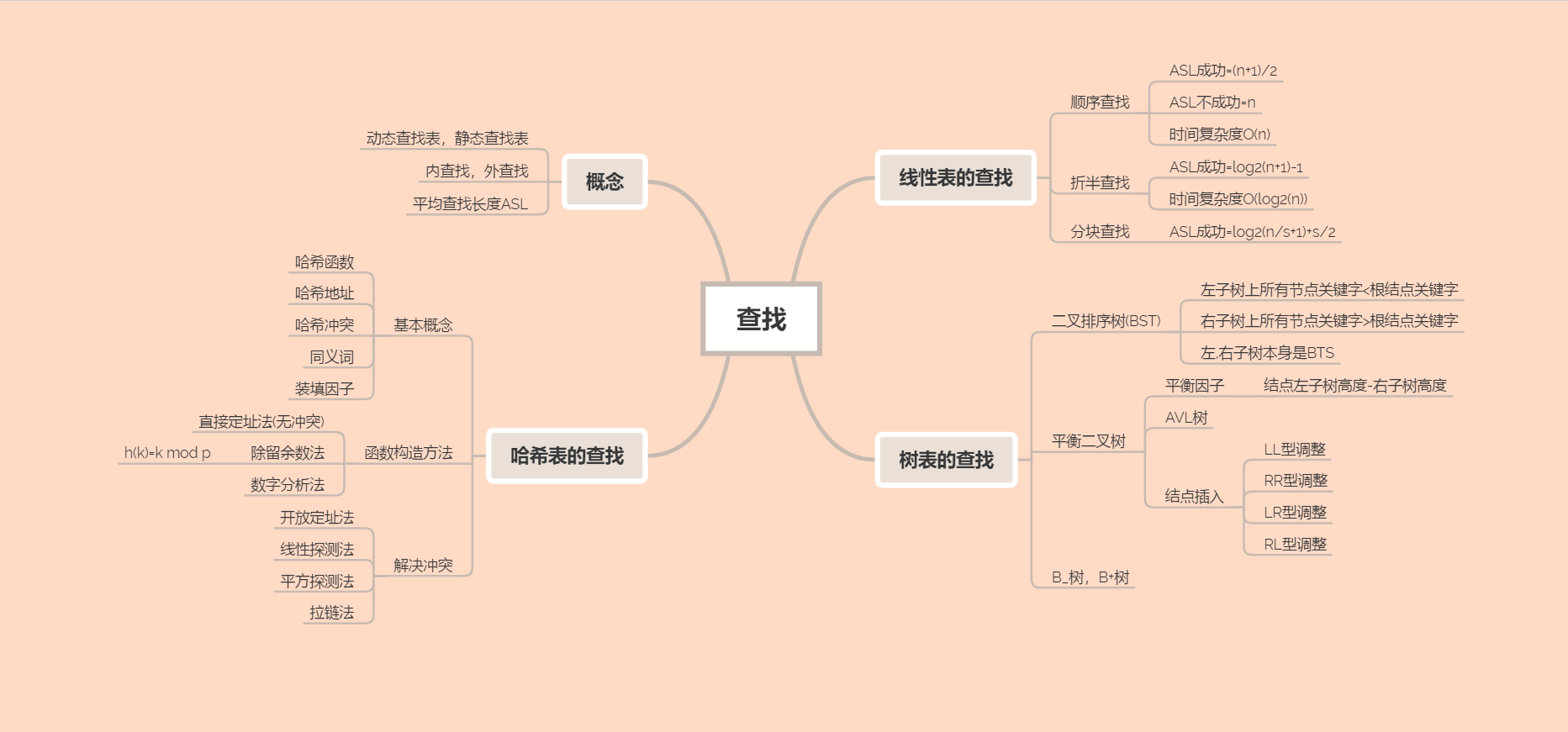
1.思维导图
2.对查找运算的认识及学习体会
- 这一周学习的查找里有很多关于前面线性表和树的知识,所以对基本概念的理解没有太大的问题。线性表的查找感觉理解和操作上面都更简单一些,其中顺序查找是比较熟悉的查找方法,折半查找也接触过,所以在线性表的查找上比较容易掌握。
- 二叉排序树难度比较大,首先是插入关键字的时候就必须注意,如果关键字插入就出现错误,那接下来对树的操作就会错误。树的另一个难点是平衡二叉树插入结点过程中的调整,虽然只有LL,RR,LR,RL四种调整,看课本也可以理解,但是当实际操作的时候还是难度比较大,必须先确定是插入的哪个结点导致了树的不平衡,然后再进行对应的调整方法。
- 哈希表在前面的pta题目里有使用过,具体的认识还是在这一章里,解决哈希冲突的线性探测法是第一次接触,用这个方法构造哈希表的时候要注意探测次数的统计,因为探测次数要用于接下来ASL的计算。
2.PTA实验作业
2.1.题目1: 二叉搜索树中的最近公共祖先
2.1.1设计思路
int find(Tree T,int n){
if T为空 返回0
if T->Key=n 返回1
else if T->Key>n
递归返回左子树
else 递归返回右子树
}
int LCA( Tree T, int u, int v ){
if T为空 返回ERROR
if u,v不在T中 返回ERROR
if u=T->Key或v=T->Key
返回T->Key
if u>T->Key且v<T->Key 或 u<T->Key且v>T->Key
返回T->Key
if u>T->Key 递归右子树
if u<T->Key 递归左子树
}
2.1.2代码截图

2.1.3本题PTA提交列表说明

Q1:忘记了如果u,v不在数中这个测试点
A1:加入find函数去寻找u,v是否在树中,问题解决。
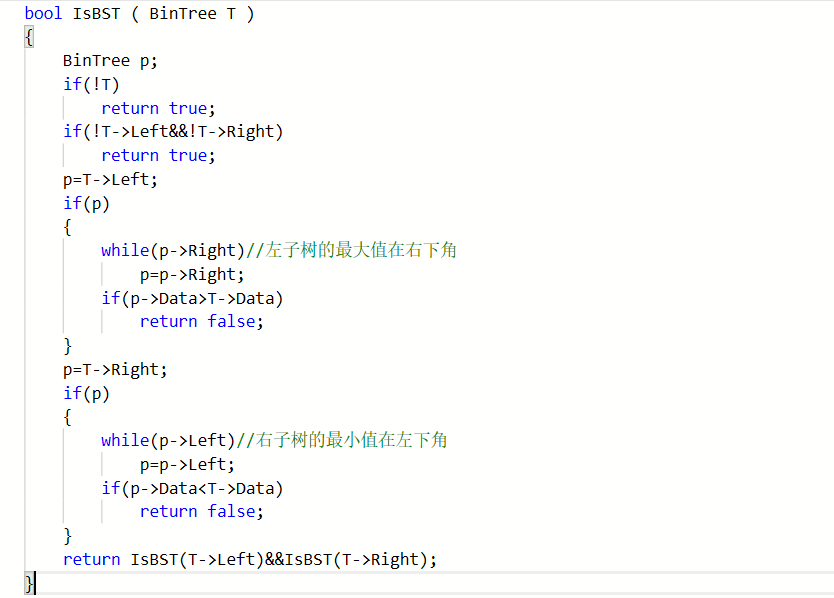
2.2 题目2:是否二叉搜索树
2.2.1设计思路
bool IsBST ( BinTree T )
{
创建新节点p
if T为空,返回true
if T左子树和右子树为空,返回true
p=T->Left
if p不为空
while(p->Right)
p=p->Right;
if (p->Data>T->Data)
返回false
end if
p=T->Right
if p不为空
while(p->Left)
p=p->Left;
if(p->Data<T->Data)
返回false
end if
返回 IsBST(T->Left)&&IsBST(T->Right);
}
2.2.2代码截图
2.2.3本题PTA提交列表说明

Q:没有考虑当左右子树都为二叉搜索树但答案为NO的情况
A:在左右子树判断正确后在和根结点进行一次比较,问题解决。
2.3 题目3:
2.3.1设计思路
2.3.2代码截图
2.3.3本题PTA提交列表说明
3、阅读代码
3.1 题目
在用除余法作为散列函数、线性探测解决冲突的散列表中,写一删除关键字的算法,要求将所有可以前移的元素前移去填充被删除的空位,以保证探测序列不致于断裂。
3.2 解题思路
首先计算关键字的散列地址,若该地址为空,则空操作;若该地址有关键字,但与给定值不等,则用解决冲突的方法去查找给定值;若该地址有关键字且与给定值相等,则实行删除。题目要求将所有可以前移的元素前移去填充被删除的空位,以保证探测序列不断裂。由于用线性探测解决冲突,设被删除元素的散列地址为i,则其余m-1(m为表长)个位置均可能是同义词。查找同义词的操作直到碰到空地址或循环一圈回到i才能结束。为了提高算法效率,减少数据移动,应将最后一个同义词前移填充被删除关键字。
3.3 代码截图

3.4 学习体会
这个题目因为用线性探测解决冲突,所以可能发生两个第一哈希地址不同的记录争夺同一后继哈希地址的情况。用上面的代码进行处理后,对于哈希地址为i的记录没有问题了,但由于将地址j置空,有可能截断了其它记录的探测通路。最明显的是哈希地址为j的记录就查不到了。解决的办法是继续调整,直到当前哈希表中的每个记录的查找都是正确的为止。