题意:构造一张N个结点无重边、无自环的无向图。使得其最小生成树和最大生成树共享K条边。
样例一很具有启发性:
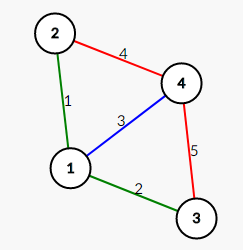
当K!=0时,我们可以先构造出一条链,链的长度为n-k的链,作为最小生成树的一部分,之后由点N向其他N-1个点连边,其中这N-1条边的边权严格大于之前N-K-1条边的。这样可以保证最大生成树与最小生成树共享了那N-1条边中的K条。
当K=0时,依照以上方法构造会出现重边。其实也很简单,先以小权值将N个点串成一条链。再将1向3~n连边,最后将2、4连边即可。
#include<bits/stdc++.h> using namespace std; int n,k; int main(){ scanf("%d%d",&n,&k); if(k>=n||((n==2||n==3)&&k==0)){printf("-1 ");return 0;} int cnt=0;cnt++; if(k==0){ printf("%d ",2*n-2); for(int i=1;i<n;i++,cnt++)printf("%d %d %d ",i,i+1,cnt); for(int i=3;i<=n;i++,cnt++)printf("1 %d %d ",i,cnt); printf("2 4 %d ",cnt); return 0; } printf("%d ",2*n-k-2); for(int i=1;i<=n-k-1;i++,cnt++)printf("%d %d %d ",i,i+1,cnt); for(int i=1;i<=n-1;i++,cnt++)printf("%d %d %d ",n,i,cnt); return 0; }