在《具体数学》4.5中看到了SB-Tree,觉得非常有趣,就去研究了一下。
首先介绍一下Stern-Brocot Tree。Stern-Brocot Tree是一种能将所有的最简分数都表示出来的结构,这不禁令人联想到一种在NOIP中曾出现的Cantor表,但注意,Contor表所表示的并不全是最简分数。
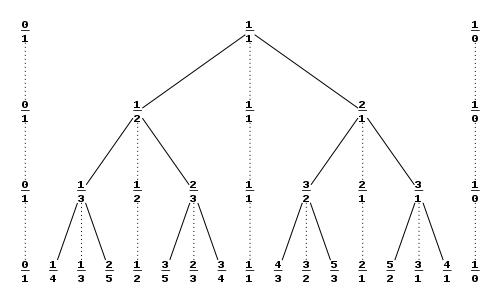
图1:Stern-Brocot Tree
观察SB-Tree的结构,我们可以很快发现它的构造方式,即从(0/1,1/0)出发,在两个相邻的分数m/n和m'/n'中插入(m+m')/(n+n'),这个插入的数我们称作m/n和m'/n'的中位分数(mediant)。
根据这棵树的构造方式,我们不难发现,均有:m'n-mn'=1,当插入一个新的中值分数时,都满足:(m+m')n-m(n+n')=1且m'(n+n')-(m+m')n'=1。那么这棵树中的所有m,n,都必须满足(m,n)=1
那么会否遗漏呢?答案是不会的,在《具体数学》中给出了一种证明,在此不多赘述。
Stern-Brocot Tree还与一种有趣的级数列相关:法里级数(Farey serires)。法里级数是介于0和1之间分母不超过N的所有最简分数的集合,且按照递增的次序排序。

图2:Farey serires
wiki上给出了它与几何的一种优美的联系,如下:
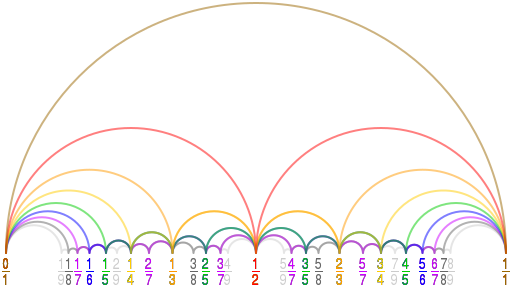
图3:Farey diagram
如果仔细观察SB-Tree,我们就可以发现,每一阶的法里级数均是SB-Tree的子树。那么,法里级数的构造方法也就显而易见了,即在相邻的分数m/n和m'/n'中插入(m+m')/N。
法里级数有一些基于此的奇奇怪怪的应用,有空补上。
回到Stern-Brocot Tree。我们已经证明了SB Tree可以当作一个有理数的数系。那么每一个有理数都将对应一条唯一从根结点开始的树上路径,每一条从根结点开始的树上路径也将对应一个唯一的有理数。我们考虑怎么找到路径对应的数或者数所对应的路径。
首先可以证明SB Tree是一棵排序二叉树,我写出自己对某个节点左子树的证明(既然是我自己口胡的,那就不一定对嘛23333):
假设节点A对应的有理数为a/b,那么在他的左子树中,某一层最大的节点必为最靠右,设为B,的那个,设之为c/d。根据SB Tree的生成方式,它的下一层最靠右的节点为(c+a)/(b+d),化简后可以发现,它与a/b>c/d是等价的,因为B在在A的左子树中,那么上式必定成立。
右子树的证明也将类似,不多赘述。
那么我们就可以按照在排序二叉树中寻找元素的方式寻找相应的有理数了,但冷静的思考后我们会发现生成一棵完整的SB-Tree并不是一件容易的事情。
我们能否在不求出所有节点的情况下解决问题呢?
我们定义一个路径的表示为一个由L和R组成的字符串,顾名思义,L表示进入左子树,R表示进入右子树。令,f(s)表示串s对应的有理数。如f(LRRL)=5/7
观察f(s)的数学性质我们可以得出(作者语,观察你个头。。。)2*2的01矩阵可以很好的得出f(s)的数学表示。定义M(s)为s所对应得矩阵,则有:


那么对于任意一个路径譬如:
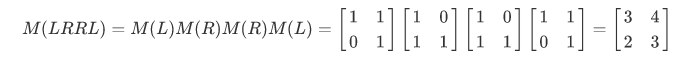
那么:
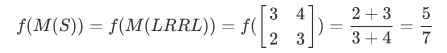
更一般的形式为:
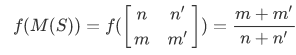
那么我们就可以通过矩阵来进行二叉搜索,或者推出路径所对应的有理数,如下:
S:=I; while m/n<>f(S) do if m/n<f(S) then (output(L);S:=SL;) else (output(R);S:=SR;)
但矩阵运算毕竟较为麻烦,我们考虑更简单的方法。
首先我们可以发现:
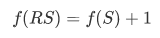
由是可以得出:
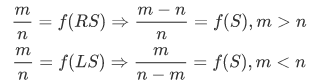
于是就可以如是二叉搜索:
while m<>n do if m<n then (output(L);n:=n-m;) else (output(R);m:=m-n;)
这样的操作比起矩阵有个更大的好处,它可以快速找出逼近某个无理数的有理数,将if语句改一下即可:
if a<1 then (output(L);a:=a/(1-a);) else (output(R);a:=a-1;)
我们考虑用SB Tree来构造一些问题(我胡诌的。。。)
1.已知两个有共同父亲的节点,求他们的父亲:
通过矩阵运算列一个四元方程直接求解即可。
2.求N个节点的LCA:
求出所有节点的S串,找最长公共前缀即可。(当然这个算法是有优化空间的)
3.第N层分母分子小于均等于N的数有多少(HDU4556)
phi(n)的前缀和*2即可
4.不用高精乘的有理数比较(无聊。。。)
比较两个有理数路径的字典序即可
不玩了,干正事去。。。。