问题描述:
二维平面上n个点,要求找出距离最近的两个点之间的距离。
解决流程:
将点对按照x坐标升序排列,x相同时按照y升序排列
从中间那个点pmid,将点集P分为P1和P2
递归P1和P2,找到它们中的最近点对的距离d1,d2,d=min(d1, d2)
判断P1和P2之间有没有更近的点对,可能的点对在[pmid.x-d, pmid.x+d]这个长条状区域内,记作PP(p possible)
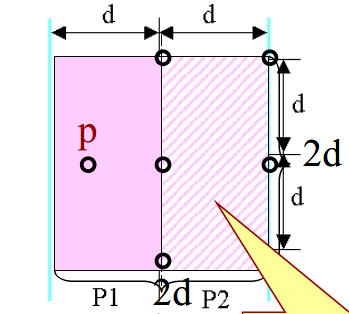
对每一个p1∈P1∩PP,发现可能的p2都在分界线右侧d*2d的范围内。实际应该是(pmid.x, p1.y)为圆心,半径为d的半圆,不过取矩形或许是为了方便?
可以知道,右侧矩形范围中满足条件的p2不超过6个,由此可知,我们只需检验6*n/2次即可确,检验的复杂度为O(n)
(证明:
将矩形等分成6分,变成(d/2)*(2*d/3)的矩形
如果一个小矩形中包含2个可能的点,那么它们的距离必定小于这个矩形对角线的距离5d/6
又因为P2中的点的最小距离为必定大于等于d
所以一个小矩形不可能包含两个以上的点
)
因为是不断二分,所以算法复杂度为O(n*lgn)