BZOJ2132 圈地计划 【最小割】

题目

最近房地产商GDOI(Group of Dumbbells Or Idiots)从NOI(Nuts Old Idiots)手中得到了一块开发土地。据了解，
这块土地是一块矩形的区域，可以纵横划分为N×M块小区域。GDOI要求将这些区域分为商业区和工业区来开发。根
据不同的地形环境，每块小区域建造商业区和工业区能取得不同的经济价值。更具体点，对于第i行第j列的区域，
建造商业区将得到Aij收益，建造工业区将得到Bij收益。另外不同的区域连在一起可以得到额外的收益，即如果区
域(I,j)相邻（相邻是指两个格子有公共边）有K块（显然K不超过4）类型不同于(I,j)的区域，则这块区域能增加k
×Cij收益。经过Tiger.S教授的勘察，收益矩阵A,B,C都已经知道了。你能帮GDOI求出一个收益最大的方案么？

输入格式

输入第一行为两个整数，分别为正整数N和M，分别表示区域的行数和列数；
第2到N+1列，每行M个整数，表示商业区收益矩阵A；
第N+2到2N+1列，每行M个整数，表示工业区收益矩阵B；
第2N+2到3N+1行，每行M个整数，表示相邻额外收益矩阵C。
任何数字不超过1000”的限制

输出格式

输出只有一行，包含一个整数，为最大收益值。

输入样例

3 3

1 2 3

4 5 6

7 8 9

9 8 7

6 5 4

3 2 1

1 1 1

1 3 1

1 1 1

输出样例

81

提示

【数据规模】

对于100%的数据有N,M≤100

题解

类似BZOJ2127happiness
上一次似乎没有写博，，

一个经典的最小割模型，每个人有两个选择，每个选择有不同收益，当一些人选择相同时会有额外的收益，求最大收益
用一个这样的图：

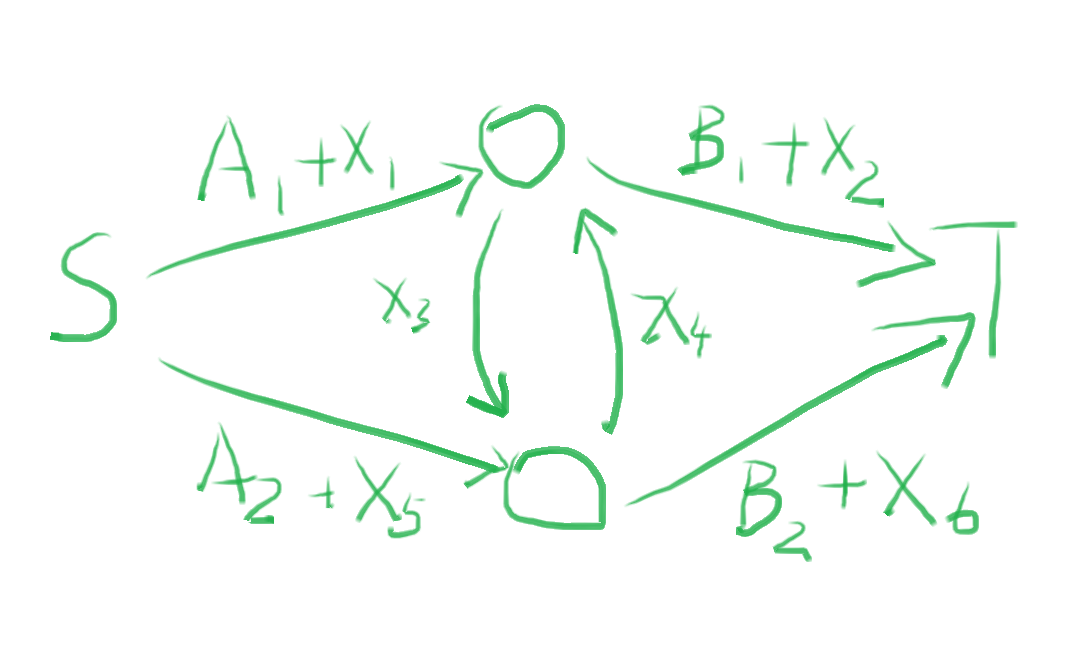
这个图有两种割法
设二人同选(A)的额外收益为(w_a)，同选(B)为(w_b)
①当二者选择不同时，除了没选的收益外，会付出额外代价(w_a + w_b)
对应的图中代价，要割掉不同侧的边，以及中间的一条边

[x_1 + x_3 + x_6 ]

[x_2 + x_4 + x_5 ]

②选择相同时，除了
对应图中，割掉一侧的边即可

[x_1 + x_5 ]

[x_2 + x_6 ]

那么有：

[x_1 + x_3 + x_6 = w_a + w_b ]

[x_2 + x_4 + x_5 = w_a + w_b ]

[x_1 + x_5 = w_b ]

[x_2 + x_6 = w_a ]

似乎有多解，我们不妨设：

[x_1 = x_5 ]

[x_2 = x_6 ]

即可得到一组比较特殊的解：

[x_1 = x_5 = frac{w_b}{2} qquad x_2 = x_6 = frac{w_a}{2} qquad x_3 = x_4 = frac{w_a + w_b}{2} ]

那么最小割即为在提前拥有所有收益后必须付出的最小代价了

具体建图中，我们通常将边权乘(2)变为整数

回到这题，建图就很裸了
不过这题是不同产生收益，我们二分染色一下，然后对于其中一种颜色的点(AB)交换即可

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 10005,maxm = 200005,N = 105,INF = 1000000000;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
int A[N][N],B[N][N],C[N][N],id[N][N],X[4] = {0,0,-1,1},Y[4] = {-1,1,0,0};
int n,m,S,T;
int h[maxn],ne = 2;
struct EDGE{int to,nxt,f;}ed[maxm];
inline void build(int u,int v,int w){
	ed[ne] = (EDGE){v,h[u],w}; h[u] = ne++;
	ed[ne] = (EDGE){u,h[v],0}; h[v] = ne++;
}
int d[maxn],vis[maxn],used[maxn],cur[maxn],now;
int q[maxn],head,tail;
inline bool bfs(){
	q[head = tail = 1] = S; vis[S] = now; d[S] = 0;
	int u;
	while (head <= tail){
		u = q[head++];
		Redge(u) if (ed[k].f && vis[to = ed[k].to] != now){
			d[to] = d[u] + 1; vis[to] = now;
			if (to == T) return true;
			q[++tail] = to;
		}
	}
	return vis[T] == now;
}
int dfs(int u,int minf){
	if (u == T || !minf) return minf;
	int flow = 0,f,to;
	if (used[u] != now) cur[u] = h[u],used[u] = now;
	for (int& k = cur[u]; k; k = ed[k].nxt)
		if (vis[to = ed[k].to] == now && d[to] == d[u] + 1 && (f = dfs(to,min(minf,ed[k].f)))){
			ed[k].f -= f; ed[k ^ 1].f += f;
			flow += f; minf -= f;
			if (!minf) break;
		}
	return flow;
}
int maxflow(){
	int flow = 0; now = 1;
	while (bfs()){
		flow += dfs(S,INF);
		now++;
	}
	return flow;
}
int main(){
	n = read(); m = read(); S = 0; T = m * n + 1;
	int ans = 0;
	REP(i,n) REP(j,m) A[i][j] = read(),ans += A[i][j],A[i][j] <<= 1;
	REP(i,n) REP(j,m) B[i][j] = read(),ans += B[i][j],B[i][j] <<= 1;
	REP(i,n) REP(j,m) C[i][j] = read();
	REP(i,n) REP(j,m) id[i][j] = (i - 1) * m + j;
	REP(i,n) REP(j,m){
		int x,y,tmp;
		if ((i & 1) ^ (j & 1)){
			for (int k = 0; k < 4; k++){
				x = i + X[k];
				y = j + Y[k];
				if (x < 1 || y < 1 || x > n || y > m) continue;
				tmp = C[i][j] + C[x][y]; ans += tmp << 1;
				A[i][j] += tmp; B[i][j] += tmp;
				A[x][y] += tmp; B[x][y] += tmp;
				build(id[i][j],id[x][y],tmp << 1);
				build(id[x][y],id[i][j],tmp << 1);
			}
		}
	}
	REP(i,n) REP(j,m){
		if ((i & 1) ^ (j & 1)){
			build(S,id[i][j],A[i][j]);
			build(id[i][j],T,B[i][j]);
		}
		else {
			build(S,id[i][j],B[i][j]);
			build(id[i][j],T,A[i][j]);
		}
	}
	printf("%d
",ans - (maxflow() >> 1));
	return 0;
}