题目
如果一个字符串可以被拆分为 AABBAABB 的形式,其中 AA 和 BB 是任意非空字符串,则我们称该字符串的这种拆
分是优秀的。例如,对于字符串 aabaabaa,如果令 A=aabA=aab,B=aB=a,我们就找到了这个字符串拆分成 AABBA
ABB 的一种方式。一个字符串可能没有优秀的拆分,也可能存在不止一种优秀的拆分。比如我们令 A=aA=a,B=baa
B=baa,也可以用 AABBAABB 表示出上述字符串;但是,字符串 abaabaa 就没有优秀的拆分。现在给出一个长度为
nn 的字符串 SS,我们需要求出,在它所有子串的所有拆分方式中,优秀拆分的总个数。这里的子串是指字符串
中连续的一段。以下事项需要注意:出现在不同位置的相同子串,我们认为是不同的子串,它们的优秀拆分均会被
记入答案。在一个拆分中,允许出现 A=BA=B。例如 cccc 存在拆分 A=B=cA=B=c。字符串本身也是它的一个子串。
输入格式
每个输入文件包含多组数据。输入文件的第一行只有一个整数 TT,表示数据的组数。保证 1≤T≤101≤T≤10。接
下来 TT 行,每行包含一个仅由英文小写字母构成的字符串 SS,意义如题所述。
输出格式
输出 TT 行,每行包含一个整数,表示字符串 SS 所有子串的所有拆分中,总共有多少个是优秀的拆分。
输入样例
4
aabbbb
cccccc
aabaabaabaa
bbaabaababaaba
输出样例
3
5
4
7
提示
我们用 S[i,j]S[i,j] 表示字符串 SS 第 ii 个字符到第 jj 个字符的子串(从 11 开始计数)。第一组数据中,
共有 33 个子串存在优秀的拆分:S[1,4]=aabbS[1,4]=aabb,优秀的拆分为 A=aA=a,B=bB=b;S[3,6]=bbbbS[3,6]
=bbbb,优秀的拆分为 A=bA=b,B=bB=b;S[1,6]=aabbbbS[1,6]=aabbbb,优秀的拆分为 A=aA=a,B=bbB=bb。而剩
下的子串不存在优秀的拆分,所以第一组数据的答案是 33。第二组数据中,有两类,总共 44 个子串存在优秀的
拆分:对于子串 S[1,4]=S[2,5]=S[3,6]=ccccS[1,4]=S[2,5]=S[3,6]=cccc,它们优秀的拆分相同,均为 A=cA=c,
B=cB=c,但由于这些子串位置不同,因此要计算 33 次;对于子串 S[1,6]=ccccccS[1,6]=cccccc,它优秀的拆分
有 22 种:A=cA=c,B=ccB=cc 和 A=ccA=cc,B=cB=c,它们是相同子串的不同拆分,也都要计入答案。所以第二组
数据的答案是 3+2=53+2=5。第三组数据中,S[1,8]S[1,8] 和 S[4,11]S[4,11] 各有 22 种优秀的拆分,其中 S[1
,8]S[1,8] 是问题描述中的例子,所以答案是 2+2=42+2=4。第四组数据中,S[1,4]S[1,4],S[6,11]S[6,11],S[7
,12]S[7,12],S[2,11]S[2,11],S[1,8]S[1,8] 各有 11 种优秀的拆分,S[3,14]S[3,14] 有 22 种优秀的拆分,
所以答案是 5+2=75+2=7。
题解
我们设(f[i])为以(i)为结尾的(AA)串的数量
设(g[i])为以(i)开头的(AA)串的数量
那么
所以我们只要找出所有(AA)串即可
根据后缀数组的套路,为找出所有(AA)串,我们枚举(A)的长度(L),然后每隔(L)设一个监测点,如图:
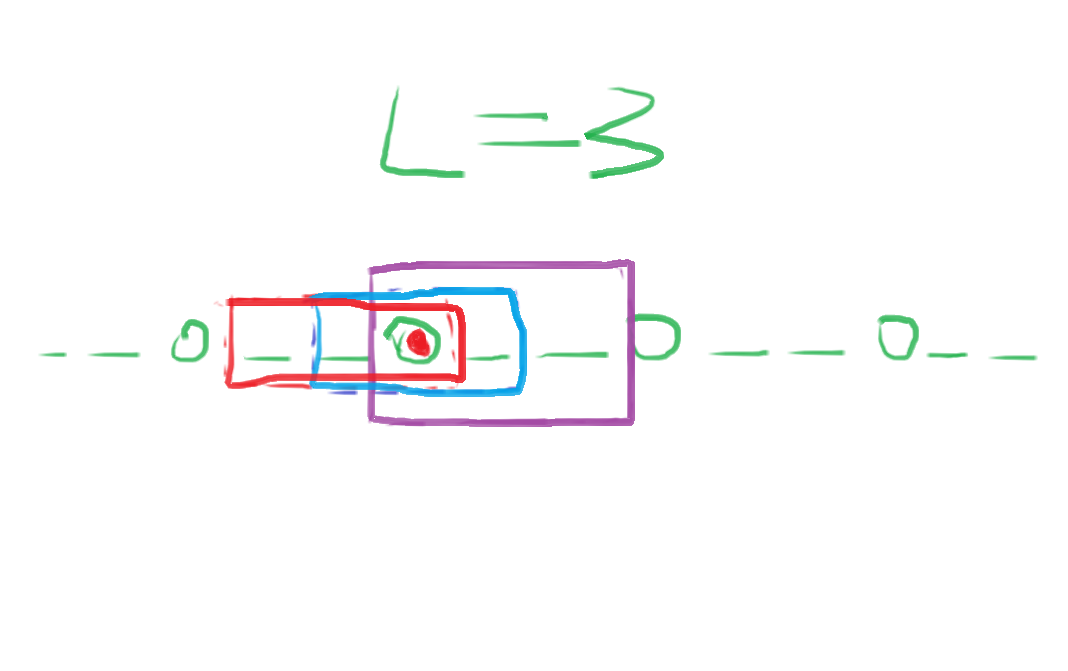
其中圈起来的就是中间那个监测点所管辖的(len = 3)的子串
如此,如果存在长度为(2 * L)的(AA)串,那么相邻的(A)中一定有且仅有一个相邻的监测点
我们就枚举相邻的两个监测点,比较它们的lcp和往前的lcp大小,就可以确定它们管辖的串那些可以匹配
具体对正串反串分别求一次SA【或者并在一起求】,做到(O(1))询问lcp
然后用一个差分数组维护(f[i])和(g[i])
最后统计答案就做完了
时间复杂度(O(nlogn + sumlimits_{L = 1}^{n} frac{n}{L}) = O(nlogn + n * sumlimits_{L = 1}^{n} frac{1}{L}) = O(nlogn))
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define cls(s) memset(s,0,sizeof(s))
using namespace std;
const int maxn = 100005,maxm = 100005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
char s[maxn];
int N,n,m,sa[maxn],rank[maxn],height[maxn],t1[maxn],t2[maxn],bac[maxn];
int mn[maxn][18],bin[30],Log[maxn];
void getsa(){
int *x = t1,*y = t2; m = 1000;
for (int i = 0; i <= m; i++) bac[i] = 0;
for (int i = 1; i <= n; i++) bac[x[i] = s[i]]++;
for (int i = 1; i <= m; i++) bac[i] += bac[i - 1];
for (int i = n; i; i--) sa[bac[x[i]]--] = i;
for (int k = 1; k <= n; k <<= 1){
int p = 0;
for (int i = n - k + 1; i <= n; i++) y[++p] = i;
for (int i = 1; i <= n; i++) if (sa[i] - k > 0) y[++p] = sa[i] - k;
for (int i = 0; i <= m; i++) bac[i] = 0;
for (int i = 1; i <= n; i++) bac[x[y[i]]]++;
for (int i = 1; i <= m; i++) bac[i] += bac[i - 1];
for (int i = n; i; i--) sa[bac[x[y[i]]]--] = y[i];
swap(x,y);
x[sa[1]] = p = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k] ? p : ++p);
if (p >= n) break;
m = p;
}
for (int i = 1; i <= n; i++) rank[sa[i]] = i;
for (int i = 1,k = 0; i <= n; i++){
if (k) k--;
int j = sa[rank[i] - 1];
while (s[i + k] == s[j + k]) k++;
height[rank[i]] = k;
}
for (int i = 1; i <= n; i++) mn[i][0] = height[i];
REP(j,17) REP(i,n){
if (i + bin[j] - 1 > n) break;
mn[i][j] = min(mn[i][j - 1],mn[i + bin[j - 1]][j - 1]);
}
}
int lcp(int a,int b){
int l = rank[a],r = rank[b];
if (l > r) swap(l,r); l++;
int t = Log[r - l + 1];
return min(mn[l][t],mn[r - bin[t] + 1][t]);
}
int pre_lcp(int a,int b){
int l = rank[N - a + 1],r = rank[N - b + 1];
if (l > r) swap(l,r); l++;
int t = Log[r - l + 1];
return min(mn[l][t],mn[r - bin[t] + 1][t]);
}
LL f[maxn],g[maxn];
void solve(){
memset(f,0,sizeof(f));
memset(g,0,sizeof(g));
for (int L = 1; L <= (n >> 1); L++){
for (int a = L,b = a + L,l,r,lenl,lenr,len; b <= n; a += L,b += L){
lenl = min(pre_lcp(a,b),L);
lenr = min(lcp(a,b),L);
len = lenl + lenr - 1;
l = a - lenl + 1; r = l + len - L;
if (l <= r) g[l]++,g[r + 1]--;
l = b - lenl + L; r = l + len - L;
if (l <= r) f[l]++,f[r + 1]--;
}
}
REP(i,n) g[i] += g[i - 1],f[i] += f[i - 1];
//REP(i,n) printf("%lld",f[i]); puts("");
//REP(i,n) printf("%lld",g[i]); puts("");
LL ans = 0;
for (int i = 2; i < n - 1; i++){
ans += f[i] * g[i + 1];
}
printf("%lld
",ans);
}
int main(){
bin[0] = 1; for (int i = 1; i <= 25; i++) bin[i] = bin[i - 1] << 1;
Log[0] = -1; for (int i = 1; i < maxn; i++) Log[i] = Log[i >> 1] + 1;
int T = read();
while (T--){
cls(s); cls(t1); cls(t2);
scanf("%s",s + 1); n = strlen(s + 1);
s[n + 1] = '#';
for (int i = 1; i <= n; i++) s[n + 1 + i] = s[n - i + 1];
N = n = n << 1 | 1;
getsa();
n >>= 1;
solve();
}
return 0;
}