洛谷P1268 树的重量 【构造 + 枚举】

题目描述

树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树，其叶节点表示一个物种，两个叶节点之间的距离表示两个物种的差异。现在，一个重要的问题是，根据物种之间的距离，重构相应的“进化树”。

令N={1..n}，用一个N上的矩阵M来定义树T。其中，矩阵M满足：对于任意的i，j，k，有M[i,j] + M[j,k] >= M[i,k]。树T满足：

1．叶节点属于集合N；

2．边权均为非负整数；

3．dT(i,j)=M[i,j]，其中dT(i,j)表示树上i到j的最短路径长度。

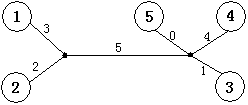
如下图，矩阵M描述了一棵树。

树的重量是指树上所有边权之和。对于任意给出的合法矩阵M，它所能表示树的重量是惟一确定的，不可能找到两棵不同重量的树，它们都符合矩阵M。你的任务就是，根据给出的矩阵M，计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树，这棵树的总重量为15。

输入输出格式

输入格式：

输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-l行，给出的是矩阵M的一个上三角(不包含对角线)，矩阵中所有元素是不超过100的非负整数。输入数据保证合法。

输入数据以n=0结尾。

输出格式：

对于每组输入，输出一行，一个整数，表示树的重量。

输入输出样例

输入样例#1：

5
5 9 12 8
8 11 7
5 1
4
4
15 36 60
31 55
36
0

输出样例#1：

15
71

题解

这道题用了构造的思想。想了很久想不出来，看了题解恍然大悟。

首先如果只有两个点，那么原树就是两个点用他们之间长度的边连起来。【这个很好想到吧】

这个时候我们多了一个点，试想这个点放在哪？

原来的两点已经满足了条件，我们可以不用考虑，我们尝试从两点之间的路径上分出一个分支来插入第三个节点，如图所示：

很容易这样一来，新插入的边长就为(d[1][3] + d[2][3] - d[1][2]) / 2

第四个点呢？

那我们就尝试插入1,3之间,2,3之间1,2之间

对于第i个点就枚举前i-1个点，尝试插入两两之间，选择最小的方案作为最后的答案

就搞完啦~

代码异常的短。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long int
using namespace std;
const int maxn = 35,maxm = 100005,INF = 2000000000;

int d[maxn][maxn];

int main(){
	int n,ans,t;
	while (~scanf("%d",&n) && n){
		for (int i = 1; i <= n; i++)
			for (int j = i + 1; j <= n; j++)
				scanf("%d",&d[i][j]);
		ans = d[1][2];
		for (int i = 3; i <= n; i++){
			t = INF;
			for (int j = 1; j < i; j++)
				for (int k = j + 1; k < i; k++){
					t = min(t,(d[j][i] + d[k][i] - d[j][k]) / 2);
				}
			ans += t;
		}
		printf("%d
",ans);
	}
	return 0;
}