1.dijkstra算法
dijkstra是一个从单个源到所有源的最短路径的贪心算法,即每次找出最有利的解,合起来就是最优解。
假如现在有一个图如下,
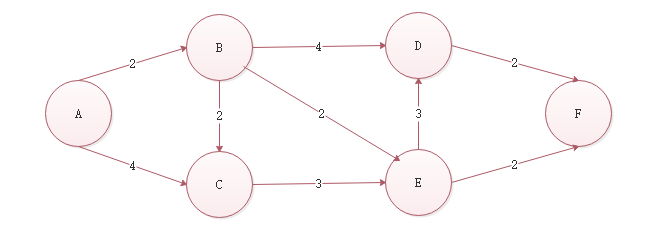
首先,我们先用一个数组来表示A顶点到各个其他顶点之间的距离,
var graph = [ [0, 2, 4, 0, 0, 0], [0, 0, 2, 4, 2, 0], [0, 0, 0, 0, 3, 0], [0, 0, 0, 0, 0, 2], [0, 0, 0, 3, 0, 2], [0, 0, 0, 0, 0, 0] ]
算法描述
首先先从A节点出发,标示A已经遍历,这样下次就不用遍历A这个节点,找到B,记录到B的距离,找到C,记录到C的距离
然后找出A到B和C之间距离最短的节点,B;
然后从B点出发,标示B已经遍历,记录B到C,D,E的最短距离,找出距离最短的节点C,
然后从C点出发,标示C已经遍历,找到E,但是A->B->C->E的距离大于A->B->E的距离,所以这里就记录A->B->C->E的距离
然后从D点出发,标示D已经遍历,记录D到F的最短距离,
然后从E点出发,标示E已经遍历,记录E到D和F的最短距离,因为A->B->E->D大于A->B->D的距离,所以这里不记录A->B->E->D的距离,但是A->B->E->F的距离是小于A->B->D->F的距离,所以记录A->B->E->F的距离
var graph = [ [0, 2, 4, 0, 0, 0], [0, 0, 2, 4, 2, 0], [0, 0, 0, 0, 3, 0], [0, 0, 0, 0, 0, 2], [0, 0, 0, 3, 0, 2], [0, 0, 0, 0, 0, 0] ] function dijstra(graph,src){ const dist = [];//用来记录,一点源点,到其他顶点的距离的数组。 const visited = [];//用来表示已经访问的节点。 const INF = Number.MAX_SAFE_INTEGER; //初始化数组 for(let i = 0; i < graph.length; i++){ dist[i] = INF; visited[i] = false; } let a = 0;//用来记录遍历的数量 dist[src] = 0; while(a < graph.length-1){ let edg = graph[src]; visited[src] = true; for(let j = 0; j < edg.length; j++){ if(edg[j] !== 0){ if(dist[src] + edg[j] < dist[j]){//记录最短路径 dist[j] = dist[src] + edg[j];//更新最短路径 } } } let min = INF; let minIndex = -1; //选出路径最短的节点,并且下一轮循环从这节点开始 for(let b = 0; b < dist.length; b++){ if(!visited[b]&&dist[b]<min){ min = dist[b]; minIndex = b; } } src = minIndex; a++; } return dist; } console.log(dijstra(graph,0));//[ 0, 2, 4, 6, 4, 6 ]
2.floyd算法
const INF = Number.MAX_SAFE_INTEGER var graph = [ [0, 2, 4, 0, 0, 0], [0, 0, 2, 4, 2, 0], [0, 0, 0, 0, 3, 0], [0, 0, 0, 0, 0, 2], [0, 0, 0, 3, 0, 2], [0, 0, 0, 0, 0, 0] ] function initializeGraph(graphArr){ let length = graphArr.length; let cost = []; for(let i = 0; i < length; i++){ cost[i] = []; for(let j = 0; j < length; j++){ if(graphArr[i][j] == 0){ cost[i][j] = INF; }else{ cost[i][j] = graphArr[i][j]; } } } return cost; } function floyd(graph){ let cost = initializeGraph(graph); let length = graph.length; let dist = []; for(let i = 0; i < length; i++){ dist[i] = []; for(let j = 0; j < length; j++){ if(i == j){ dist[i][j] = 0; }else{ dist[i][j] = cost[i][j]; } } } for(let k =0; k < length; k++){ for(let i = 0; i < length; i++){ for(let j = 0; j < length; j++){ if(dist[i][k]+dist[k][j] < dist[i][j]){ dist[i][j] = dist[i][k]+dist[k][j]; } } } } return dist[0]; } console.log(floyd(graph));