• K：二叉查找树(BST)

    相关介绍:

     二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树（英语：ordered binary tree），排序二叉树（英语：sorted binary tree），二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。

    二叉查找树的定义：

     二叉查找树或者是一棵空树，或者是一棵具有以下性质的二叉树:

    1. 当左子树不为空，则左子树上所有节点的值均小于根节点的值

    2. 当右子树不为空，则右子树上所有节点的值均大于根节点的值

    3. 它的左右子树也都是二叉查找树

    下图显示的二叉树便是一棵二叉查找树：

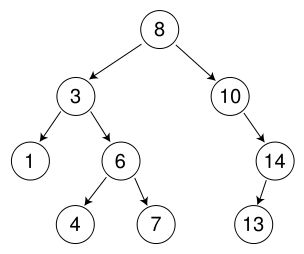
    二叉查找树的例子示意图

    有趣的是，对二叉查找树进行中序遍历，得到的结果，其是一个按照关键字有序的记录序列

    二叉查找树的相关知识点：

     对于二叉查找树，其主要的方法是查找、插入、删除相关的节点，以下介绍其相关的操作过程及给出相应的代码，在给出相关的操作之前，给出相关节点类的代码描述

    二叉查找树的节点类：

    /**
 * 二叉查找树的相关节点类
 * @author 学徒
 *
 */
class BinarySearchTreeNode
{
	//节点的左子树指针
	BinarySearchTreeNode left;
	//节点的右子树指针
	BinarySearchTreeNode right;
	//关键字值
	Comparable key;
	//该节点的相关数据
	Object data;
	public BinarySearchTreeNode(BinarySearchTreeNode left,BinarySearchTreeNode right,Comparable key,Object data)
	{
		this.left=left;
		this.right=right;
		this.key=key;
		this.data=data;
	}
	public BinarySearchTreeNode(Comparable key,Object data)
	{
		this(null,null,key,data);
	}
}

    二叉查找树的查找过程：

     若将查找表组织为一棵二叉查找树，则根据二叉查找树的特点，查找过程的主要步骤归纳如下：

    1. 若查找树为空，则查找失败
    2. 若查找树非空，则
      1. 若给定值k等于根节点的关键字值，则查找成功，结束查找过程，否则转步骤2
      2. 若给定值k小于根节点的关键字值，则继续在根节点的左子树上进行，否则转3
      3. 若给定值k大于根节点的关键字值，则继续在根节点的右子树上进行

    相关代码：

    /**
 * 二叉查找树的查找操作
 * @param data 需要进行查找的相关数据
 * @return 查找到的相关的结果，当查找失败时，返回null
 */
public Object search(Comparable key)
{
	if(key==null)
	{
		return null;
	}
	return toSearch(root,key);
}
/**
 * 在二叉查找树中进行递归的查找的方法
 * @param data 需要进行查找的数据
 * @param node 二叉树中某个子树的根节点
 * @return 查找的节点类的结果
 */
private Object toSearch(BinarySearchTreeNode node,Comparable key)
{
	if(node==null)
	{
		return null;
	}
	//与根节点的相关值进行比较并选择合适的分支
	int compara=node.key.compareTo(key);
	if(compara==0)
		return node.data;
	else if(compara<0)
		return toSearch(node.right,key);
	else
		return toSearch(node.left,key);
}

    二叉查找树的插入操作：

     二叉查找树中，插入一个新节点的过程为，假设待插入节点的关键字值为key，为了将其插入到表中，先要将它放入二叉排序树中进行查找，若查找成功，则按二叉查找树的定义，待插入节点已经存在，不必插入；否则，将新节点插入到表中。因此，新插入的节点一定是作为叶子节点添加到表中去的。其相关示例代码如下：

    相关代码：

    /**
 * 用于往二叉树中插入一个新的节点
 * @param key 该节点的关键字
 * @param data 该节点的相关数据
 * @return 插入的结果，返回false有两种情况，一种是节点本身已存在，一种是需要插入的节点的关键字值为null
 */
public boolean insert(Comparable key,Object data)
{
	if(key==null)
		return false;
	if(root==null)
	{
		root=new BinarySearchTreeNode(key,data);
		return true;
	}
	else
		return insertNode(root,key,data);
}
/**
 * 往二叉查找树中插入相关的节点
 * @param key 节点的关键字值
 * @param data 节点的相关数据
 * @param node 需要进行插入的子树的根节点
 * @return 插入的结果
 */
public boolean insertNode(BinarySearchTreeNode node,Comparable key,Object data)
{
	int compare=key.compareTo(node.key);
	//已存在节点时，返回false
	if(compare==0)
		return false;
	//要进行插入的节点比根节点的关键字值小的时候
	else if(compare<0)
	{
		//左子树为空则插入左子树
		if(node.left==null)
		{
			node.left=new BinarySearchTreeNode(key,data);
			return true;
		}
		//非空则继续递归的查找
		else
			return insertNode(node.left,key,data);
	}
	else
	{
		if(node.right==null)
		{
			node.right=new BinarySearchTreeNode(key,data);
			return true;
		}
		else
			return insertNode(node.right,key,data);
	}
}

    二叉树的删除操作：

     与在二叉树上进行插入操作的要求相同，从二叉查找树中删除一个节点，要保证删除后仍然是一棵二叉查找树。根据二叉查找树的结构特征，删除操作可分为4种情况来考虑：

    1. 若待删除的节点是叶子节点，则直接删除该节点即可。若该节点同时也是根节点，则删除后二叉查找树变为空树

    2. 若待删除的节点只有左子树，没有右子树，则根据二叉排序树的特点，可以直接将其左子树的根节点替代被删除节点的位置，即若被删除的节点为其双亲节点的左孩子，则将被删除节点的唯一左孩子收为其双亲节点的左孩子；否则收其为双亲节点的右孩子

    3. 待删除的节点只有右子树，而无左子树。则可以直接将其右子树的根节点替代被删除节点的位置，即若被删除的节点为其双亲节点的左孩子，则将被删除节点的唯一右孩子收其为双亲节点的左孩子；否则收为其双亲节点的右孩子

    4. 待删除节点既有左子树，又有右子树。根据二叉查找树的特点，可以用被删除节点的中序遍历序列下的前驱节点(或者中序遍历序列下的后继节点)替代被删除节点，同时删除其中序遍历序列下的前驱节点(或中序遍历序列下的后继节点)。而被删除节点(指的是新的删除节点)在中序遍历下的前驱无右子树(被删除节点在中序遍历下的无后继左子树)因而问题转化为情况2或者情况3

    以下代码中，当其删除节点的左右子树均存在的时候，考虑的是选择其中序遍历序列下的后继节点替代被删除节点

    相关代码：

    /**
 * 用于删除操作
 * @param key 删除的节点的关键字
 * @return 返回所删除节点所对应的数据，当不存在关键字时返回null
 */
public Object delete(Comparable key)
{
	if(key==null)
		return null;
	else
		return remove(root,key,null);
}

/**
 * 用于删除操作所调用的一个方法，在以node为根的二叉查找树中删除关键字值为key的节点，parent为node的父节点，采用递归的方式
 * @param node 以此节点为根的二叉树
 * @param key 需要进行删除节点的关键字
 * @param parent 以node节点为根的二叉树的node节点的父节点
 * @return 所删除节点的数据
 */
public Object remove(BinarySearchTreeNode node,Comparable key,BinarySearchTreeNode parent)
{
	if(node!=null)
	{
		int compare =key.compareTo(node.key);
		//从左子树中进行删除
		if(compare<0)
		{
			return remove(node.left,key,node);
		}
		//从右子树中进行删除
		else if(compare>0)
		{
			return remove(node.right,key,node);
		}
		//当前节点即为要进行删除的节点
		else
		{
			//当前要进行删除的节点的数据
			Object result=node.data;
			//当前要进行删除的节点的左右子树均存在
			if(node.left!=null&&node.right!=null)
			{
				//寻找要进行删除节点的替换节点
				BinarySearchTreeNode innext=node.right;
				//进行进行替换的节点的父节点
				BinarySearchTreeNode innextParent=node;
				//寻找右子树下的最左孩子节点
				while(innext.left!=null)
				{
					innextParent=innext;
					innext=innext.left;
				}
				//改变删除节点的相关数据
				node.data=innext.data;
				node.key=innext.key;
				//递归的从二叉查找树中删除要进行替换的节点
				remove(node.right,innext.key,node);
			}
			//以下考虑的情况均当前删除节点缺少左子树或者右子树的情况
			else
			{
				//当前要进行删除的节点不为根节点的时候
				if(parent!=null)
				{
					//当左子树不为空的时候
					if(node.left!=null&&node.right==null)
					{
						//当前节点为其左子树节点的时候
						if(node==parent.left)
						{
							parent.left=node.left;
						}
						//当前节点为其右子树节点的时候
						else
						{
							parent.right=node.left;
						}
					}
					//当右子树不为空的时候
					else if(node.left==null&&node.right!=null)
					{
						//当前节点为其左子树节点的时候
						if(node==parent.left)
						{
							parent.left=node.right;
						}
						//当前节点为其右子树节点的时候
						else
						{
							parent.right=node.right;
						}
					}
				}
				//当前删除的节点为根节点的时候
				else
				{
					if(node.left!=null)
						root=node.left;
					else
						root=node.right;
				}
			}
			//返回其进行删除的节点的值
			return result;
		}
	}
	return null;
}

    其完整代码如下：

    package all_in_tree;
/**
 * 该类用于演示二叉查找树相关的操作
 * @author 学徒
 *
 */
public class BinarySearchTree
{
	//用于指向一棵二叉查找树的根节点的指针
	private BinarySearchTreeNode root;
	
	/**
	 * 二叉查找树的查找操作
	 * @param data 需要进行查找的相关数据
	 * @return 查找到的相关的结果，当查找失败时，返回null
	 */
	public Object search(Comparable key)
	{
		if(key==null)
		{
			return null;
		}
		return toSearch(root,key);
	}
	/**
	 * 在二叉查找树中进行递归的查找的方法
	 * @param data 需要进行查找的数据
	 * @param node 二叉树中某个子树的根节点
	 * @return 查找的节点类的结果
	 */
	private Object toSearch(BinarySearchTreeNode node,Comparable key)
	{
		if(node==null)
		{
			return null;
		}
		//与根节点的相关值进行比较并选择合适的分支
		int compara=node.key.compareTo(key);
		if(compara==0)
			return node.data;
		else if(compara<0)
			return toSearch(node.right,key);
		else
			return toSearch(node.left,key);
	}
	
	/**
	 * 用于往二叉树中插入一个新的节点
	 * @param key 该节点的关键字
	 * @param data 该节点的相关数据
	 * @return 插入的结果，返回false有两种情况，一种是节点本身已存在，一种是需要插入的节点的关键字值为null
	 */
	public boolean insert(Comparable key,Object data)
	{
		if(key==null)
			return false;
		if(root==null)
		{
			root=new BinarySearchTreeNode(key,data);
			return true;
		}
		else
			return insertNode(root,key,data);
	}
	/**
	 * 往二叉查找树中插入相关的节点
	 * @param key 节点的关键字值
	 * @param data 节点的相关数据
	 * @param node 需要进行插入的子树的根节点
	 * @return 插入的结果
	 */
	public boolean insertNode(BinarySearchTreeNode node,Comparable key,Object data)
	{
		int compare=key.compareTo(node.key);
		//已存在节点时，返回false
		if(compare==0)
			return false;
		//要进行插入的节点比根节点的关键字值小的时候
		else if(compare<0)
		{
			//左子树为空则插入左子树
			if(node.left==null)
			{
				node.left=new BinarySearchTreeNode(key,data);
				return true;
			}
			//非空则继续递归的查找
			else
				return insertNode(node.left,key,data);
		}
		else
		{
			if(node.right==null)
			{
				node.right=new BinarySearchTreeNode(key,data);
				return true;
			}
			else
				return insertNode(node.right,key,data);
		}
	}
	
	/**
	 * 用于删除操作
	 * @param key 删除的节点的关键字
	 * @return 返回所删除节点所对应的数据，当不存在关键字时返回null
	 */
	public Object delete(Comparable key)
	{
		if(key==null)
			return null;
		else
			return remove(root,key,null);
	}
	
	/**
	 * 用于删除操作所调用的一个方法，在以node为根的二叉查找树中删除关键字值为key的节点，parent为node的父节点，采用递归的方式
	 * @param node 以此节点为根的二叉树
	 * @param key 需要进行删除节点的关键字
	 * @param parent 以node节点为根的二叉树的node节点的父节点
	 * @return 所删除节点的数据
	 */
	public Object remove(BinarySearchTreeNode node,Comparable key,BinarySearchTreeNode parent)
	{
		if(node!=null)
		{
			int compare =key.compareTo(node.key);
			//从左子树中进行删除
			if(compare<0)
			{
				return remove(node.left,key,node);
			}
			//从右子树中进行删除
			else if(compare>0)
			{
				return remove(node.right,key,node);
			}
			//当前节点即为要进行删除的节点
			else
			{
				//当前要进行删除的节点的数据
				Object result=node.data;
				//当前要进行删除的节点的左右子树均存在
				if(node.left!=null&&node.right!=null)
				{
					//寻找要进行删除节点的替换节点
					BinarySearchTreeNode innext=node.right;
					//进行进行替换的节点的父节点
					BinarySearchTreeNode innextParent=node;
					//寻找右子树下的最左孩子节点
					while(innext.left!=null)
					{
						innextParent=innext;
						innext=innext.left;
					}
					//从二叉查找树中删除该要进行替换的节点即节点innext
					innextParent.left=null;
					//改变删除节点的相关数据
					node.data=innext.data;
					node.key=innext.key;
				}
				//以下考虑的情况均当前删除节点缺少左子树或者右子树的情况
				else
				{
					//当前要进行删除的节点不为根节点的时候
					if(parent!=null)
					{
						//当左子树不为空的时候
						if(node.left!=null&&node.right==null)
						{
							//当前节点为其左子树节点的时候
							if(node==parent.left)
							{
								parent.left=node.left;
							}
							//当前节点为其右子树节点的时候
							else
							{
								parent.right=node.left;
							}
						}
						//当右子树不为空或者删除节点为叶子节点的时候
						else 
						{
							//当前节点为其左子树节点的时候
							if(node==parent.left)
							{
								parent.left=node.right;
							}
							//当前节点为其右子树节点的时候
							else
							{
								parent.right=node.right;
							}
						}
					}
					//当前删除的节点为根节点的时候
					else
					{
						if(node.left!=null)
							root=node.left;
						else
							root=node.right;
					}
				}
				//返回其进行删除的节点的值
				return result;
			}
		}
		return null;
	}
}

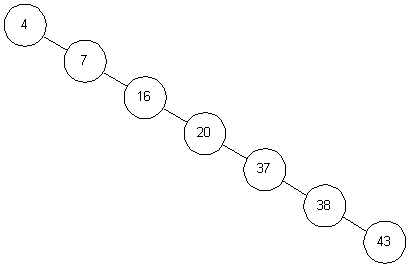
    分析：对于二叉查找树，其树结构是在插入和删除节点中动态进行生成的，为此，其查找树的深度依赖于插入节点的顺序。为此，其可能出现如下图所示的一种情况。当插入节点的顺序为有序的时候(节点关键字为有序的)其可能会出现严重“偏拐”的现象而导致其插入和删除的效率均变为O（n）。而平衡二叉树的提出便是为了解决这个问题。详情请点击查看相关博文K：平衡二叉树(AVL)

    二叉查找树的最坏情况示意图

    回到目录|·(工)·）
  • 相关阅读:
    【转】忘记密码功能的安全实现(邮件方式)
    windows7下安装gem包---bcrypt-ruby
    Ruby中的%表示法
    ruby中特殊的全局变量
    rails中一个窗体多个模型——fields_for
    【转】深刻理解render 和 redirect_to
    UML核心元素--分析类
    UML核心元素--包
    UML核心元素--边界
    UML核心元素--用例
  • 原文地址：https://www.cnblogs.com/MyStringIsNotNull/p/8296343.html
Copyright © 2020-2023  润新知