快速莫比乌斯变换（FMT）

快速莫比乌斯变换（FMT）

原文出处：虞大的博客。此仅作蒟蒻本人复习用~

给定两个长度为n的序列 (a_0, a_1, cdots, a_{n-1})和(b_0, b_1, cdots, b_{n-1})，你需要求出一个序列(c_0, c_1, cdots, c_{n-1})，其中(c_k)满足：(c_k = sumlimits_{i mid j = k} a_i b_j)。其中|表示按位或。(n leq 10^6)表示序列长度。

显然发现(i∣j=k)这个条件不怎么好处理，如果我们作一个集合的 "前缀和" ，即令(P_i = sumlimits_{j subseteq i} p_j)（(i&j=j)），那么有：(C_k = sum_{k_0 subseteq k} c_i = sum_{k_0 subseteq k} sum_{i cup j = k_0} a_i b_j = sum_{i cup j subseteq k} a_i b_j = left( sum_{i subseteq k} a_i ight) left( sum_{j subseteq k} b_j ight) = A_k cdot B_k)

所以说我们就把集合并卷积转化成了两个“前缀和”集合的(O(n))运算，和FFT差不多。现在的问题就是怎么快速算出这些“前缀和”集合。

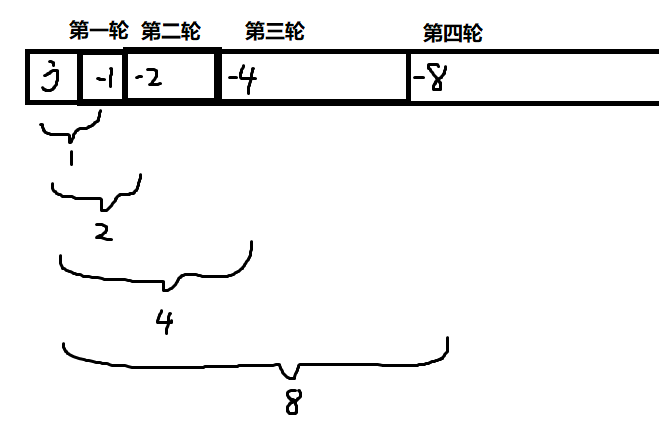
我们可以画一张图，图中每一行代表一个(P_i)。这一行有哪些格子涂蓝，就代表它是哪些(p_i)的和：

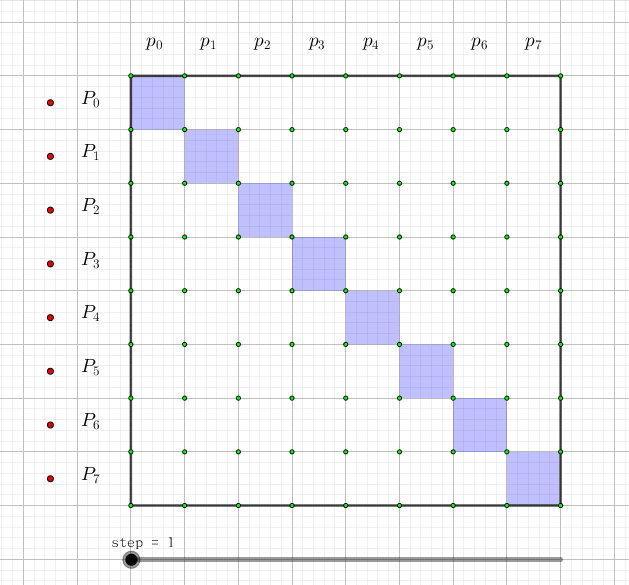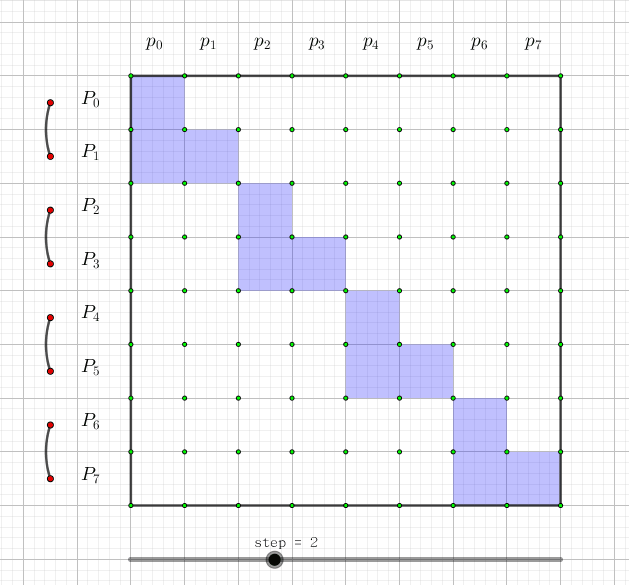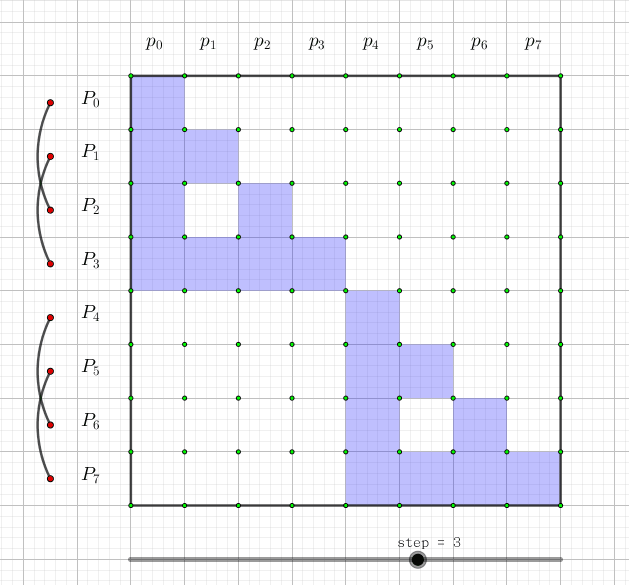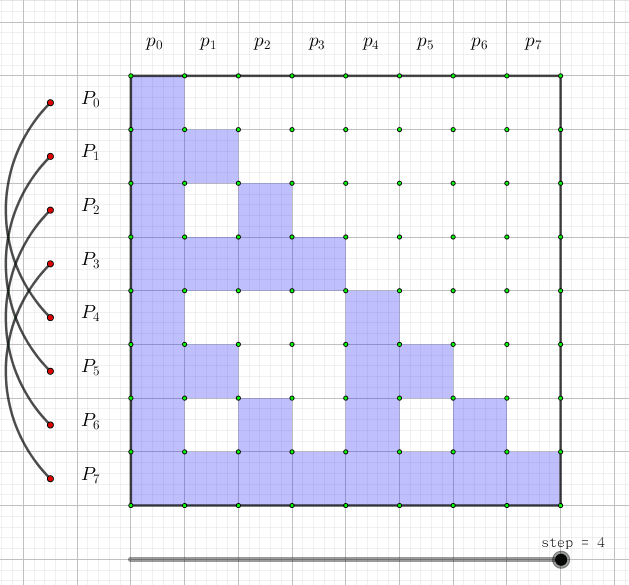
如果用动态规划来理解的话，令(f[i][j])表示j的开头(2^i)个数中为权值为1的数的和， 那么转移显然就是(f[i+1][j+2^i]+=f[i][j])(j的(2^i)位是0)。其中j这一维是可以压掉的。

如果改变一下你脑海中的求和顺序，那么循环内的一次加法，就相当于一个集合的前面2^i个元素的值被加上了。

如果要把(f)还原该怎么办呢？只要把+=改成-=就行了~（不会证，但是真的很好记）

#include <cctype>
#include <cstdio>
using namespace std;

typedef long long LL;
const LL maxn=2e6+5;
LL n, l, bits, a[maxn], b[maxn], c[maxn];

void FMT(LL *f, LL flag){
	for (LL i=0; i<bits; ++i)
		for (LL j=0; j<l; ++j)
			if ((j>>i&1)==0) f[j|1<<i]+=(~flag?f[j]:-f[j]);
}

inline void getint(LL &x){
	char ch; x=0;
	for (; ch=getchar(), !isdigit(ch););
	for (x=ch-48; ch=getchar(), isdigit(ch);)
		x=(x<<3)+(x<<1)+ch-48;
}

int main(){
	getint(n); l=1;
	while (l<n) l<<=1, ++bits;
	for (LL i=0; i<n; ++i) getint(a[i]); FMT(a, 1);
	for (LL i=0; i<n; ++i) getint(b[i]); FMT(b, 1);
	for (LL i=0; i<l; ++i) c[i]=a[i]*b[i]; FMT(c, -1);  
	//坑点1：乘法可能爆LL 坑点二：i要到l 
	for (LL i=0; i<n; ++i) printf("%lld ", c[i]);
	return 0;
}