树链剖分
马上就省选了,是时候好好的再把以前遗失的知识点,拾回来一点了。
什么是树链剖分
树链剖分是一种对树形结构的划分算法,它可以将一棵树通过轻重链的不同划分为最多 logn 条链,并且一个点有且只会出现在一条链中,然后再通过某些神奇的数据结构来维护每条链,来维护树上的某些与树链有关的信息
链上的极值,树链的异或和
类似与树上倍增
跳树链的时候需要树上倍增的思想所以这是前置知识。
树链剖分有什么用
如果你学过树上倍增并且了解过树链剖分的话,树链剖分与树上倍增之间的关系就非常明显了。
树上倍增能做的,树链剖分都能做某些冷门骚操作除外;但树链剖分能做的,树上倍增只能做一部分。
首先我们先来看树上倍增,我们在做树上倍增的时候,是可以维护区间极值或和的,但是当我们有了树上的权值修改,当场暴毙
这时候我们就需要用到树链剖分了。
引入概念
轻儿子 || 链 && 重儿子 || 链
对于一个树上的非叶子节点,它的所有儿子中子树大小最大的儿子为重儿子,其余的都是轻儿子。从他连向重儿子的边叫做重链,其余的边叫做轻链。
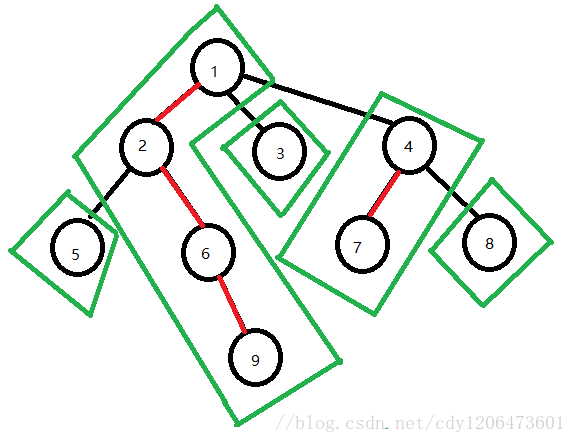
盗一张图,举个例子理解
图中一共有5条重链,分别是:
- 1 -> 2 -> 6 -> 3
- 5
- 3
- 4 -> 7
- 8
然后我们就可以把一棵树划分成如图这样
我们需要维护什么
- 结构体tr[],维护整棵树的信息
- tr[x].dep,维护x节点的深度
- tr[x].top,维护x节点
- tr[x].fa,维护x节点的父亲
- tr[x].v,维护x节点的权值
- tr[i].id,维护x的dfs序
- tr[i].son,维护x的重儿子
- tr[i].siz,维护x的子树大小
- to[i],维护dfs序为i的节点
如何维护
很明显我们在一棵树上可以通过dfs来完成信息的收集
那么我们就来进行dfs
第一次dfs
维护siz,dep,fa,son;
直接上代码吧,都看得懂
void dfs1(int x,int dep) {
tr[x].d=dep;tr[x].siz=1;//初始化
int maxn=0;
for(int i=link[x];i;i=e[i].next) {//邻接表存树
int v=e[i].y;
if(v==tr[x].fa) continue;//如果是父亲
tr[v].fa=x;//不是父亲就是儿子
dfs1(v,dep+1);//向下递归先更新儿子再更新父亲
tr[x].siz+=tr[v].siz;//更新siz
if(maxn<tr[v].siz) maxn=tr[v].siz,tr[x].son=v;//更新重儿子
}
}
第二次dfs
更新top,to,id;
每次优先dfs重儿子来保证重链分在一起以及重儿子的dfs序连续
void dfs2(int x,int k) {
tr[x].top=k;tr[x].id=++num;//更新top和dfs序
wt[num]=w[x];
if(tr[x].son) dfs2(tr[x].son,k);//重儿子的top为父亲的top
for(int i=link[x];i;i=a[i].next) {
int v=a[i].y;
if(v==tr[x].fa||v==tr[x].son) continue;
dfs2(v,v);//轻儿子top为自己
}
}
基本操作
单间修改
直接按dfs序编号对应修改
路径修改
我们默认用线段树维护各个链
分为以下情况
x,y在同一个链上
直接线段树区间修改
x,y不在同一个链上
我们想办法将其向同一个链上靠拢
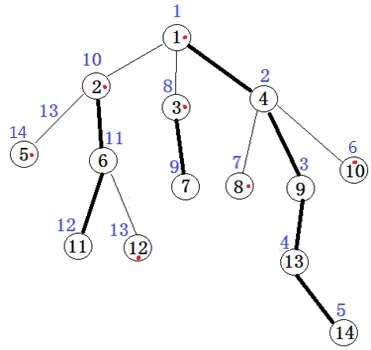
我们观察上面这幅图
因为一个从x到y的路径一定是从x到lca(x,y),再从lca(x,y)到y
所以我们可以将路径分成两条
其中我们可以对lca的位置分情况讨论
如果lca与x或y在同一个链上
我们只需要对于另一个点对应的链向上跳树链
然后对于经过的树链做线段树的区间修改就好了
如果lca不在x或y的任何一个链上
那么我们参照倍增的方法
每次比较tr[x].top与tr[y].top的深度
将较深的点向上跳到tr[tr[x].top].fa所在的链
由于是在一棵树上跳转所以最后一定会跳到同一条链上那么我们只需要对于所有经过的链进行区间修改即可
inline int ask(int x,int y) {//路径查询
int ans=0;
while(tr[x].top!=tr[y].top) {
if(tr[tr[x].top].d<tr[tr[y].top].d) swap(x,y);
int res=query(1,1,n,tr[tr[x].top].id,tr[x].id);
ans=(ans+res)%mod;
x=tr[tr[x].top].fa;
}
if(tr[x].d>tr[y].d) swap(x,y);
int res=query(1,1,n,tr[x].id,tr[y].id);
ans+=res;
return ans%mod;
}
inline int ask2(int x) {//子树查询
return query(1,1,n,tr[x].id,tr[x].id+tr[x].siz-1);
}
询问
和修改操作相似
对于单点的查询直接查就好
对于路径的查询先找到所有有用的链,然后只需要对于这些链做对应的线段树查询即可
inline void change(int x,int y,int k) {//路径修改
while(tr[x].top!=tr[y].top) {
if(tr[tr[x].top].d<tr[tr[y].top].d) swap(x,y);
update(1,1,n,tr[tr[x].top].id,tr[x].id,k);
x=tr[tr[x].top].fa;
}
if(tr[x].d>tr[y].d) swap(x,y);
update(1,1,n,tr[x].id,tr[y].id,k);
}
inline void change2(int x,int k) {//子树修改
update(1,1,n,tr[x].id,tr[x].id+tr[x].siz-1,k);
}
时间复杂度
由于只会将树最多剖分成log n个链,并且要用线段树维护区间操作
所以整体的复杂度是(O(nlog^2n)),但在实际应用中肯定达不到这个上界所以一般可以用来写(10^5)左右的数据
例题
P3384 【模板】树链剖分
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
样例
输入
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
输出
2
21
说明
时空限制:1s,128M
数据规模:
对于100%的数据:(, N leq {10}^5,M leq {10}^5)
( 其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233 )
样例说明:
树的结构如下:

各个操作如下:

故输出应依次为2、21(重要的事情说三遍:记得取模)
题解
就是最基本的树链操作套模板就好
#include<bits/stdc++.h>
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc(){return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;}
inline int read() {
int n=1,num=0; char ch=getchar();
while(!isdigit(ch)) {n=(ch=='-')?-1:1;ch=getchar();}
while(isdigit(ch)) {num=(num<<1)+(num<<3)+(ch^48);ch=getchar();}
return n*num;
}
int n,m,rt,mod,num,tot,w[100010],link[100010],wt[100010];
int a[500010],laz[500010];
struct gg {
int d,siz,fa,son,id,top,v;
}tr[100010];
struct edge {
int y,next;
}e[200010];
inline void init(int xx,int yy) {
e[++tot].y=yy;e[tot].next=link[xx];link[xx]=tot;
}
inline void pushdown(int rt,int lenn){
laz[rt<<1]+=laz[rt];
laz[rt<<1|1]+=laz[rt];
a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
a[rt<<1|1]+=laz[rt]*(lenn>>1);
a[rt<<1]%=mod;
a[rt<<1|1]%=mod;
laz[rt]=0;
}
inline void build(int x,int l,int r){
if(l==r){
a[x]=wt[l]%mod;return;
}
int mid=l+r>>1;
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
a[x]=(a[x<<1]+a[x<<1|1])%mod;
}
inline int query(int x,int l,int r,int L,int R){
int ans=0;
if(L<=l&&r<=R){return a[x]%mod;}
else {
int len=r-l+1,mid=l+r>>1;
if(laz[x])pushdown(x,len);
if(L<=mid) ans=(ans+query(x<<1,l,mid,L,R))%mod;
if(R>mid) ans=(ans+query(x<<1|1,mid+1,r,L,R))%mod;
}
return ans;
}
inline void update(int x,int l,int r,int L,int R,int k){
int len=r-l+1;
if(L<=l&&r<=R){
laz[x]+=k;
a[x]+=k*len;
}
else{
int mid=l+r>>1;
if(laz[x])pushdown(x,len);
if(L<=mid)update(x<<1,l,mid,L,R,k);
if(R>mid)update(x<<1|1,mid+1,r,L,R,k);
a[x]=(a[x<<1]+a[x<<1|1])%mod;
}
}
void dfs1(int x,int dep) {
tr[x].d=dep;tr[x].siz=1;//初始化
int maxn=0;
for(int i=link[x];i;i=e[i].next) {//邻接表存树
int v=e[i].y;
if(v==tr[x].fa) continue;//如果是父亲
tr[v].fa=x;//不是父亲就是儿子
dfs1(v,dep+1);//向下递归先更新儿子再更新父亲
tr[x].siz+=tr[v].siz;//更新siz
if(maxn<tr[v].siz) maxn=tr[v].siz,tr[x].son=v;//更新重儿子
}
}
void dfs2(int x,int k) {
tr[x].top=k;tr[x].id=++num;//更新top和dfs序
wt[num]=w[x];
if(tr[x].son) dfs2(tr[x].son,k);
for(int i=link[x];i;i=e[i].next) {
int v=e[i].y;
if(v==tr[x].fa||v==tr[x].son) continue;
dfs2(v,v);
}
}
inline int ask(int x,int y) {//路径查询
int ans=0;
while(tr[x].top!=tr[y].top) {
if(tr[tr[x].top].d<tr[tr[y].top].d) swap(x,y);
int res=query(1,1,n,tr[tr[x].top].id,tr[x].id);
ans=(ans+res)%mod;
x=tr[tr[x].top].fa;
}
if(tr[x].d>tr[y].d) swap(x,y);
int res=query(1,1,n,tr[x].id,tr[y].id);
ans+=res;
return ans%mod;
}
inline int ask2(int x) {//子树查询
return query(1,1,n,tr[x].id,tr[x].id+tr[x].siz-1);
}
inline void change(int x,int y,int k) {//路径修改
while(tr[x].top!=tr[y].top) {
if(tr[tr[x].top].d<tr[tr[y].top].d) swap(x,y);
update(1,1,n,tr[tr[x].top].id,tr[x].id,k);
x=tr[tr[x].top].fa;
}
if(tr[x].d>tr[y].d) swap(x,y);
update(1,1,n,tr[x].id,tr[y].id,k);
}
inline void change2(int x,int k) {//子树修改
update(1,1,n,tr[x].id,tr[x].id+tr[x].siz-1,k);
}
int main() {
n=read();m=read();rt=read();mod=read();
for(int i=1;i<=n;++i) tr[i].v=w[i]=read();
for(int i=1;i<n;++i) {
int x=read(),y=read();
init(x,y);init(y,x);
}
tr[rt].fa=rt;tr[rt].top=rt;
dfs1(rt,1);dfs2(rt,rt);build(1,1,n);
while(m--) {
int t,x,y,z;
t=read();
if(t==1) {
x=read(),y=read(),z=read();
change(x,y,z);
}
else if(t==2) {
x=read();y=read();
cout<<ask(x,y)<<endl;
}
else if(t==3) {
x=read();z=read();
change2(x,z);
}
else {
x=read();
cout<<ask2(x)<<endl;
}
}
return 0;
}
好长啊!!!