[NOI2007]社交网络

题目：洛谷P2047、BZOJ1491、vijos P1591、codevs1796。

题目大意：给你一张带权无向图。令$C_{s,t}$表示从s到t的不同的最短路的数目，$C_{s,t}(v)$表示经过v从s到t的不同的最短路的数目。则定义：

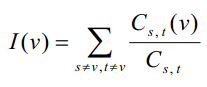
为节点v的重要程度。问每个节点的重要程度（保留3位小数）。

解题思路：用floyd求出每个节点的最短路时，可以顺便统计出两点见最短路的数量。

设$num_{i,j}$表示i到j的最短路的数量(即$C_{i,j}$)，$dis_{i,j}$表示i到j的最短路长度，则

$num_{i,j}=num_{i,k}*num_{k,j}$(当$dis_{i,j}>dis_{i,k}+dis_{k,j}$时)

$num_{i,j}=num_{i,j}+num_{i,k}*num_{k,j}$(当$dis_{i,j}=dis_{i,k}+dis_{k,j}$时)

初始时，对于每两个有边直接相连的点i和j，$num_{i,j}=1$。

然后我们发现，若s为起点t为终点，则经过v的最短路条数为s到v的最短路条数乘v到t的最短路条数，即$C_{s,t}(v)=C_{s,v}*C_{v,t}$。

那么枚举起点和终点，代入式子计算即可。

时间复杂度$O(n^3)$。

C++ Code：

#include<cstdio>
#include<cstring>
#define ll long long
#define N 105
int n,m;
ll dp[N][N],num[N][N];
int main(){
	scanf("%d%d",&n,&m);
	memset(dp,0x3f,sizeof dp);
	memset(num,0,sizeof num);
	while(m--){
		int u,v,t;
		scanf("%d%d%d",&u,&v,&t);
		dp[u][v]=dp[v][u]=t;
		num[u][v]=num[v][u]=1;
	}
	for(int i=1;i<=n;++i)dp[i][i]=0;
	for(int k=1;k<=n;++k)
	for(int i=1;i<=n;++i)
	if(i!=k)
	for(int j=1;j<=n;++j)
	if(i!=j&&j!=k){
		if(dp[i][j]>dp[i][k]+dp[k][j]){
			dp[i][j]=dp[i][k]+dp[k][j];
			num[i][j]=num[i][k]*num[k][j];
		}else 
		if(dp[i][j]==dp[i][k]+dp[k][j])num[i][j]+=num[i][k]*num[k][j];
	}
	double ans;
	for(int k=1;k<=n;++k){
		ans=0.0f;
		for(int i=1;i<=n;++i)
		if(i!=k)
		for(int j=1;j<=n;++j)
		if(i!=j&&j!=k){
			if(dp[i][j]==dp[i][k]+dp[k][j])
			ans+=(double)(num[i][k]*num[k][j])/num[i][j];
		}
		printf("%.3f
",ans);
	}
	return 0;
}