题目:洛谷P2144、BZOJ1002、codevs2886。
题目大意:给你n+1($nle 100$)个节点,除第一个节点外的所有节点围绕第一个节点排列成环装。中间的节点和所有节点都能连边,环上相邻两个节点也能连边。问该图生成树的数量(即有多少种不同方法能用n条边连接所有节点)。
以下是n=3时的16种方案。
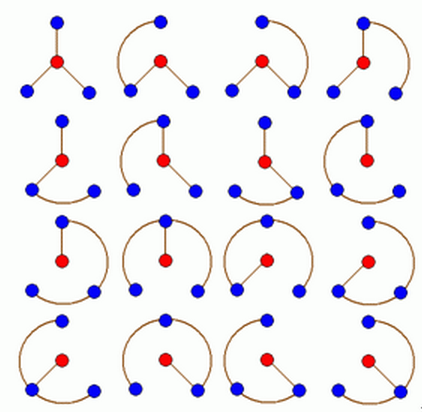
解题思路:此题n小于等于100,但是无法迅速找到能求出解的方法。
此类题目通常都有规律。
我们发现,当n=1、2、3、4、5时,答案分别为1、5、16、45、121,即$1^2$,$3^2-4$,$4^2$,$7^2-4$,$11^2$。
不考虑减4的情况,观察底数,是不是斐波那契数列的形态?
那么我们递推出该斐波那契数列,然后求出第n项的平方。
然后发现,n为偶数时需要减去4,那么减去4即可。
这就是此题的规律。
结果非常大,要用高精度。
C++ Code:
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
struct bg{
ll a[700];
int len;
}f[101];
void add(ll a[],int lena,ll b[],int lenb,ll c[],int& lenc){
lenc=lena;
if(lenc<lenb)lenc=lenb;
for(int i=1;i<=lenc;++i){
c[i]+=a[i]+b[i];
c[i+1]+=c[i]/100000000;
c[i]%=100000000;
}
while(c[lenc+1])++lenc;
}
void sqr$print(ll a[],int lena,int odd){
ll b[700]={0};
int lenb=(lena<<1)-1;
for(int i=1;i<=lena;++i)
for(int j=1;j<=lena;++j){
b[i+j-1]+=a[i]*a[j];
b[i+j]+=b[i+j-1]/100000000;
b[i+j-1]%=100000000;
}
while(b[lenb+1])++lenb;
while(!b[lenb])--lenb;
if(!odd){
int now=1;
b[1]-=4;
while(b[now]<0){
b[now]+=100000000;
--b[now++];
}
}
while(b[lenb+1])++lenb;
while(!b[lenb])--lenb;
printf("%d",(int)b[lenb]);
for(int i=lenb-1;i;--i)printf("%08d",(int)b[i]);
putchar('
');
}
int main(){
memset(f,0,sizeof f);
int n;
scanf("%d",&n);
f[1].a[1]=f[1].len=f[2].len=1;
f[2].a[1]=3;
for(int i=3;i<=n;++i)
add(f[i-2].a,f[i-2].len,f[i-1].a,f[i-1].len,f[i].a,f[i].len);
sqr$print(f[n].a,f[n].len,n&1);
return 0;
}