Manacher算法,是由一个叫Manacher的人在1975年发明的,可以在$O(n)$的时间复杂度里求出一个字符串中的最长回文子串。
例如这两个回文串“level”、“noon”,Manacher算法先对其进行一个处理:
level --> #l#e#v#e#l#
noon --> #n#o#o#n#
这样的好处就是,不论回文子串的长度是奇是偶,最后求出的回文子串长度都是奇数的,就不用分类讨论了。
我们用p[i]表示以i为中心的最长回文子串向两边扩展的长度,例如:
s # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
p 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
我们发现,p[i]-1刚好为原串以i位置为中心的最长回文子串长度。
在Manacher算法中,需要两个辅助变量。id为当前最长回文子串的中心,mx为以id为中心的最长回文子串的右边界(id+p[id])。这个算法的核心部分在这里:
if(mx>i)p[i]=min(p[(id<<1)-i],mx-i);else p[i]=1;
当 mx - i > p[j] 的时候,以s[j]为中心的回文子串包含在以s[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 p[i] = p[j]。
当 p[j] > mx - i 的时候,以s[j]为中心的回文子串不完全包含于以s[id]为中心的回文子串中,但是由于对称性,以s[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 p[i] >= mx - i。至于mx之后的部分是否对称,就只能一个一个匹配了。
当 mx < i 的时候,我们就无法对 p[i] 进行更多的推算,只能一个一个匹配。
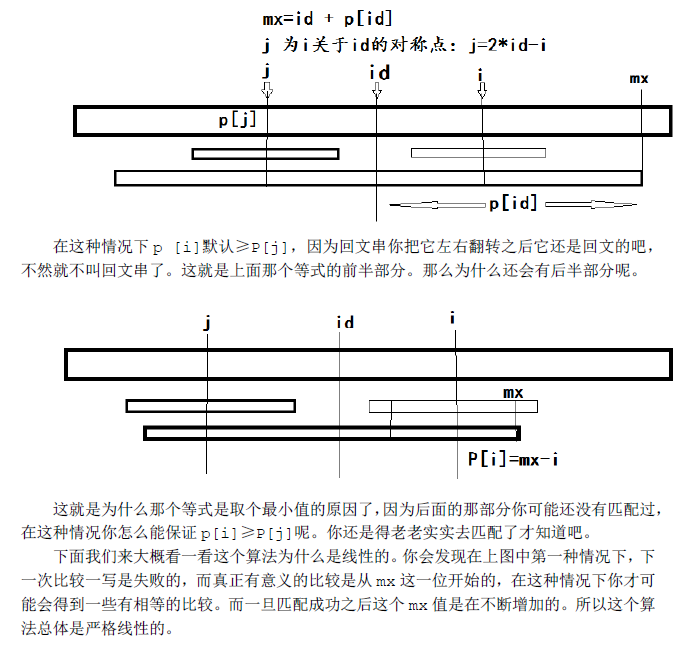
上图给出了Manacher的详解和线性复杂度的证明。
以下是核心代码:
C++ Code:
void manacher(){
int mx=0,id=0;
for(i=1;i<=n;++i){
if(mx>i)p[i]=min(p[(id<<1)-i],mx-i);else p[i]=1;
while(s[i-p[i]]==s[i+p[i]])++p[i];
if(i+p[i]>mx)mx=i+p[id=i];
}
}