110.Balanced Binary Tree
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
很早以前做的了 准备把这些笔记都转移到博客园上 其一加深理解 其二再打一遍也有好处
这题大意 给出一个二叉树 判断这个二叉树 是否平衡 平衡的条件为 任意一个节点的左子树和右子树高度相差不超过一
思路很简单 首先要有一个得出树高度的函数
节点为空 树高度为零 否则树的高度为左子树的高度和右子树的高度中最大的那个加一,加一的意思就是加上自身这个节点的高度
判断左子树和右子树高度是否相差大于一 如果大于一 返回一个标记数 可以用-1标记
直接码代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public boolean isBalanced(TreeNode root) {
return height(root)!=-1;
}
public int height(TreeNode root){
if(root==null)
return 0;
int left=height(root.left);
int right=height(root.right);
if(left==-1||right==-1||Math.abs(left-right)>1)
return -1;
return Math.max(left,right)+1;
}
}
一次过了

看看 detail
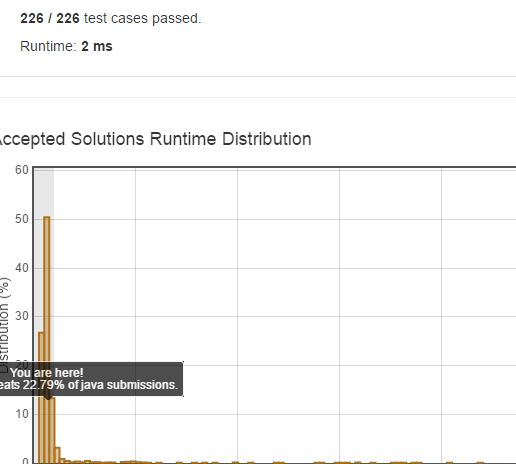
2ms 感觉有点长了 我觉得应该是0ms级别的
惯例 学习别人的优秀解法 看看discuss 里最受欢迎的那个
public class Solution {
public boolean isBalanced(TreeNode root) {
if(null == root) {
return true;
}
return Math.abs(height(root.left) - height(root.right)) < 2 && isBalanced(root.left) && isBalanced(root.right);
}
public int height(TreeNode root) {
if(null == root) {
return 0;
}
return 1 + Math.max(height(root.left), height(root.right));
}
}
恩 其实和我的思路一样 只是写法不同 ~