排序算法之快速排序

思路：快速排序也是利用了分治算法。总体是，首先在将要比较的数组中找到一个基准，然后用该基准和数组中的剩余元素进行比较，小于该基准的就放到该基准的左侧，大于该基准的就放到右侧，紧接着再对左右两侧的数组再进行快速排序，依次逐渐递归，最后生成的数组就是有序数组。

图片引用网址 ：http://www.cnblogs.com/MOBIN/p/4681369.html

　　　　　　

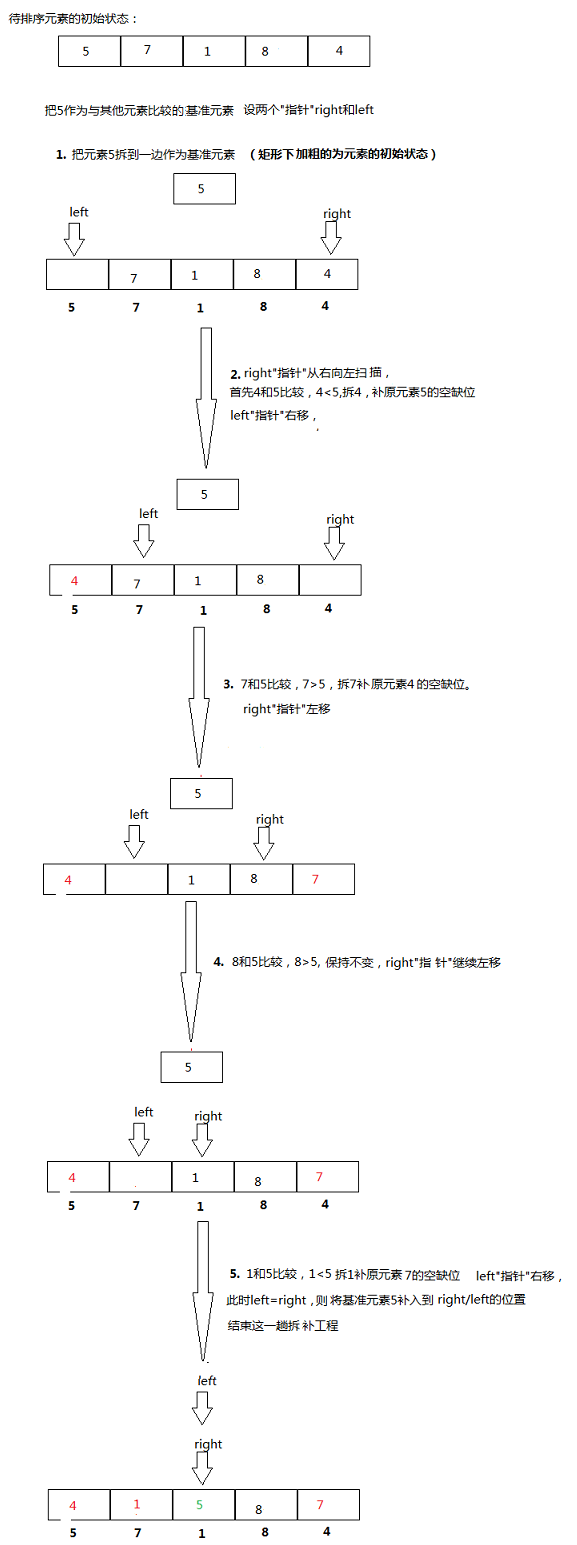
注意：left，right指针，迭代的方向，和它们是否指向可覆盖的索引有关。比如：left指向可以覆盖的索引，那么left就不再继续右移，而是right进行左移。

/*
 * quickSort.cpp
 *
 *  Created on: 2017年6月4日
 *      Author: MrZhang
 */

#include <iostream>
using namespace std;

template <typename T >
int partition( T arr[], int iLeft, int iRight )
{
　　//优化： swap（arr[iLeft],arr[rand()%(iRight - iLeft +　１)+iLeft]）;
    T pivot = arr[iLeft];
    int L = iLeft, R = iRight;  //初始化时，L指向第一个坑。

    while( L < R )
    {
        while( arr[R] >= pivot && R > L )  //首先从右向左迭代，直到在右侧留下一个可以填充的索引
        {
            R--;
        }
        arr[L] = arr[R];//右侧arr[R]可以被覆盖

        while( arr[L] <= pivot && L < R ) //然后从左向右迭代，直到在左侧留下一个可以填充的索引
        {
            L++;
        }
        arr[R] = arr[L]; //左侧arr[L]可以被覆盖
    }
    arr[L] = pivot;
    return L;
}

template < typename T >
void __quickSort( T arr[], int iLeft, int iRight )
{
    if( iLeft >= iRight )
    {
        return;
    }
    int p = partition(arr, iLeft, iRight );
    __quickSort( arr, iLeft, p - 1 );
    __quickSort( arr, p + 1, iRight );
}

template < typename T >
void quickSort( T arr[], int iMaxNum )
{
    __quickSort( arr, 0, iMaxNum -1 );
}

int main( )
{
    //setbuf(stdout,NULL);
    unsigned int pucBuff[10] = {3,4,1,7,3,7,8,9,4,0};
    cout << "排序前
" << endl;
    for( unsigned int i = 0; i < sizeof(pucBuff)/sizeof(int); i++ )
    {
        cout << pucBuff[i] << " " ;
    }
    cout << endl;

    quickSort( pucBuff, sizeof(pucBuff)/4 );
    cout << "排序后
" << endl;
    for( unsigned int i = 0; i < sizeof(pucBuff)/4; i++ )
    {
        cout<< pucBuff[i]<< " ";
    }
    cout<<endl;
    return 1;
}

总结：

　　对于上面代码的快速排序算法，如果给定的数组接近有序，那么该算法时间复杂度接近于O（n2）。

　　优化方法为采用随机的方法选择基准元素。然后和左侧第一元素进行交换，依然选择左侧第一个元素。其他代码不用变化。