其实是寒假复习高数时摸索出来的一些小玩意了,一直想整理一下过程,今天就在这里做些简单的讨论吧。
我们经常可以看到一些模拟水纹特效的图像处理程序,在惊叹其效果的同时想必也曾试图解释它们的实现原理吧。我在网上看过一些相关的讨论或博文,从中也获得了不少的启发。今天呢,就在这篇随笔里简洁介绍下我对水纹渲染算法的思考与实现吧。
在图像上模拟水纹产生的折射,乍一看的确让人有种望而生畏的感觉,毕竟水纹这东西看上去就是繁杂而凌乱的,更何况要去分析每一处的光线折射呢?当然,为使得这个看似复杂的问题得以解决我们首先要对其蕴含的物理学规律有一定的了解。说到水纹就不得不提一下机械波了。水纹就是机械波的一种体现嘛,理所当然服从机械波的性质与规律。其次,说到机械波就又需要谈谈简谐运动了,简谐波是常见的机械波,无论在应用还是科研领域均具有十分重要的地位。还有就是牵扯到整个问题核心的光学折射规律,我们的最终目的就是建立形式化的过程来模拟水纹的折射这一自然现象。
自然界的水纹真是各式各样,让人凌乱到无法入手。好在物理学告诉我们复杂的波在传播过程中服从惠根斯原理,这使得我们可以将问题先界定到最简单的单个简谐波源所产生的激波上来讨论。当然在我们的讨论中如果牵扯到越多的物理特性,那么意味着问题的复杂程度会急剧增加。这里我会提前说明,在下文的讨论中完全忽略机械波的反射、衍射等特性(在我们所讨论的问题中意义不大)。
光线的折射是由于所传递的介质的改变而引起的。在水纹折射中,光线是从水底传上来并竖直向上传递直到显示区(可以理解为只接受平行光的荧光屏),这里需要强调的是我们所模拟的是平行光成像,而非人眼直接观察的那样是透视投影的一种。虽然与直觉相悖,但其实可以近似的看做等效。当光线由水底折射到水面以上,折射角(光疏介质中)和入射角(光密介质中)的关系满足正弦值之比等于常数(大于),而与两个重要的角度息息相关的便是三维波形切平面处的法线了。折射导致我们所观察到的点的位置并非其在水底的实际位置,而是从在一个符合某一规律的相对偏移量。我们的核心问题就是寻找计算相对偏移量的方法。在讨论三维波形之前先讨论相对简单的二维波形,下图是sin简谐波上的折射与相对偏移量的分析图:

显明的几何关系使得我们可以很容易地推导出Δx与x的关系:
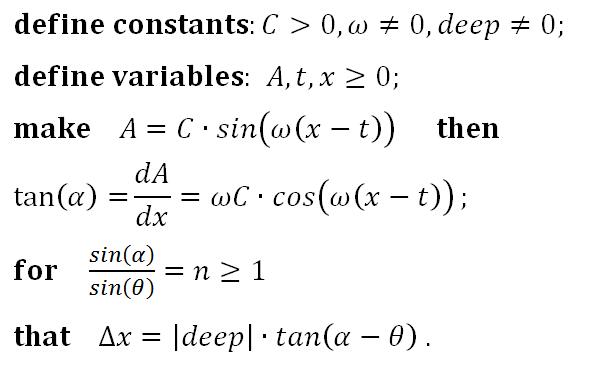
A代表x处的波的振幅,Omega参数用于调节波长,t决定某时刻的相位,deep实则表示水的深度,最终体现在折射的强度上。由几何关系易获得导数与折射偏移量之间的函数关系。值得注意的是,在计算Alpha角时需要用到反正切函数(开销较大),这里采用一种近似算法:
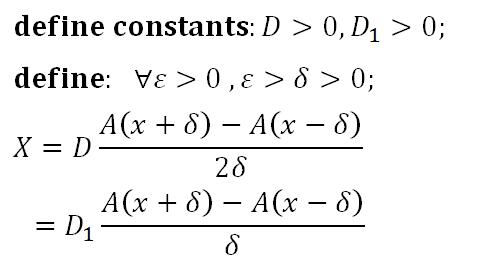
不难看出,当Epsilon很小时X与 具有一致的符号与单调性。若规定相邻两个像素点的距离为1,那么有:
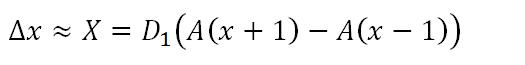
在这里,参数D1直接影响了折射的强度。
以上就是对二维波形上折射及相对偏移量的讨论了,我们已经得出的结论是x方向上的相对偏移量与在该方向上的导数存在函数关系。实际上,在三维波形上,相对偏移量无非就分为x方向和y方向的了,并且分量上的相对偏移量如二维波形上的关系一样,与波形函数的偏导数呈函数关系,这里不再证明。以下是推广过程:

同样地,采用近似计算法:
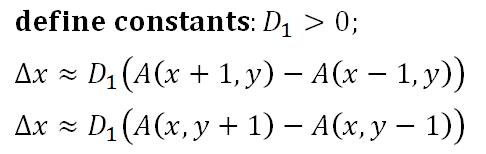
到这里,我们完全可以通过模拟三维波形并且计算相对偏移量了。本人并不了解windows编程,编程时为方便起见采用EasyX(也可采用OpenGL)绘图库注册窗口以及绘制图像,算法完全由C++编写。下图是模拟了单个波源产生的三维简谐波,用灰度值为255的蓝色和红色分别表示-1与+1:

在进行水纹渲染时,只需要将波形的数据存放在内存中供计算每个像素点的相对偏移即可。但实际的波形在传递过程中无疑会存在能量的衰减,否则即便无穷远处的波的振幅依然和波源一致,显然不合实际。接下来就讨论波的衰减吧。
所谓衰减,可以简单地认为是波源以外点的振幅(无衰减的)乘以一个该点随相对波源距离的增加而递减的因子。要建立严格符合物理定律的数学模型是一件麻烦的事,况且衰减本身也不是水纹渲染的核心问题,那么可以通过选取合适函数来近似模拟波形在传播中的衰减。对于衰减函数的选择,显然有以下重要约束条件:
1. 连续且单调递减
2. 定义域包含全体正实数
3. 函数值域为(0,1],且函数在无穷大处的极限为0
通过多次试验与对比,我最终选择的衰减模型为:
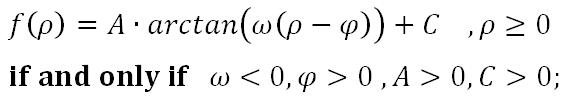
其中,常量A,C用于限定函数变换范围为[0,1];参数Omega小于零,使得函数变为 上的单调递减函数,其绝对值大小决定了衰减速率;参数Phi决定了函数在 上拐点的位置,其领域则是波形衰减最为明显的范围。由于该函数的性质使得生成波形衰减过程在期望区间内看上去相对自然,并不过于急剧或者缓慢。
到这里,或许你会觉得使用反正切函数无疑增加了运算开销,何不采用更为简单的函数呢?我的回答是:首先,为了渲染的美观。其次,衰减处理完全可以事先生成离散值的哈希表,调用时用参数Rho查询即可。

当然,也可以引入两个或以上的波源,与此同时也可以看出波形的干涉了:

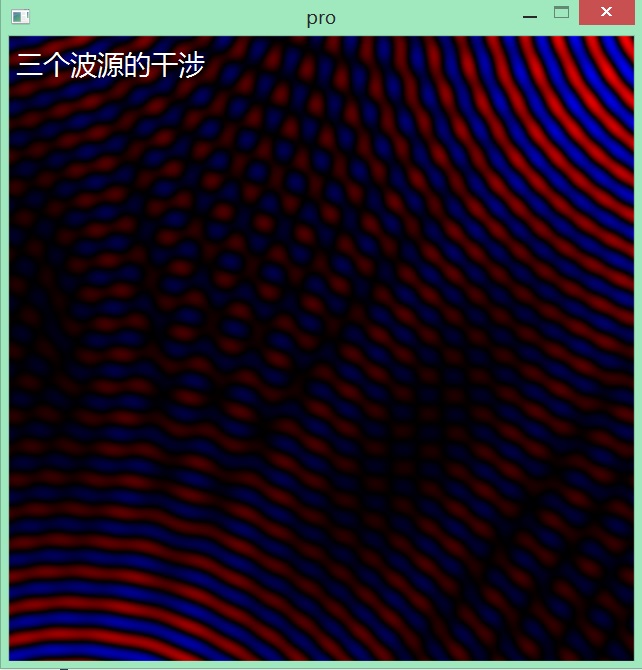
通过上述讨论,可以简单的建立一个渲染器模型:
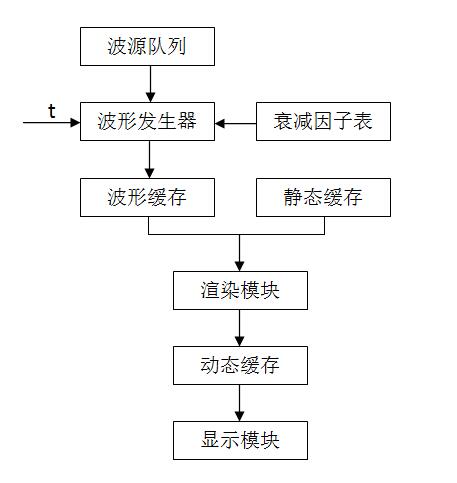
波源队列用于存放不同波源的参数,波形发生器通过获取波源参数与衰减因子来计算出显示区任意点处的波形并放入波形缓存,静态缓存中存放背景图像(水底的景物),每当处理好一帧的波形数据后交由渲染模块计算每个像素点的相对偏移量并生成图像存放到动态缓存中,最后由显示模块将生成的帧推送给显示设备。
以下就是最终实现的实际渲染效果与原图的对比:

居于正中的单的波源


波源在显示区外,可观察到明显的衰减


多个波源的综合测试
回顾水纹渲染的波形,每生成一帧的画面时需要更新显示区域的波形数据。每个像素点上的波的振幅是由它和波源的距离的函数所决定。假定只有一个波源的情况下,对于以同一波源为圆心,同一圆弧上的所有像素点的振幅是相同的。

Rho作为波形函数的自变量以及R所代表的几何意义让我们很容易理解点波源所产生的震荡在均匀二维介质中是以一系列间距相等的同心圆所构成。在圆的方程中,不同的R决定了满足方程的不同的点集。当R从0开始连续的增大至无穷时,那么圆弧的轨迹有且仅有一次覆盖了平面上所有的点。那么可以将不同的R和平面上互不相容的点集看做是一对一映射。这有什么用呢?之前说了,波形是以同心圆的方式传播的,如果我想要波形以同心的椭圆传播呢?首先来看椭圆方程:
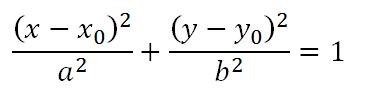
如果能像圆一样,找到一个可以当做Rho的参数R就好了。由于椭圆的形状和大小由参数a,b共同决定,不妨做如下改变:
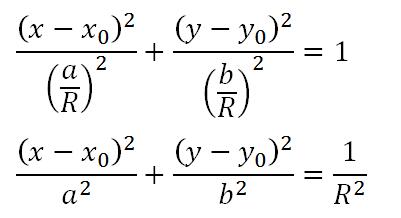
这样一来,椭圆的离心率并不会发生改变,从而形状不发生改变,但随着R取值不同,会得到不同大小的唯一的椭圆(相似的)。当参数R取值为全体正实数时,方程的解便可有且仅有一次覆盖整个平面。
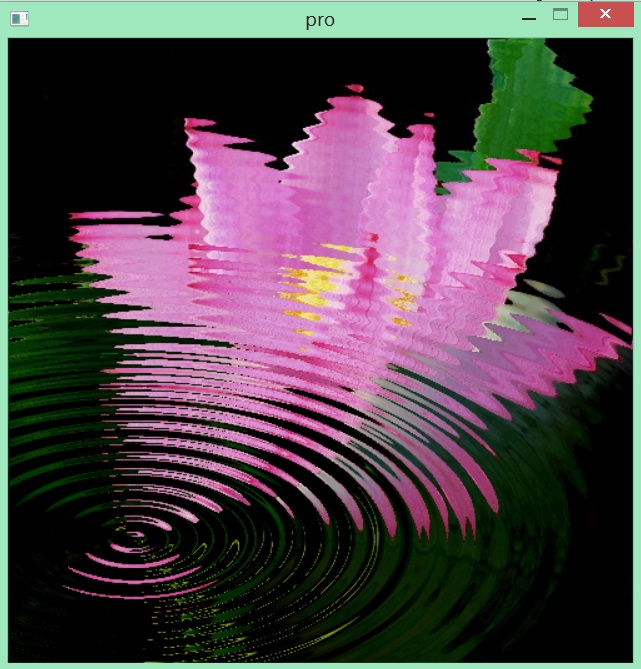
同样地,对双曲线也可采取相同的办法引入参数R,当然也可以做适当的处理使得离心率随R的变化而变化,但需要注意的是双曲线并不能覆盖全平面,即存在复数解,开方时需注意判定。
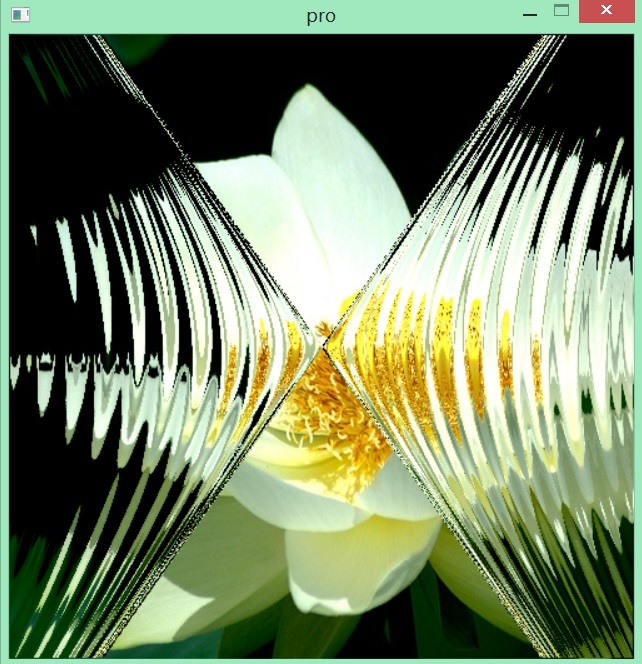
但是如果仅仅满足于将波形变换为椭圆或者双曲线那就太逊啦!试想一下照片上的水珠所产生的透镜效果,能实现吗?答案当然是肯定的!不过我们这次需要改变的是波函数。
照片上的水珠可以近似的看做是半个椭球体吧,那么将这半个椭球体的方程中解出z变量来不就可以看做波函数了吗?
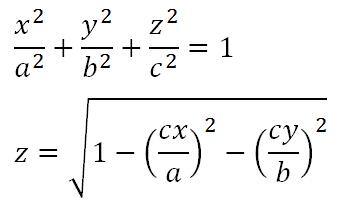
注意根号下必须大于或等于0。如下是水珠透镜的实现:

小结:一个看似复杂的问题,只要合理的去界定分析总会有所收获的。