机器学习--决策树

Decision Tree

目录

• Decision Tree
  • Pre:
  • Tree construction
  • Information Gain 信息增益
    • 1. 信息增益的计算
      • 1.1 信息（Information）:
      • 1.2 熵(entropy):
      • 1.3 信息增益(Information Gain):
      • *1.4 基尼不纯度（Gini impurity）：
  • Measuring consistency in a dataset
  • Using resursion to construct a decision tree
  • Plotting tress in Matplotlib

Pre:

如下图所示，决策树包含判断模块、终止模块。其中终止模块表示已得出结论。

相较于KNN，决策树的优势在于数据的形式很容易理解。

相关介绍

1. 奥卡姆剃刀原则: 切勿浪费较多的东西，去做‘用较少的的东西，同样可以做好的事情’。
2. 启发法:(heuristics,策略法)是指依据有限的知识（不完整的信心）在短时间内找到解决方案的一种技术。
3. ID3算法:(Iterative Dichotomiser3 迭代二叉树3代) 这个算法是建立在奥卡姆剃刀原则的基础上：越是小型的决策树越优于大的决策树（简单理论）。

Tree construction

General approach to decison trees

1. Collect : Any

2. Prepare : This tree-building algorithm works only on nominal values(标称型数据), so any continuous values will need to quantized（离散化）.

3. Analyze ：Any methods, need to visually inspect the tree after it is built.

4. Train : Construct a tree data structure.

5. Test : Calcuate the error rate with the learned tree

6. use : This can be used in any supervised learning task, often, trees used to better understand the data

   ——《Machine Learning in Action》

Information Gain 信息增益

信息增益：在划分数据之前之后信息发生的变化.
划分数据集的大原则是：(We chose to split our dataset in a way that make our unorganized data more organized)将无序的数据变得更加有序。

1. 信息增益的计算

Claude Shannon(克劳德.香农)
Claude Shannon is considered one of the smartest people of the twentieth century. In William Poundstone’s 2005 book Fortune’s Formula, he wrote this of Claude Shannon: “There were many at Bell Labs and MIT who compared Shannon’s insight to Ein-stein’s. Others found that comparison unfair—unfair to Shannon.”

1.1 信息（Information）:

• 信息多少的量度

[l(x_i)=log_2P(x_i)]

1.2 熵(entropy):

• 在吴军的《数学之美》中，认为信息熵的大小指的是，了解一件事情所需要付出的信息量是多少，这件事情的不确定性越大，要搞清楚它所需要的信息量就越大，信息熵也就越大。

加入一枚骰子的六个面只有1，那么投掷不会带来任何信息，其信息熵就是 0

• 在我看来，熵就是描述系统的有序化程度。有序化越低，可选择的就越少，在决策树中就越容易分类。反正。。。。

• 公式：

[{H}(x)=sum_{i=1}^{n}{P}(i){I}(x_i)= -sum_{i=1}^{n}{P}(x_i)log_b{P}(x_i)]

代码：

#-*- encoding:utf-8-*-
# Function to calcuate the Shannon Entropy of a dataset
# 
from math import log 
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    # create a dictionary of all posssible classes
    for  featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0  #??
           #labelCounts[currentLabel] = 1 
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for  key in labelCounts:
        prob = float(labelCounts[key]/numEntries)
        shannonEnt -= prob * log (prob,2)
    return shannonEnt 

实例计算：

首先根据上图创建一个数据集

#-*-encoding=utf-8-*-
# filename : createDataSet.py
# utilizing the createDataSet()function
# The simple data about fish identification from marine animal data 
def createDataSet():
    dataSet = [[1,1,'yes'],
    [1,1,'yes'],
    [1,0,'no'],
    [0,1,'no'],
    [0,1,'no']]

    labels = ['no surfacing','flippers']
    return dataSet, label

使用计算熵方法计算该数据集的熵：

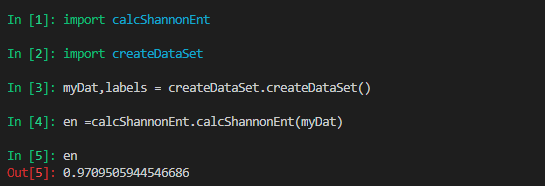
如若修改上述数据集,得到的结果为：

一个系统越是有序，信息熵就越低；反正，一个系统越混乱，信息熵就越高。

1.3 信息增益(Information Gain):

在决策树中，关键的是如何选择最有划分属性，一般来说，我们希望划分后分支节点所含的样本尽量属于同一类节点，即节点的的纯度越高越好。

• 数据集划分

根据不同属性将数据集划分子集
代码：

 #-*- encoding=utf-8 -*-
# split the dataSet
'''
this function split very feature from the dataset then to calculate the Information Gain sperately
dataSet: the dateset will be splited
axis :
value: the value of the feature to return 
the difference between extend() and append()
a= [1,2,3]
b= [4,5,6]
a.append(b)
a = [1,2,3,[4,5,6]]
a.extend(b)
a = [1,2,3,4,5,6]
'''
def splitDataSet(dataSet,axis,value):
    # create a new list
    retDataSet = []
    for featVec in dataSet:
        # cut out the feature split on 
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

不同划分的结果:

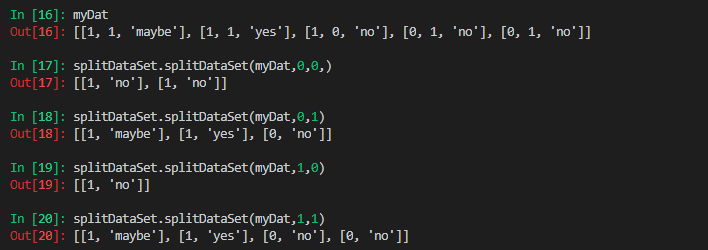
从上图可以看出当使用属性0划分时结果更合理；

• 计算最佳划分的特性：

#-*-encoding=utf-8-*-
'''
set()
'''
import calcShannonEnt
import splitDataSet 
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) -1
    baseEntroy = calcShannonEnt.calcShannonEnt(dataSet)
    baseInfoGain = 0.0
    bestFeature = -1
    bestInfoGain = 0.0  
    for i in range (numFeatures):
        featureList = [example[i] for example in dataSet]
        #create a unique list of class labels
        uniqueVals = set(featureList)
        newEntropy = 0.0
        for value in uniqueVals :
            subDataSet =splitDataSet.splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt.calcShannonEnt(subDataSet) #划分后的信息熵 不同子集的信息熵和该子集的概率的之和。
        infoGain = baseEntroy - newEntropy #信息增益
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature
mydat, label = createDataSet.createDataSet()
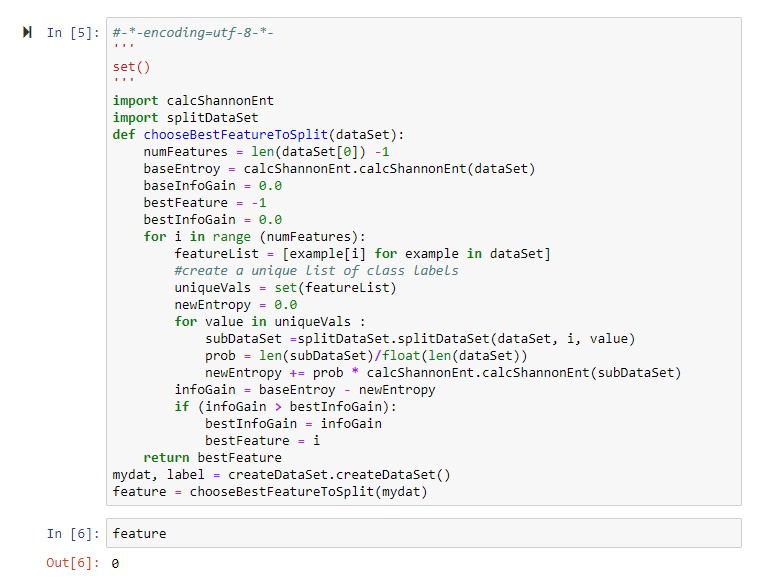
feature = chooseBestFeatureToSplit(mydat)

其结果显示第一个划分节点为特性0时所计算的信息增益更大

参考文章：https://www.cnblogs.com/qcloud1001/p/6735352.html

*1.4 基尼不纯度（Gini impurity）：

Measuring consistency in a dataset

Using resursion to construct a decision tree

Plotting tress in Matplotlib