线性规划中的单纯形法与内点法（原理、步骤以及matlab实现）（一）

线性规划(Linear Programming Problem:LPP)是凸优化以及现实生活中经常遇到的问题，解决线性规划问题常用的方法有单纯形法(Simlex Method)（普通单纯形法，大M法，两阶段法，对偶单纯形法）以及内点法(karmarkar method)

matlab中求解线性规划使用 linprog(f, A, b, Aeq, beq, lb, ub)以及revised(c, b, a, inq, 1)

注：f为目标函数（min形式）系数矩阵，A为限制条件系数矩阵，b为右端值矩阵（元素可以小于零），Aeq为等式约束的系数矩阵，beq为等式约束的右端值矩阵，lb和ub为未知数的下限和上限

1.LPP 

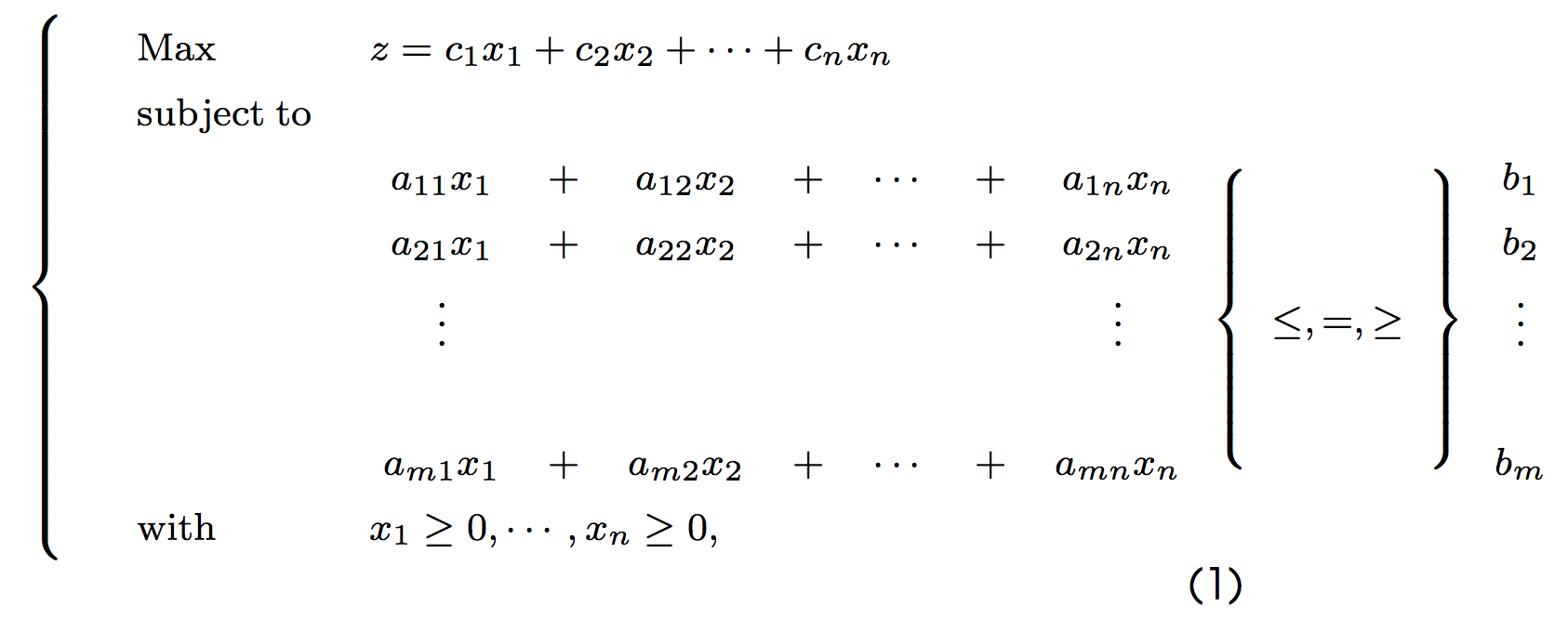
2.Simplex Method

每一次迭代的tableau 格式如下：

=====================================================================

=====================================================================

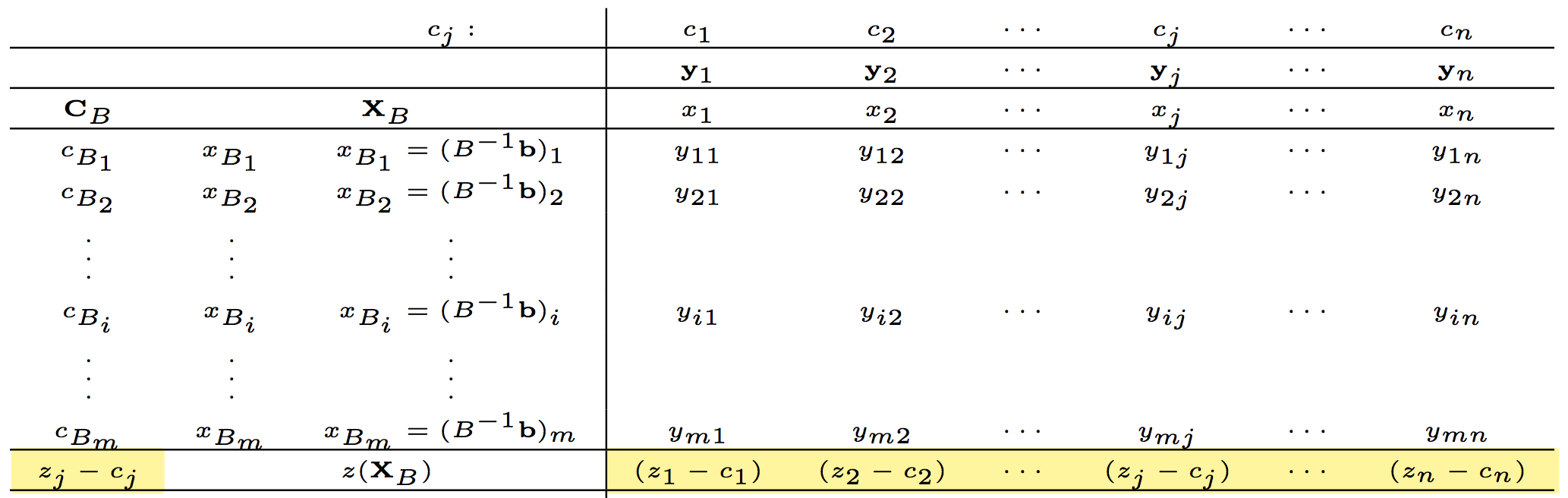
换入基、换出基的选择：

原理：

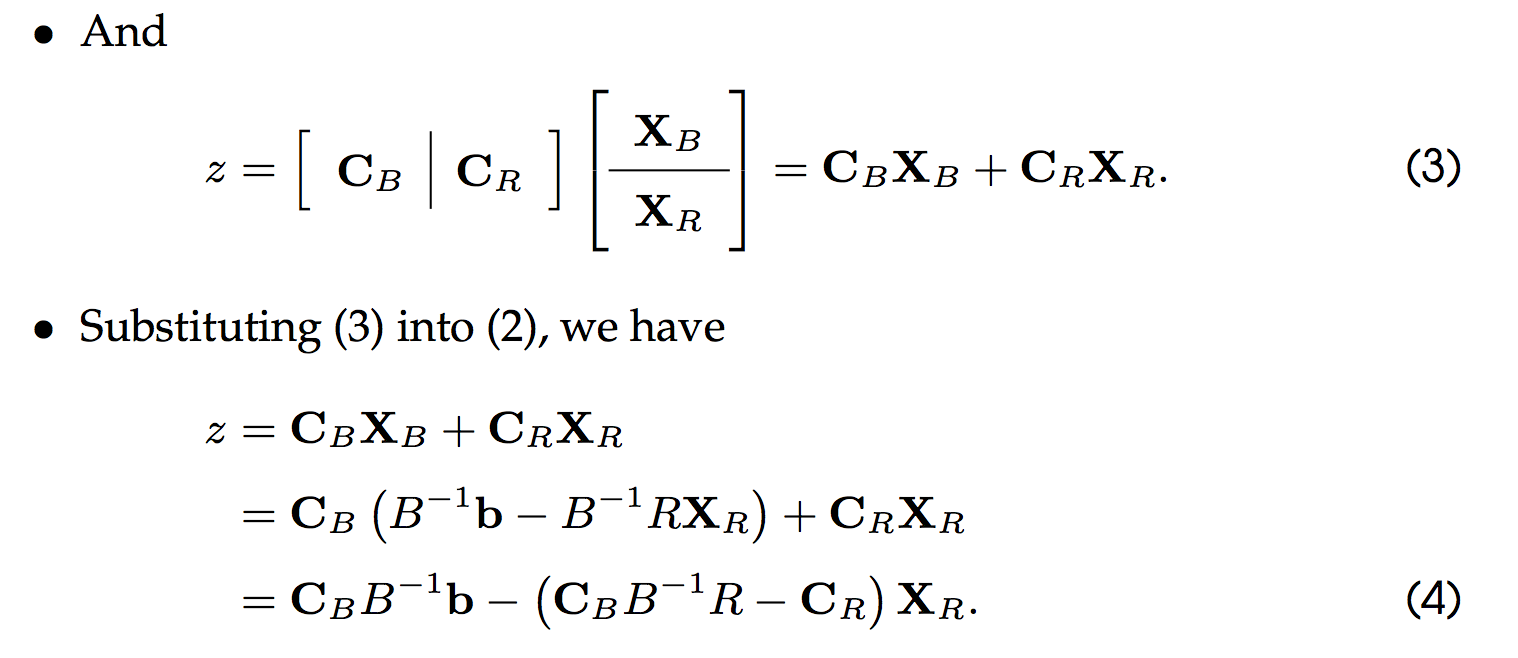
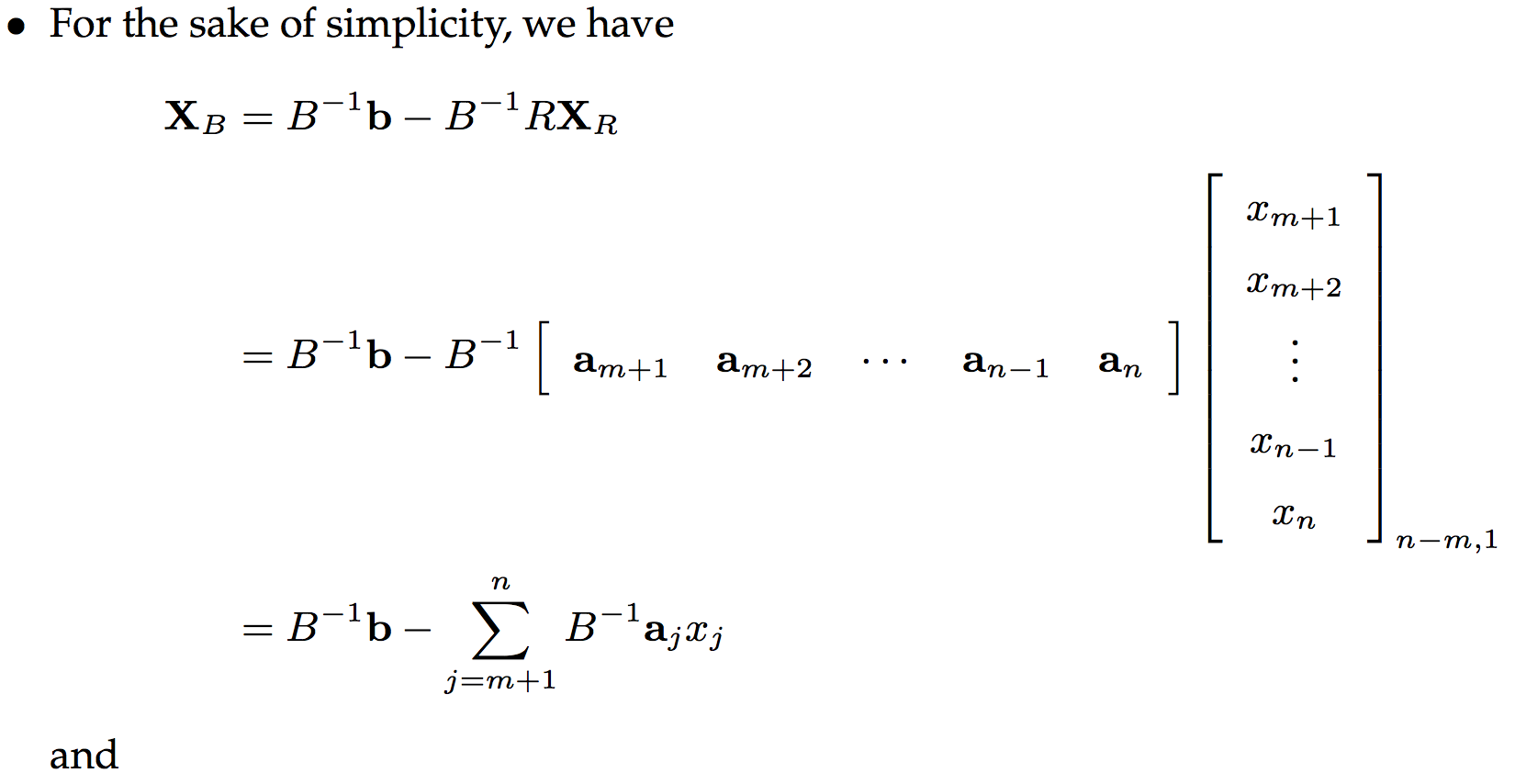
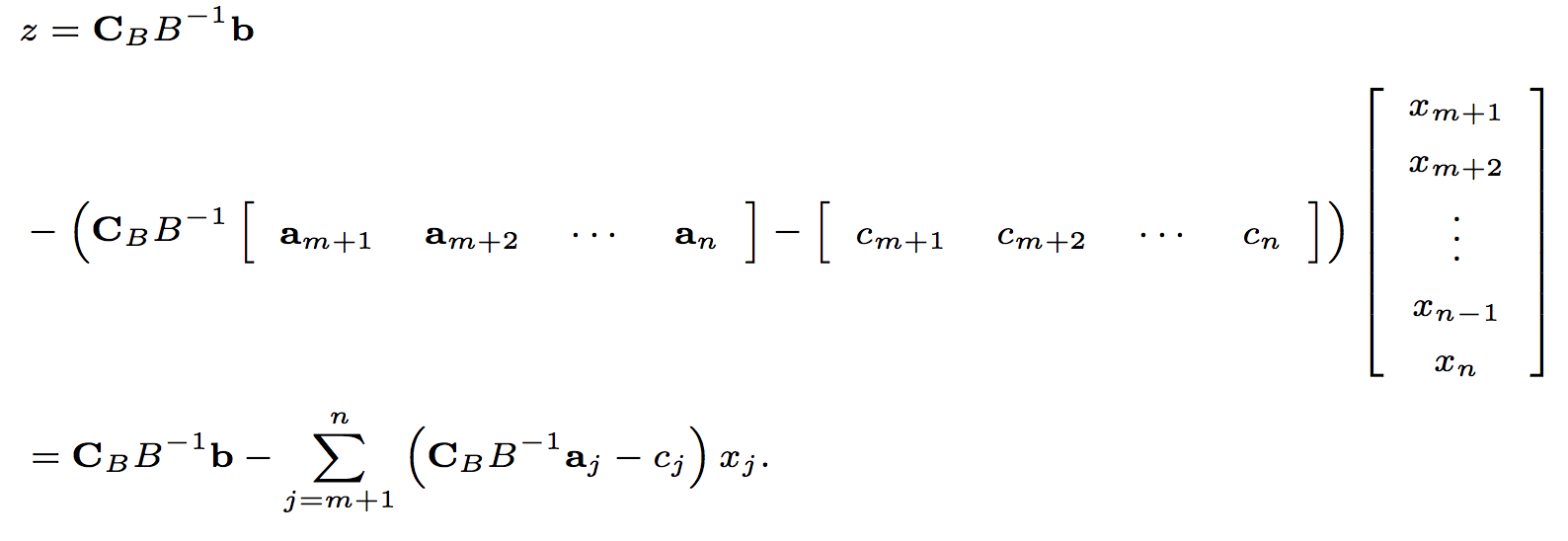
所以标准型可以换成以下的形式：

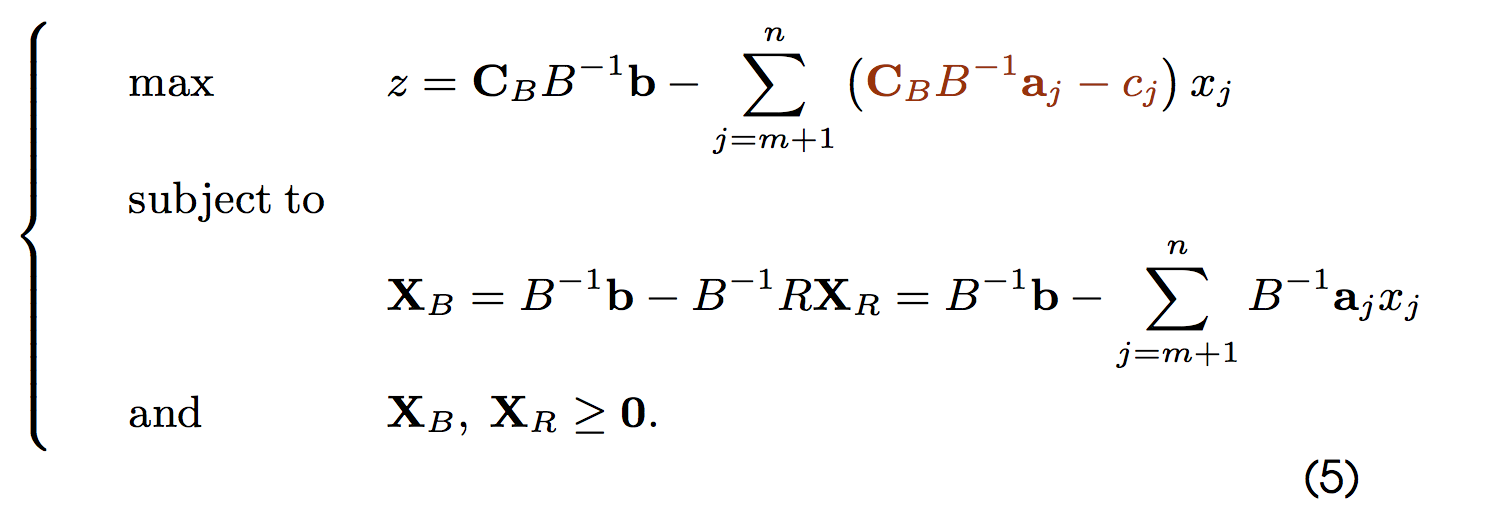
迭代的思想：

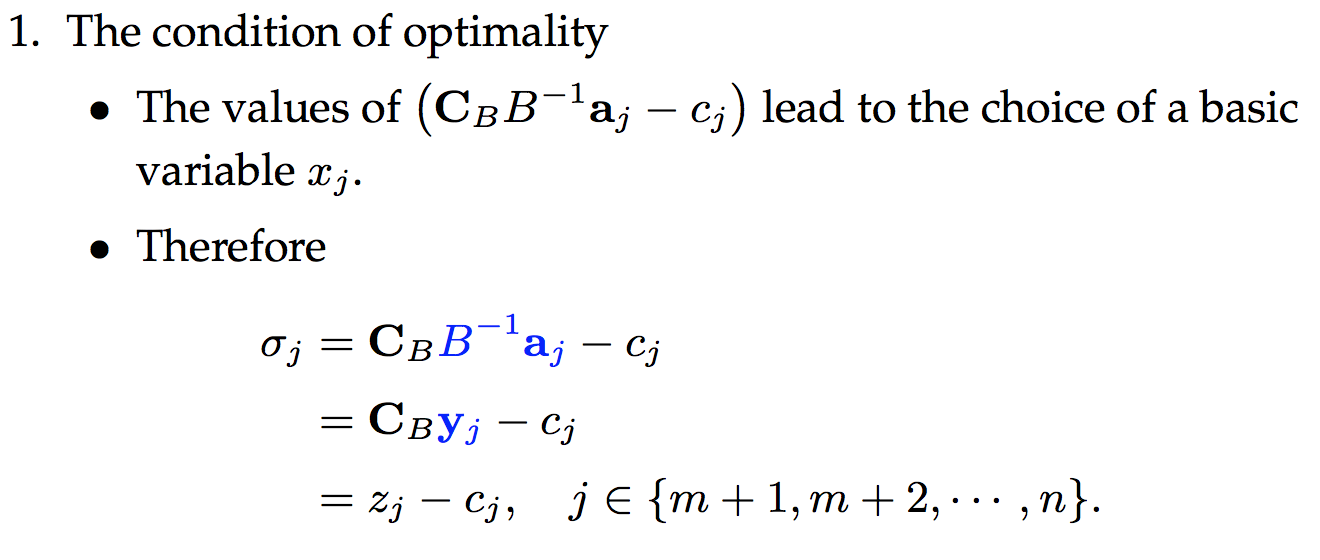
解的情况讨论：

 

========================================================================

========================================================================

2.1 Simplified Simplex Method (普通单纯形)

LPP中的约束条件全是等式约束

standard form

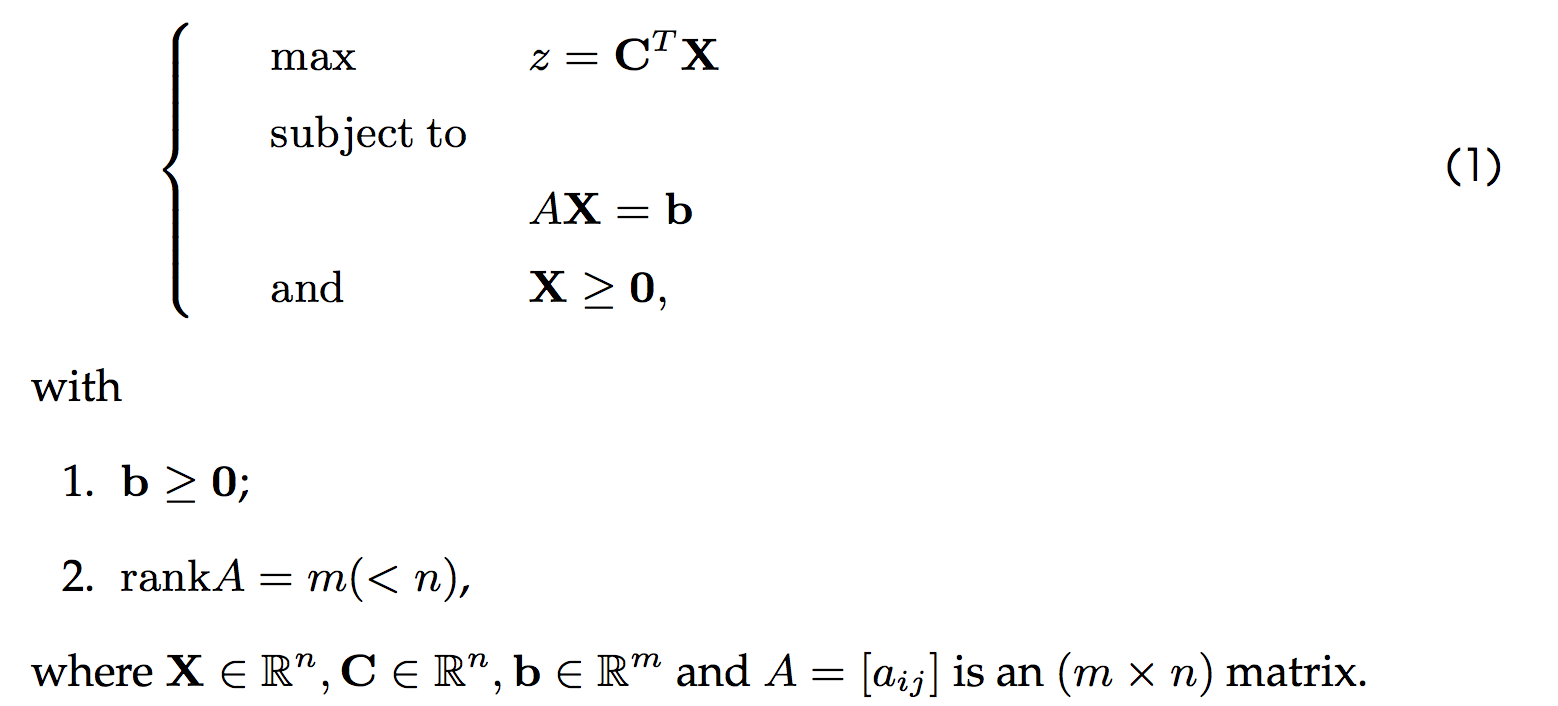
 注：这里的右端值b必须全部非负

 下面举例说明该种方法的应用以及matlab的两种实现

Solution 

首先引入变量(slack or surplus)将原问题转为标准格式：

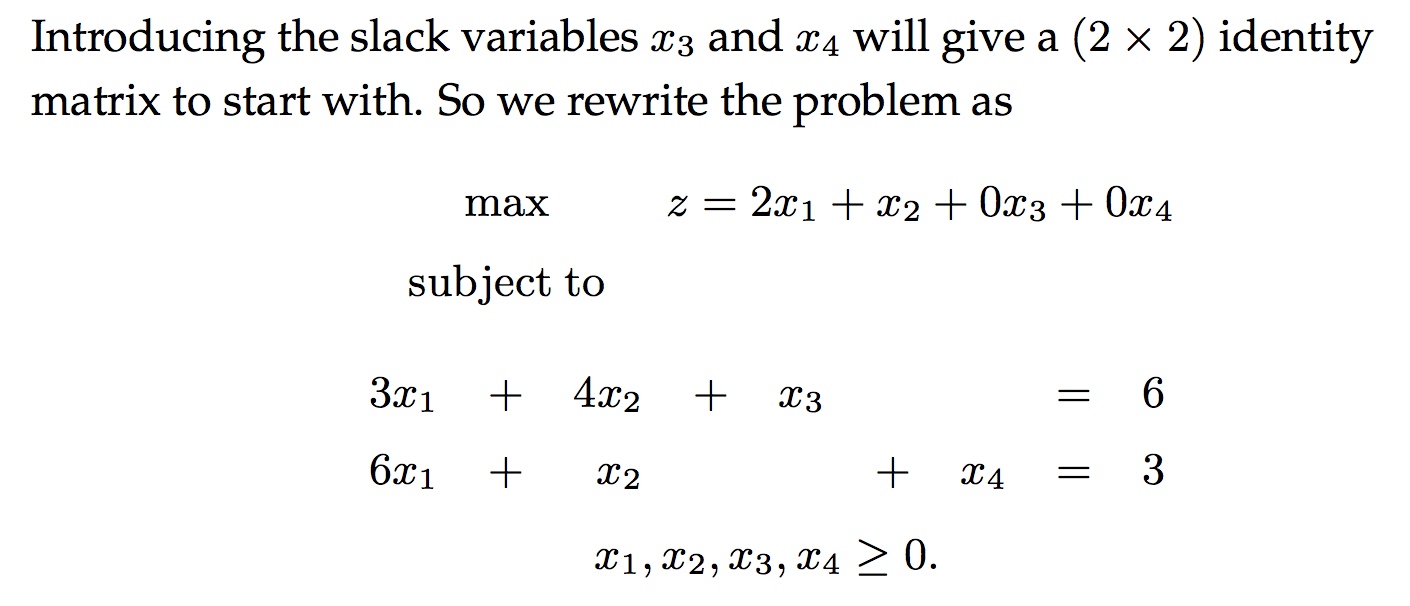
下面开始迭代：

first tableau

 

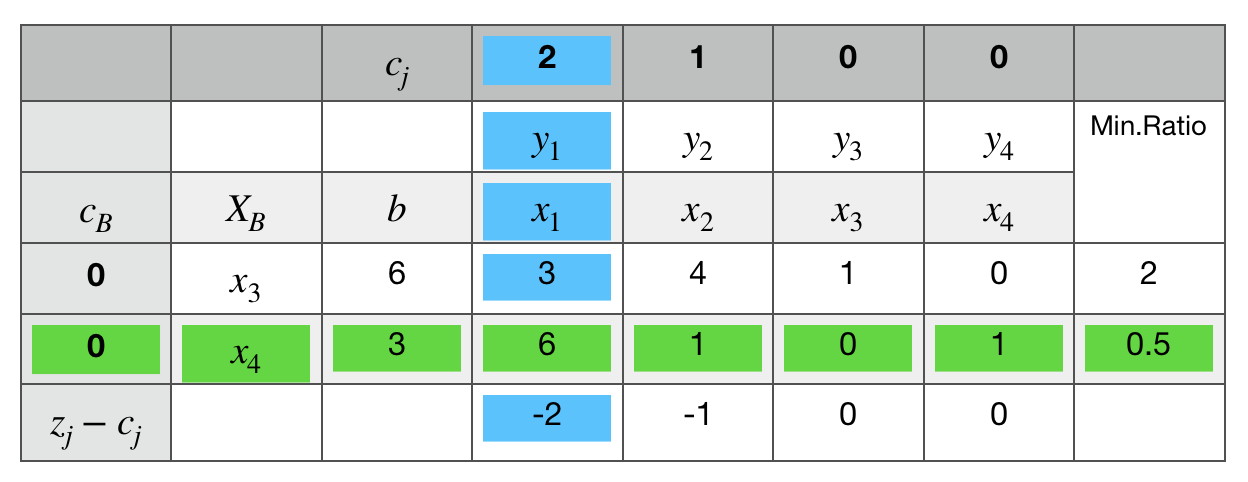
将x1作为基变量换出x4

second tableau

将x2作为基变量换出x3

third tableau

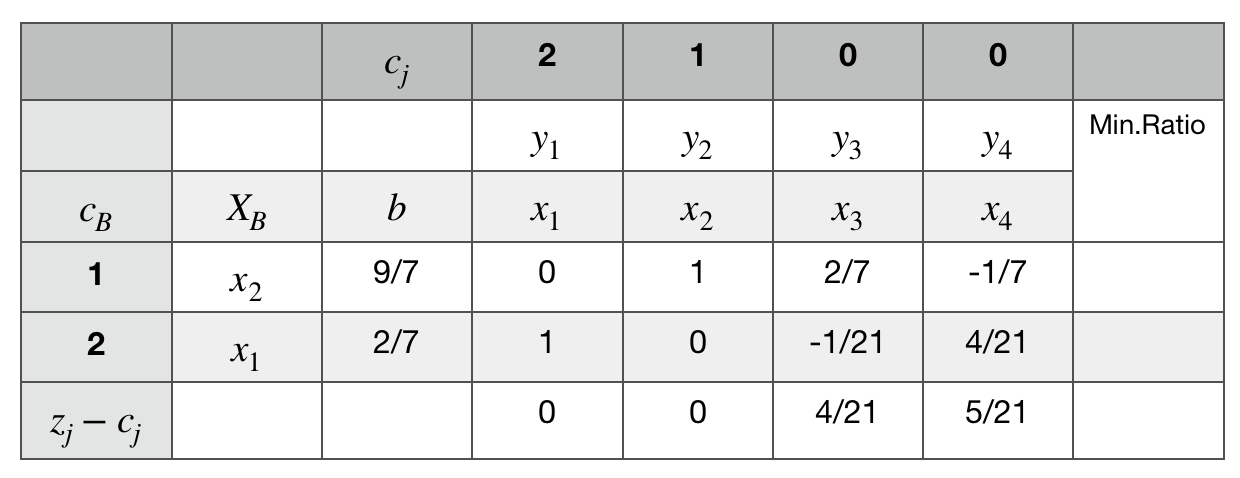
可以看到

所有的z_j-c_j都是非负的，所以此时的x值是最优值，答案为：

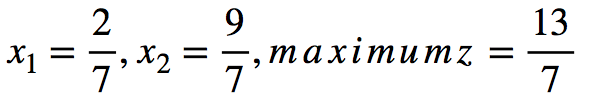
matlab实现

linprog() : 

注意：linprog()解决问题的标准格式如下：

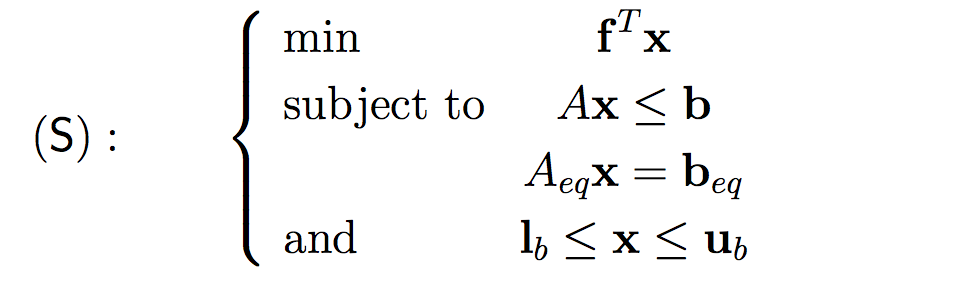
所以需要转换原问题为最小化问题！！！

f = [-2, -1];
A = [3 4; 6 1];
b = [6 3];
[x, fval] = linprog(f, A, b)

 下面贴出运行结果

revised():

注意：该函数不是内置函数，需要自行下载函数，附上网址：http://cn.mathworks.com/matlabcentral/fileexchange/26554-revised-simplex-method?focused=5147615&tab=function

c = [2 1];
A = [3 4; 6 1];
b = [6 3];
inq = [-1 -1];
revised(c, b, A, inq, 0)