=================2017-11-08==============
MATLAB版本低,没有求hessian矩阵的函数,写了一个,需要的拿走
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% --------------------------
%INPUT
%f: funtion;
%X: variables vactor;
%--------------------------
%OUTPUT
%H: Hessian matrix
%--------------------------
%Example
%syms x y z
%f = x^2 + y^2 + z^2;
%X = [x, y, z];
%H = hessian(f, X)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
funtion H = hessian(f, X)
H = zeros(length(X));
for i = 1: length(X)
df1 = diff(f, X(i));
for j = 1: length(X)
df2 = diff(df1, X(j));
H(i, j) = df2;
end
end
======================给一个求偏导,也就是第一步解偏导方程等于0的函数===================
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% --------------------------
%INPUT
%f: funtion;
%X: variables vactor;
%--------------------------
%OUTPUT
%op: optimal point
%--------------------------
%Example
%f = 2*x1^2 - 24 * x1 + 2 * x2^2 - 8*x2 + 2 * x3^2- 12*x3 + 200;
%X = [x1, x2, x3];
%op = first_condition(f, X)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function op = first_condition(f, X)
constraint = [];
for i = 1: length(X)
df = diff(f, X(i));
constraint = [constraint, df];
end
op1 = solve(constraint);
op = [];
for i = 1: length(X)
s = ['op1.' char(X(i))];
a = eval(s);
op = [op, a];
end
disp(constraint.')
===========================下面给出用法和输出================
比如说求![]() 极值,第一步是偏导等于零的点
极值,第一步是偏导等于零的点
给出代码如下:
syms x1 x2 x3 f = 2*x1^2 - 24 * x1 + 2 * x2^2 - 8*x2 + 2 * x3^2- 12*x3 + 200; X = [x1, x2, x3]; op = first_condition(f, X)
输出结果:
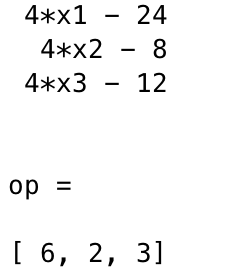
就是说在点(6, 2, 3)处取极值
============================更==========================
我们这一次对二次型进行更深的讨论
讨论多变量的正定型、负定型和半正定、半负定
先给出结论:
判断有两种方法:
1.强推特征值法:如果所有的特征值是正,则是正定型;全是负的就是负定型;全是非负,就是半正定型;全是非正,就是半负定型;
2.子式判断法:分两步:
第一步:所有阶的主子式大于0,就是正定型;奇数阶的主子式小于0并且偶数阶的主子式大于0,就是负定型;所有阶的主子式大于等于0或者奇数阶的主子式小于等于0并且偶数阶的主子式大于等于0,转入第二步;除此之外的都是不定型;
第二步:所有阶的子式大于等于0,就是半正定型;奇数阶的子式小于等于0并且偶数阶的子式大于等于0,就是半负定型


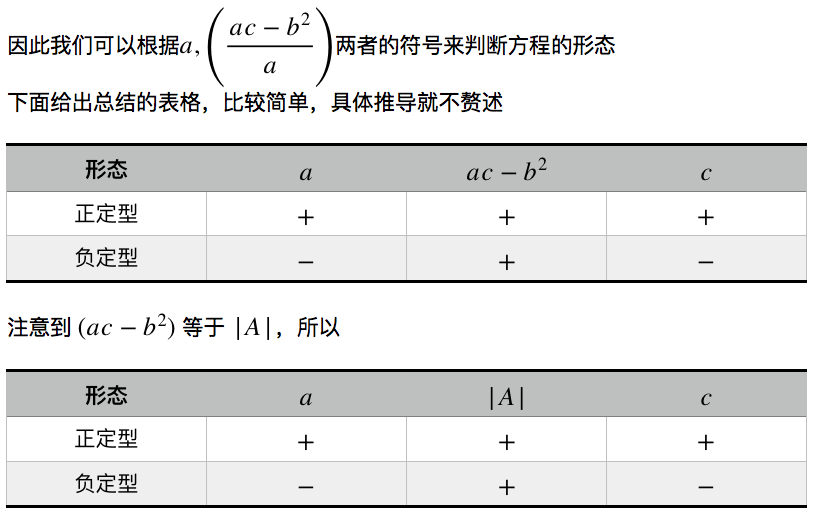
在继续下面的讨论时,我想先插入一小段关于相关矩阵的一些说明



