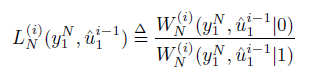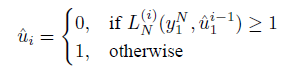一个好码必须具备两个要素:可靠、高效。
高效的码要求码的编译方案都具有较低的复杂度。极化码出现后,Arikan本人提出使用SC译码方案来进行译码操作。SC全称successive cancellation decoder,即连续消除译码。SC译码采用蝶形算法,通过递归的方式进行串行解码,其优点在于算法复杂度较低,缺点是无法进行并行解码(并行解码可以提高解码速度)。对于polar code的解码,还有几种常用方案:BP解码、SCL解码、SCAN解码等,本系列我们重点来介绍SC译码。
SC译码算法中有这样两个比较重要的名词。
- 似然值
似然值(“Likelihood Ratio”缩写LR),其定义在Arikan论文中为:
公式乍一看很复杂,其实很好解释,LR的值就是在接收端得到(
)时,发送端原本发送“0”的概率与发送“1”的概率之比。显然,如果LR>1,意味着原本发送“0”的概率要大一点,于是我们判决这个接收端应该收到的信号为“0”,反之为“1”。
不过别忘了,在我们发送的信息之中,有一部分位是没有信息量的即冻结位,这一部分我们假如默认全为“0”的话,那么即使似然判决结果为LR≤1,我们也强制要求它为“0”。这个判决步骤被形象的称为“硬判决”,自然,上面的判决就称作“软判决”。
- 误码率
经过判决之后,我们在接收端得到了一组完整的二进制数,再将这组数与原本发送的数逐个对比,如果有不一样的位,说明我们的解码出现了误码,此时我们统计出错位数,计算BER(bit error ratio,比特误码率)、FER(frame error ratio,误帧率),BLER(block error ratio,误块率),PER(package error ratio,包错误率或丢包率),这些参数是衡量一种解码方案乃至仿真系统性能的重要指标。通过以SNR(dB)为横坐标,上述参数为纵坐标绘制折线图,我们可以很直观的对比不同解码方案的性能。
由于解码方案的matlab实现相对来说较为复杂,因此为了方便梳理思路以及帮助大家理解,仿真过程全部以码长为N=8为例进行解释,不过程序的编写过程中充分考虑了所有码长下的情况,只需更改程序开头预定义的N值,即可实现任意码长的编解码仿真。本节我们只探讨第一和第二个解码器的解码过程,剩下的我们放到以后的各章节中解释。
SC解码方案中两个核心的要素,一是递推公式,二是蝶形算法。先奉上看起来高深莫测的递推公式和蝶形图。
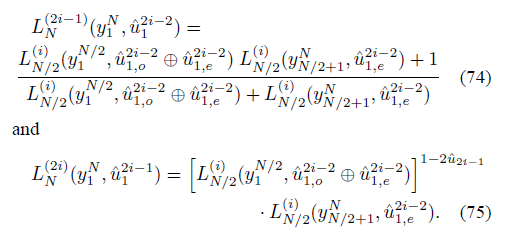
其实这个递推公式也很好理解,比较烦的就是里面各种下标的引用。大家可以看到,公式中有一些看起来比较奇怪的参数,这里做一下说明。
比如
,代表一个向量
。
比如
,同样表示一个向量,只不过下标(1,o)表示这个向量只包含 1~2i-1 中的奇数项(奇数,odd),同理如果是(1,e)的话,表示包含偶数项(偶数,even)。
分析这个递推公式,它包含两个公式。仔细观察 L的上下标,发现第一个递推公式用来计算 L 的奇数项,第二个公式用来计算 L 的偶数项。其实这种分类更深层次的意义在于区分蝶形算法的上下节点。为了方便表示,我们将递推公式和蝶形图简化表示:
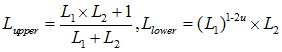
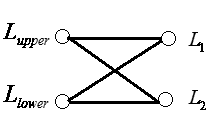
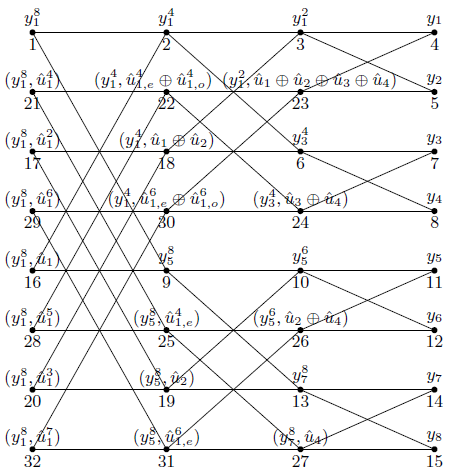
如上蝶形图,我们在解码的时候,是从右向左进行解码的,在得到右边两个节点之后,我们才能利用Arikan递推公式求解左边两个节点。其中上节点用第一个公式求解,下节点用第二个公式求解。观察第二个公式,L1有一个指数项(1-2u),每一次计算下节点的时候都需要额外计算指数项。另外,蝶形算法有一个规律,即每一次求解蝶形上的节点时,上下两个节点总是同时被解出。举个栗子,以上图为例,如果我们在求解过程中,发现 L1的似然值已经被求出来了,那么不用看我们就能肯定的说,L2一定也被解出来了。
我们来看第一第二个节点的代码实现。首先是预定义数组。
mem_lr = zeros(N, n+1); % 定义似然值矩阵用于储存所有节点的似然值,其中N=2^n;

如上图,节点1为判决器1,节点16为判决器2。(为什么?还记得我们上一节提到的反序重排矩阵BN吗?没错,最初的时候判决器的行序是u1~u8,反序重排以后,u2就放在了u5的位置上,u1则保持不变)红线凸出的部分所经过的节点就是我们为求得u1、u2所必须求出似然值的节点。解码从最右端开始,这个时候我们必须知道y1~y8的似然值,才能计算左边节点的值。Arikan给出的计算公式为:

W(y|x) 为信道转移概率,由于我们是在高斯信道下进行仿真,所以 W(y|x)服从高斯分布,其计算公式为:
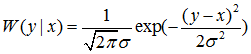
上式中的均值 x 取值 1 、-1(为什么? 这个地方需要再一次温习编码中的一个步骤:在编码的最后,我们对编码矩阵对2取模,然后符号化,才与噪声进行叠加。因此,这里其实相当于将 0 替换为 -1)。将 x=-1、x=1,带入上式,将得到的 W 带入似然值公式做分式运算,得到:
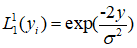
其中,y即为叠加噪声后的接收端信息。由于snr=m2/σ2(信噪比定义)且 m2=1。将上式中的σ换算成SNR带入,可以得到:
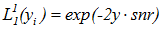
接下来的工作,先是循环求出最后一列所有节点的似然值,然后从最后一列开始倒推计算似然值,发现一个现象:计算u1用到的所有节点都位于上节点,因此只需迭代调用第一个公式就能计算出u1:
for ii=0:1:n
if ii==0
for j=1:2^n
mem_lr(j,n+1)=exp(-2*encode((r_idx-1)*N+j)*snr(i)) % r_idx取值为(1:block),i用来遍历信噪比矩阵,这两个变量在这段程序中相当于外部变量
end %计算最后一列似然值
else
for j=1:2^(n-ii)
mem_lr(2^ii*(j-1)+1,n+1-ii) = (mem_lr(2^ii*(j-1)+1,n-ii+2) * mem_lr(2^ii*(j-1)+1+2^(ii-1),n-ii+2) + 1) /...
(mem_lr(2^ii*(j-1)+1,n-ii+2) + mem_lr(2^ii*(j-1)+2^(ii-1)+1,n-ii+2));
end % 从最后一列循环迭代使用第一个公式倒推计算节点似然值
end
end
通过上面的程序可以得到u1对应节点的似然值,可以对其进行判决:
k = find(frozen_index == 1) % 查看u1是否为冻结位 if isempty(k) % 如果k为空矩阵,即u1不是冻结位 if mem_lr(1,1) < 1 decode((r_idx-1)*N+1) = 1; % r_idx表示此时程序锁操作的信息块,r_idx取值:1~block,下面不再强调 end % 软判决 else % 否则,u1是信息位 decode((r_idx-1)*N+1) = frozen((r_idx-1)*F+k); % 硬判决 end
u1计算完毕。
u2位于似然值矩阵第5行,且位于蝶形下节点。求解u2时,使用第二个递推公式,需要考虑指数项。观察上面红线标注的蝶形图,可以发现,用于计算u2的两个节点在求解u1的过程中已经全部求出,因此只需调用一次递推公式即可求出u2。这也就是为什么上面说,位于蝶形左上、左下节点的两个节点总是同时被解出。
关于前后级节点的下标关系:设当前节点坐标为(i,j),若当前节点未左上蝶形,则这个节点开启的两个节点的坐标为(i,j+1)和(i+N/2j,j+1)。若为左下节点,则这两个节点开启的两个节点坐标为(i,j+1)和(i-N/2j,j+1)。由此可以知道计算u2需要哪两个节点。根据递推公式,计算u2的指数项为(1-2u1),代码如下:
mem_lr(5,1) = (mem_lr(5-2^(n-1),2))^(1-2*decode((r_idx-1)*N+1))*(mem_lr(reverse_idx,2)); % 递推公式二,计算u2的似然值
同理,对其进行似然判决:
k = find(frozen_index == 2) % 查看u2是否为冻结位 if isempty(k) % 如果k为空矩阵,即u2不是冻结位 if mem_lr(5,1) < 1 decode((r_idx-1)*N+2) = 1; end % 软判决 else % 否则,u2是信息位 decode((r_idx-1)*N+1) = frozen((r_idx-1)*F+k); % 硬判决 end
经过以上步骤,我们得到了u1、u2的解码结果,简单的了解了SC译码的过程,下面来总结一下:
1、SC的译码分为两部分,左上节点和左下节点,其中左下节点的求解需要预先求解指数项,这个步骤在这里不够明显,但是之后会占用很大的篇幅。
2、SC译码时左上节点和左下节点总是同时被解出。
3、SC译码总是先求解左上节点,再求解左下节点。左上节点的求解是一个递推和迭代的过程。
4、判决分为似然判决和硬判决。
经过这一节的介绍,大家对SC译码的过程有了简单的认识,下一节中,我们会尝试将u1、u2的求解模式抽象为一个固定的程式并推广到整个蝶形图中,使得SC译码算法更为符合for循环结构,以便编写形式简洁优美的代码。
敬请期待!