咱也不敢写总结只能说小结因为到现在会的还是太少
也不说自己弱了因为即使是真的说了又有什么用呢
还是老老实实自闭吧
一,最大流
《士兵占领》:最大流的板子,但是一开始想偏了。正解是用最大流求出并集,然后用全集减掉。
《紧急疏散》:需要考虑的问题是每个门在一秒只能出一个人,用到一个拆点的思想。
按照时间拆点,然后在各个空地建出下一个时间的自己和周围的点连边。
二,最小割
感觉最小割要比最大流多一些。。。
《狼抓兔子》:网络流是用来写暴力的但是可A。。
《最大获利》:算是一个常见模型,大概长这个样子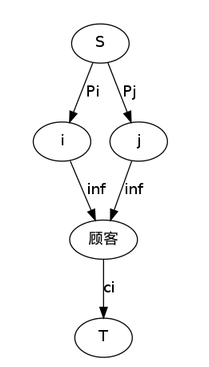
《happiness》:学到的一个技巧,因为题中是一个类似“联动权值”的东西,但还是有二分图的影子,于是大概这样。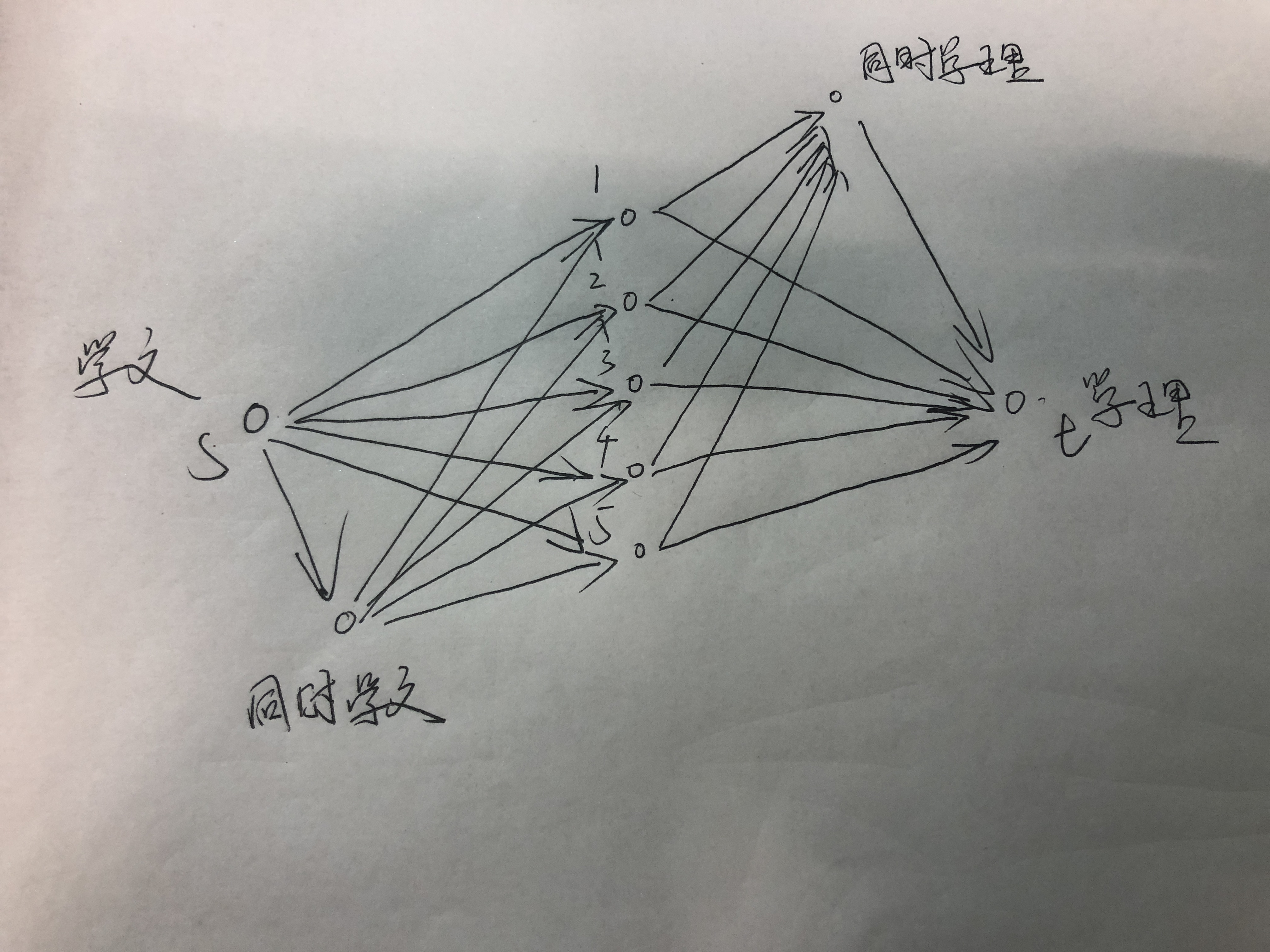
图是偷的所以看起来特别大23333
这样建图感性理解一下大概是可以解决问题的。
《人员雇佣》:大概题意是“两个都不割减2e,割一个减3e”。
乍一看感觉特别不可做,但是我们考虑在两点之间连边来表示两点之间关系,大概长这样。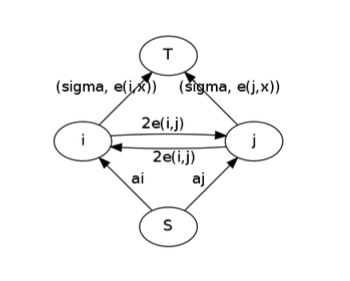
然后我们就解决了这类问题。
《切糕》:这道题是我在没读清题的时候就看到了类似的题解,虽然题解没看仔细,但是记住了图,然后在考场上推出来的。
既然有高度限制,我们就考虑通过建边来表示这个限制。
每个点只需要建一条边,因为会有一个类似“相互制约”的东西。
《线性代数》:化简一下柿子就能找到建图方法,还可以。
《千钧一发》:根据题目可以发现,奇和奇以及偶和偶之间不会连边,于是二分图。
《寿司餐厅》:肛道理这个应该开个新的叫最大权闭合子图,但是我太懒了。
按照限制要求(x-1,y),(y-1,x)向(x,y)连边,然后对于新的mx2的贡献新建点即可。
三,费用流
《晨跑》:费用流的板子。
《修车》:每个人做出的贡献是 自己前面修车总时间+自己修车所用时间
转换一下问题,变成了 当自己为倒数第i个修车时,作出的贡献为i*自己修车所用时间
然后按照时间拆点,边权直接为时间*边权即可
《美食节》:因为点数过多而导致时间复杂度会伪。
每次只会增广一个厨师的一道菜,于是每用完一个厨师加一个点。
写的时候不小心出了负环,原因是新加入的边的边权比之前流过的边权小。
但是上文所说的做法可以完美避开这一问题。
《数字配对》:题目中给出的限制条件有时更是建图的特殊性质。
考虑分层,因为每一个数字只能参与一次配对,所以要将配对和被配对和起来考虑,不然很难做。
根据题目发现可以按照质因子个数的奇偶分层,这样就可以把配对和被配对合起来。
四,上下界
《80人环游世界》&《星际竞速》:本来是最小费用最大流的题目,但是用上下界可水
《支线剧情》:大概上下界可行流裸题?
《清理雪道》&《旅行时的困惑》:上下界最小流。统计答案是用建出的S-->T的流量减去T-->S的最大流。还需要再理解一下。
《志愿者招募》:建图大概是这样。此时S=1,T=4。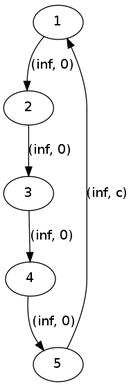
我听说了一个叫作“一面对多面”,大概就是类似一个区间加,然后见图用到了循环流的思想。
解释一下,按照时间将每一天连起来,边权为正常上下界。
为了保证正常流量,于是可以从T+1连一条到S的边,让这1流量流完区间。
《矩阵》:二分答案验证上下界可行流。
五,对偶图
《海拔》:观察题目可以得到性质是高度只有0和1,根据原图搞最小割是90分。
发现可以转换成对偶图的形式,运用对偶图性质求解,即最小割==最短路。
对偶图大概是将各个边将平面分成的区域作为点,然后按照图连边跑最短路。
说实在的到现在对偶图几个比较好的性质也没能搞清楚。
做了这个专题,觉得差距好像稍微有点大,于是就开始自闭了。