Day4 图论

并查集

并查集保持一组不相交的动态集合S={S1,S2,…,Sk}。
每个集合通过一个代表来识别。
代表就是集合中的某个成员。
哪一个成员被选做代表是无所谓的。
我们关心的是如果寻找某一动态集合的代表两次，并且在两次寻找之间不修改集合，两次得到的答案应该是相同的。

并查集的操作

• 初始化 Make-Set(x)

​ 建立一个新的集合，其唯一成员，就是x自己。

​ 因为各集合是不相交的，故要求x没有在其他集合中出现过。

• 合并 Union(x,y)

  将包含x和y的动态集合合为一个新的集合(即这两个集合的并集)。

  假定这个操作之前两个集合是不相交的，然后选出一个代表。

• 查找 Find-Set(x)

  返回一个指针，指针包含x的(唯一)集合代表。

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=10010;
int fa[N];
inline int read()
{
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
	return s*w;
}
inline int mfind(int x)
{
	while(x!=fa[x]) x=fa[x]=fa[fa[x]];
	return x;//返回祖宗节点的值 
}
int main()
{
	int n=read(),m=read();
	for(int i=1;i<=n;++i)
		fa[i]=i;
	while(m--)
	{
		int z=read();
		int x=read();
		int y=read();
		int a=mfind(x),b=mfind(y);
		if(z==1)
		{
			fa[a]=b;
		}
		if(z==2)
		{
			if(a==b)
				puts("Y");
			else
				puts("N");
		}
	}
	return 0;
}

并查集查找部分代码优化版：

int get(int x)    //查询 
{
	if(x==fa[x]) return x;
	fa[x]=get(fa[x]);
	return fa[x]; 
}

并查集的应用

简单应用：统计一个无向图中连通子图的个数。

并查集实现

• 用有根树表示集合
• 树中的每个节点都表示一个集合的一个成员
• 每棵树表示一个集合
• 每个成员仅指向其父节点
• 每棵树的根表示代表，且它是它自己的父节点

时间复杂度

如果不优化，就在链的情况下，复杂度为O(n)

优化方法

按秩合并？ —目的是使包含较少节点的树的根指向包含较多节点的树的根。

目的是使包含较少节点的树的根指向包含较多节点的树的根。我们并不记录以每个节点为根的子树的大小。采用一种简化分析的方法。对每个节点，用秩 (rank) 表示节点高度的一个上界。在按秩合并中，具有较小秩的根在 Union 操作中要指向具有较大秩的根。

路径压缩（更常用的） 把每个节点的祖先直接指向根节点

例题1（POJ1182）

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。

现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这N个动物所构成的食物链关系进行描述：

第一种说法是"1 X Y"，表示X和Y是同类；

第二种说法是"2 X Y"，表示X吃Y。

此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

1） 当前的话与前面的某些真的话冲突，就是假话；

2） 当前的话中X或Y比N大，就是假话；

3） 当前的话表示X吃X，就是假话。

你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

思路：

有一种解法叫做带权并查集

如果x吃y，就连边权为1的边，如果xy为同类，就连边权为0的边；

对每个元素 x 建立 3 个元素， xa，xb，xc。
如果 x 吃 y，那么我们认为
xa 和 yb 在一个集合中（满足 A 吃 B）
xb 和 yc 在一个集合中（满足 B 吃 C）
xc 和 ya 在一个集合中（满足 C 吃 A）

同样的，如果 x 和 y 是同类那么我们认为
xa 和 ya 在一个集合中
xb 和 yb 在一个集合中
xc 和 yc 在一个集合中

初始的时候，建立大小为 3 * N 的并查集。

x 表示 xa， x + N 表示 xb，x + 2 * N 表示 xc。

如果碰到“1 x y”，说明 x 和 y 是同类

如果 x 和 y + N 在一个集合里，假话！

如果 x 和 y + 2 * N 在一个集合里，假话！

合并 x 和 y， x + N 和 y + N，x + 2 * N 和 y + 2 * N

代码：

#include<iostream>
#include<cstdio>
using namespace std;
int fa[150010],i1,i2,i3;
int x_self,x_eat,x_enemy;
int y_self,y_eat,y_enemy;
int get(int x)    //查询 
{
	if(x==fa[x]) return x;
	fa[x]=get(fa[x]);
	return fa[x]; 
}
void merge(int x,int y)   //合并 
{
	fa[get(x)]=get(y);
}
bool pd1()
{
	if(get(x_eat)==get(y_self))//如果输入的两个动物 我 吃 我 自 己
		return false;
	else
	{
		if(get(y_eat)==get(x_self))
			return false;
		else
			return true;
	}
}
bool pd2()
{
	if(get(x_self)==get(y_self))//如果输入的两个动物完全相同
		return false;
	else
	{
		if(get(y_eat)==get(x_self))
			return false;
	else
		return true;
	}
}
int main()
{
	int n,k,ou=0;
	cin>>n>>k;
	for(int i=1;i<=3*n;i++)
		fa[i]=i;
	for(int i=1;i<=k;i++)
	{
		cin>>i1>>i2>>i3;
		if(i3>n||i2>n)
		{
			ou++;
			continue;
		}//当所描述的动物>动物总数
		else
		{
			x_self=i2;
			x_eat=i2+n;
			x_enemy=i2+n*2;
			y_self=i3;
			y_eat=i3+n;
			y_enemy=i3+n*2;
			if(i1==1)
			{
				if(pd1())
				{//输入的两个动物不一样的地方分别讨论合并成为相同的
					if(get(x_self)!=get(y_self))
					  merge(x_self,y_self);
					if(get(x_eat)!=get(y_eat))
					  merge(x_eat,y_eat);
					if(get(x_enemy)!=get(y_enemy))
					  merge(x_enemy,y_enemy);
				}
				else//不要忘！
				ou++;
			}
			if(i1==2)
			{
				if(pd2())
				{
					if(get(x_eat)!=get(y_self))//X吃Y，即把X要吃的对象与Y自己合并
					  merge(x_eat,y_self);
					if(get(x_enemy)!=get(y_eat))//相反回来讨论x的敌人和y要吃的对象
					  merge(x_enemy,y_eat);
					if(get(x_self)!=get(y_enemy))
					  merge(x_self,y_enemy);
				}
				else//不要忘！
				ou++;
			}
		}
	}
	cout<<ou<<endl;
	return 0;
}

最小生成树

KRUSKAL

贪心地选择连接两个非联通图的最短的边

Kruskal 算法在每选择一条边加入到生成树集合 T 时，有两个关键步骤如下：

1. 从 E 中选择当前权值最小的边(u, v)

用最小堆或者按照边权大小排序实现

2. 选择权值最小的边后，要判断两个顶点是否属于同一个连通分量，如果是，要舍去；如果不是，要合并它们。

   用并查集实现

#include<iostream>
#include<cstdio>
using namespace std;
const int Maxn=100010;
const int Maxm=50050;
const int INF=0x99999;
int fa[Maxn],n,m,ans,cnt;
struct node{
	int v,u,w;
}e[Maxm<<2];
inline int read()
{
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
	return s*w;
}
inline int get(int x)
{
	while(x!=fa[x]) x=fa[x]=fa[fa[x]];
	return x;
}
inline bool cmp(node a,node b)
{
	return a.w<b.w;
}
inline void kruskal()
{
	sort(e+1,e+m+1,cmp);
	for(int i=1;i<=m;++i)
	{
		int eu=get(e[i].u);
		int ev=get(e[i].v);
		if(eu==ev)
			continue;
		ans+=e[i].w;
		fa[ev]=eu;
		if(++cnt==n-1) break;
	}
}
int main()
{
	n=read();m=read();
	for(int i=1;i<=n;++i)
		fa[i]=i;
	for(int i=1;i<=m;++i)
	{
		e[i].u=read();
		e[i].v=read();
		e[i].w=read();
	}
	kruskal();
	cout<<ans<<endl;
	return 0;
}

PRIM

每次贪心地选择已经遍历过的点权值最小的出边，访问这个边的另一个顶点（这个顶点不能在已有的集合中），再把这个点的出边都加到之前的集合中。

从连通无向图 G 中选择一个起始顶点 u0，首先将它加入到集合 T 中，然后选择与 u0 关联的、具有最小权值的边(u0, v)，将顶点 v 加入到顶点集合 T 中。

以后每一步都从 (u, v)（其中 u 在 T 中，v 在 T’中）找出权值最小的边，把顶点 v 加入到顶点集合 T 中。

重复第二步，直到图中的所有点都被加入 T 集合。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int Maxn=1000010;
const int Maxm=50050;
const int INF=0x999999;
int n,m,ans,now=1,tot,head[Maxn],dis[Maxn];
bool vis[Maxn];
struct node{
	int next;
	int v,w;
}e[Maxm<<1];
inline int read()
{
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
	return s*w;
}
inline void add(int v,int u,int w)
{
	e[++cnt].v=v;
	e[cnt].w=w;
	e[cnt].next=head[u];
	head[u]=cnt;
}
inline void init()
{
	n=read();m=read();
	for(int i=1;i<=m;++i)
	{
		int u,v,w;
		u=read();v=read();w=read();
		add(u,v,w);add(v,u,w);
	}
}
inline int prim()
{
	for(int i=2;i<=n;++i)
		dis[i]=INF;
	for(int i=head[1];i;e[i].next)
		dis[e[i].w]=min(e[i].w,dis[e[i].v])
	while(++tot<n)
	{
		int Minn=INF;
		vis[now]=1;
		for(int i=1;i<=n;++i)
			if(!vis[i]&&Minn>dis[i])
				Minn=dis[i],now=i;
		ans+=Minn;
		for(int i=head[now];i;i=e[i].next)
		{
			int v=e[i].v;
			if(!vis[v]&&dis[v]>e[i].w)
				dis[v]=e[i].w
		}
	}
	return ans;
}
int main()
{
	init();
	cout<<prim()<<endl;
	return 0;
}

例题 NOIP S 2013 D1T3

一个n个点m条边的图，每条边有边权。

q次询问，每次询问两点之间的路径上边权的最小值的最大值。

n < 10,000, m < 50,000, q < 30000

走他的最大生成树就好了

于是我们先用Kruskal算法在O(m log m)的时间复杂度下求出最大生成树，然后接下来的询问都在树上操作即可。

问题变成了：每查询树上一条路径的最小边权。

考虑倍增算法。我们不仅维护up[u][k]，还维护val[u][k]，表示从u开始往上爬2^k条边，遇到的最小值。

每次倍增向上跳的时候都记录下这次经过的最小值即可。这部分的时间复杂度是O((n + q) log n)。

至此问题完美解决。

最短路算法

最短路径问题 (Shortest Path Problem) 是有向图和无向图中的一个典型问题。

最短路问题要求解的是如果从图中某一顶点到达另一顶点的路径可能不止一条，如何找到这条路径，使得沿着这条路径各边上的权值总和（即从源点到终点的距离）达到最小，这条路径就称为最短路径。

根据边权的范围以及问题求解的需要，最短路问题可以分为以下 4 种情形，分别用不同的算法求解。

单源最短路径（固定一个顶点为原点，求源点到其他每个顶点的最短路径）

1. 边权非负：Dijkstra算法。

2. 边权允许为负：Bellman-Ford算法

3. Bellman-Ford算法的改进版本：SPFA算法

多源最短路径（计算每个点对之间的最短路）

4. 求所有顶点之间的最短路径：Floyd算法

多源最短路问题

FLOYED

for(int k=1;k<=n;++k)
	for(int i=1;i<=n;++i)
		for(int j=1;j<=n;++j)
			dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

把k放最外层的原因

单源最短路问题

DIJKSTRA

限定各边上的权值非负

1.设置两个顶点的集合 S 和 T

​ a)S 中存放已找到最短路径的顶点，初始时，集合 S 只有一个顶点， 即源点 v0.

​ b)T 中存放当前还未找到最短路径的顶点

2.在 T 集合中选取当前最短的一条最短路径 (v0, ..., vk)，从而将 vk 加入到顶点集合 S 中，并且修改源点 v0 到 T 中各顶点的最短路径长度

3.重复步骤 2，直到所有的顶点都被加入集合 S 中。

在 Dijkstra 算法中，最主要的工作是求源点到其他 n - 1 个顶点的最短路径及长度，要把其他 n - 1 个顶点加入到集合 S 中来。

每加入一个顶点，首先要在 n - 1 个顶点中判断每个顶点是否属于集合 T， 且最终要在 dist 数组中找元素值最小的顶点

然后要对其他 n - 1 个顶点，要判断每个顶点是否属于集合 T 以及是否需要修改 dist 数组元素值。

回顾一下在 Dijkstra 算法里，重复做以下 3 步工作：

​ 1.在数组 dist[i] 里查找 S[i] != 1，并且 dist[i] 最小的顶点 u。

​ 2.将 S[u] 改为 1，表示顶点 u 已经加入进来了。

​ 3.修改 T 集合中每个顶点 vk 的 dist 及 path 数组值。

第三步，不变。注意更新 dist 时，需要把新的 dist 插入堆，一次需要O(log n)。注意到每个点只会被选入 S 一次，每次会更新这个点所有的出边。因此每一条边只会被更新一次。m 条边总共产生的时间复杂度是O(m log n).

所以时间复杂度为(O(n^2))

查分约束

回顾一下单源最短路问题中的三角形不等式。
d[v] <= d[u] + edge[u] [v]
这是显然的，否则 d[v] 可以用 d[u] + edge[u] [v] 更新。
把 d[u] 移到左边： d[v] - d[u] <= edge[u] [v]
正好符合差分约束系统的格式！
一个差分约束系统就对应着一张有向图！

拓扑排序

拓扑排序其实非常简单

拓扑图：有向无环图

可以把拓扑排序看成是工厂生产的流程图，那么正确的生产流程就是拓扑排序

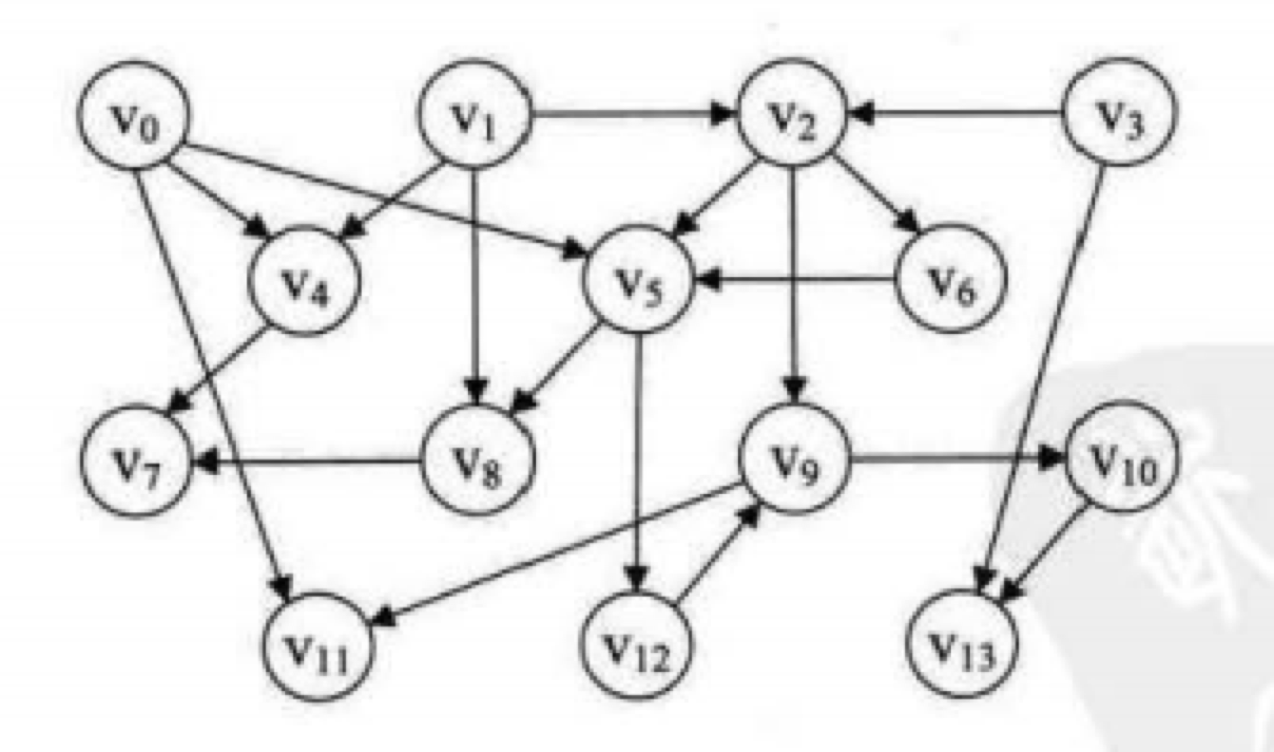
1.找没有出边的点，输出这个点，删除这个点，再找下一个没有出边的点

2.重复1

树上倍增

给定 n 个整数闭区间 [a[i], b[i]] 和 n 个整数 c[1], c[2], …, c[n]。编程实现以下 3 点：
读入闭区间的个数，每个区间的端点和整数 c[1], c[2], …, c[n]。
求一个最小的整数集合 Z，满足 |Z ∩ [a[i], b[i]]| >= c[i]，即 Z 里面的数中，范围在区间 [a[i], b[i]] 的个数不小于 c[i] 个。
输出答案。
n <= 50000 , 0 <= a[i] <= b[i] <= 50000.

该题目可建模成一个差分约束系统。
设 S[i] 是集合 Z 中小于等于 i 的元素个数。
Z 集合中范围在 [a[i], b[i]] 的整数个数即 S[b[i]] - S[a[i] - 1] 至少为 c[i]。
约束条件 1:
S[b[i]] - S[a[i] - 1] >= c[i] --> S[a[i] - 1] - S[b[i]] <= -c[i]
S[2] - S[7] <= -3
S[7] - S[10] <= -3
S[5] - S[8] <= -1
S[0] - S[3] <= -1
S[9] - S[11] <= -1

根据实际情况，还有两个约束条件
S[i] - S[i - 1] <= 1
S[i] - S[i - 1] >= 0
要么选要么不选
最终要求的是什么呢？
设所有区间中右端点的最大值为 mx，如样例中 mx = 11
设所有区间中左端点的最小值为 mn，如样例中 mn = 1
要求的是 S[mx] - S[mn - 1] 的最小值。
S[11] - S[0] >= M --> S[0] - S[11] <= -M
即求 11 到 0 的最短路径的长度，长度为 -M

但是考虑到后两个约束条件对应的不等式有 2 * (mx - mn + 1) 个。
再加上约束条件 1，构造的边数最多会达到 3 * 50000 条。
会超时！

优化

先用约束条件 1 构造有向图。
源点到各点最短距离初始为 0，因为 S[i] - S[mx] <= 0.
所以源点到各点的最短距离肯定是小于 0 的。
然后直接用 Bellman-Ford 算法求源点到各顶点的最短距离。
在每次循环中，约束条件1 判断完后，再判断后两个约束条件。

约束条件 2 的判断：
S[i] <= S[i - 1] + 1 --> S[i] - S[mx] <= S[i - 1] - S[mx] + 1
如果发现 dist[i] > dist[i - 1] + 1，那么把 dist[i] 修改为 dist[i - 1] + 1.
约束条件 3 的判断：
S[i - 1] <= S[i] --> S[i - 1] - S[mx] <= S[i] - S[mx]
如果 dist[i - 1] > dist[i]，那么把 dist[i - 1] 修改为 dist[i].

最后一个优化就是：如果在某一次执行完 Bellman-Ford 算法中的循环后， dist数组每个元素的值都没有发生变化，后续的循环就不用进行下去了。

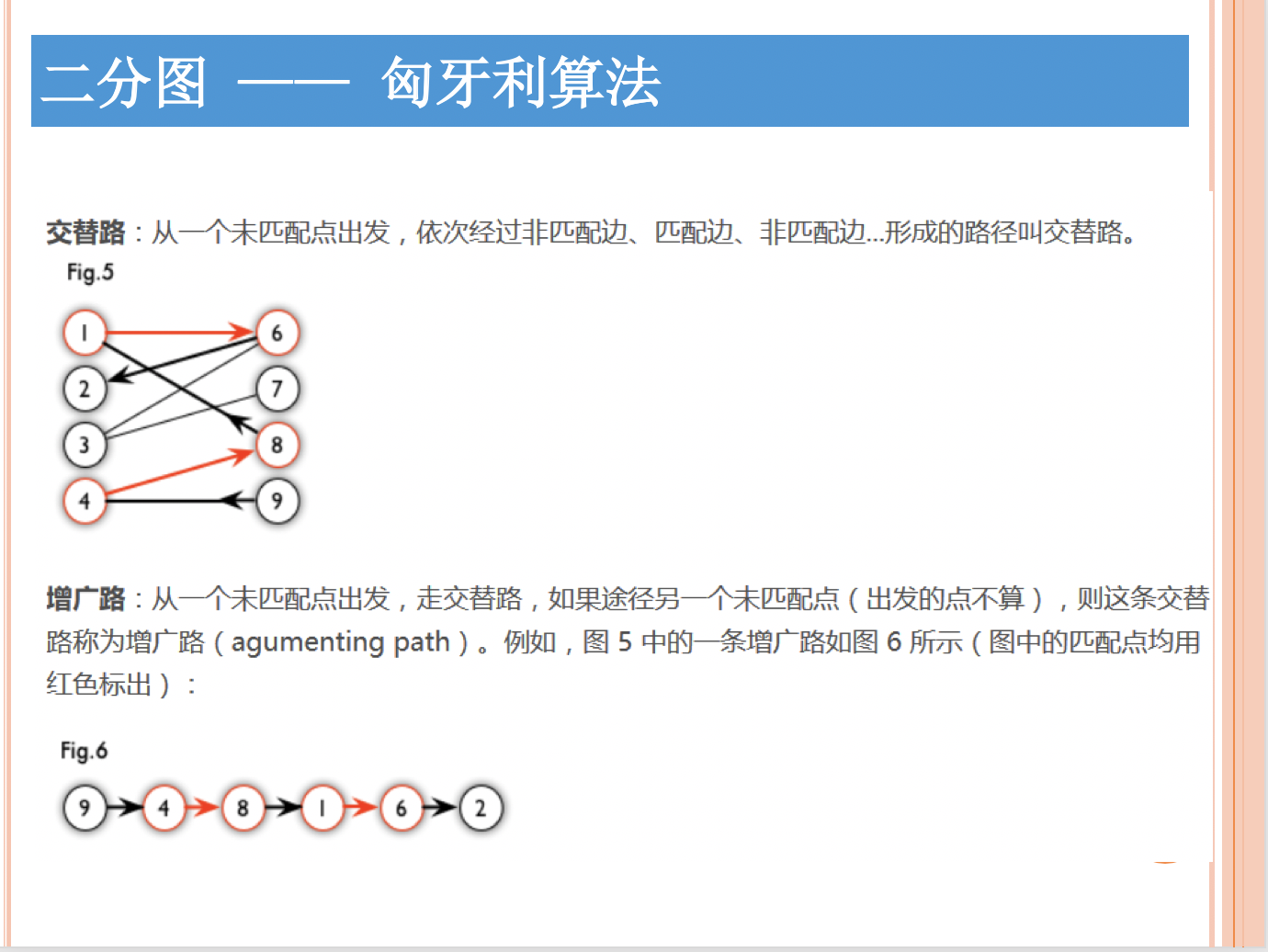
二分图

描述

简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集 和，使得每一条边都分别连接两个集合中的顶点。

如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。

染色问题适合求解

例1：现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

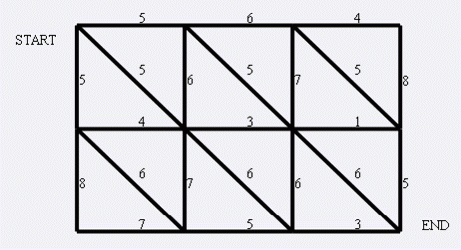
左上角点为 (1,1)(1,1)(1,1), 右下角点为 (N,M)(N,M)(N,M) (上图中 N=3N=3N=3, M=4M=4M=4).有以下三种类型的道路:

1. [1. (x,y)⇌(x+1,y)(x,y) ightleftharpoons(x+1,y)(*x*,*y*)⇌(*x*+1,*y*) ]
   [2. (x,y)⇌(x,y+1)(x,y) ightleftharpoons(x,y+1)(*x*,*y*)⇌(*x*,*y*+1) ]
   [3. (x,y)⇌(x+1,y+1)(x,y) ightleftharpoons(x+1,y+1)(*x*,*y*)⇌(*x*+1,*y*+1) ]

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的。左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角 (1,1)(1,1)(1,1) 的窝里，现在它们要跑到右下角 (N,M)(N,M)(N,M) 的窝中去，狼王开始伏击这些兔子。当然为了保险起见，如果一条道路上最多通过的兔子数为 KKK，狼王需要安排同样数量的 KKK 只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

分析：重新建图

从左下角到右上角建图。

通过切图片中三角形的方式从左下角进入，右上角退出，求所有路的最短路。

例2：有一张n个点m条边的无向图，其中有s个点上有加油站，有q次询问Q(a,b,c)，问能否开一辆邮箱容积为c的车从a到b(a，b均为加油站)。

分析：

找加油站的势力范围，

走的过程不是光走最短路径，而是在途中去最近势力范围的加油站加油。

1.求出每一个点离自己最近的加油站是谁。

2.假定一个超级元S，到所有点的距离为0。方便理解，为解释多源最短路

​ ①每个点离自己最近的加油站是谁。

​ ②这个加油站离自己有多远。

3.连一条长度为最小距离的边。

4.则这些边构成了所有加油站的距离。

5.最终去做最小生成树。

6.再判定他路径上的最大值有没有超过油量。

我们可以先求出离每个点ii最近的加油站w[i]w[i]和距离d[j]d[j],

然后对于原图中的每条边xx,yy,

如果w[x]!=w[y]w[x]!=w[y],就把w[x],w[y]w[x],w[y]连一条边,

距离就是d[x]+d[y]+w**x,yd[x]+d[y]+wx,y.

而w[i],d[i]w[i],d[i]怎么求呢?

跑多源SPFA就行了.

SPFA算法-Bellman-Ford堆优化

采用递推的方式计算 dist^k[u]
假设当前已经知道了 dist^k-1[u]
枚举 j，dist^k[u] = min{dist^k-1[u], dist^k-1[j] + edge[j] [u]}
这样就可以求出 dist^k-1[u]

初始状态 dist1[u] = edge[v0] [u].
这样就可以递推了。

SPFA更新原理

###### 		每个顶点的最短距离不会更新次数太多

用SPFA可以处理负权值的图。

在 SPFA 中，如果一个顶点入队列的次数超过 n，则表示有向图中存在负权值回路。
原理是：如果存在负权值回路，那么从源点到某个顶点的最短路径可以无限缩短，某些顶点入队列将超过 n 次。
因此，只需在 SPFA 算法中统计每个顶点入队列的次数，在取出队头顶点的时候，都判断其入队次数是否已经超过 n 次。

差分约束系统

差分约束系统的不等式组要么无解，要么有无数组解。

d[v] <= d[u] + edge[u] [v]
这是显然的，否则 d[v] 可以用 d[u] + edge[u] [v] 更新。
把 d[u] 移到左边： d[v] - d[u] <= edge[u] [v]
正好符合差分约束系统的格式！
一个差分约束系统就对应着一张有向图！

例1：陆逊派了很多密探，获得了他的敌人——刘备军队的信息。通过密探，他知道刘备的军队已经分成几十个大营，这些大营连成一片（一字排开），从左到右用 1，2，…，n 编号。
第 i 个大营最多能容纳 C[i] 个士兵。而且通过观察刘备军队的动静，陆逊可以估计到从第 i 个大营到第 j 个大营至少有多少士兵。
现在希望你估计出刘备最少有多少士兵。

n <= 1000, m <= 10000。

样例： （输出 1300）
3 2
1000 2000 1000
1 2 1100
2 3 1300

分析：

1.构造不等式：

每个兵营的实际人数也不能超过容量：
A[1] <= 1000 --> S[1] - S[0] <= 1000
A[2] <= 2000 --> S[2] - S[1] <= 2000
A[3] <= 1000 --> S[3] - S[2] <= 1000

s[i]-s[i-1]<=c[i];

每个兵营的实际人数要非负：
A[1] >= 0 --> S[1] - S[0] >= 0
A[2] >= 0 --> S[2] - S[1] >= 0
A[3] >= 0 --> S[3] - S[2] >= 0

s[i]-s[i-1]>=0;

把不等式全部转化为 S[i] - S[j] <= c 的形式
然后由 j 往 i 连一条有向边，权值为 c

S[0] - S[2] <= -1100
S[1] - S[3] <= -1300
S[2] - S[0] <= 3000
S[3] - S[1] <= 3000
S[1] - S[0] <= 1000
S[2] - S[1] <= 2000
S[3] - S[2] <= 1000
S[0] - S[1] <= 0
S[1] - S[2] <= 0
S[2] - S[3] <= 0

构造好网络之后，要求的是 S[3] - S[0] 的最小值，即 S[3] - S[0] >= M
M 要取最大值，S[0] - S[3] <= -M
即求 3 到 0 的最短路径，长度为 -M

求完再取反；

别忘了用SPFA检测是否存在负环。

总结

• 边权没有负权的时候一般使用d j k s t r a，有负权要使用S P F A；

• 用差分约束系统的时候一般使用前缀和列不等式；

例3：Frank是一个思想有些保守的高中老师。他决定下列任意两个学生至少要满足下面四条中的任意一条：

1.身高相差大于40cm；

2.性别相同；

3.喜欢的音乐属于不同类型；

4.喜欢的体育比赛相同；

任务是帮Frank找尽量多的学生，使得任意两个学生至少满足以上两条中的任意一条。

分析：

性别只有男女两种，所以可以化为二分图问题。

[二分图的最大点独集=点数-最大匹配数 ]

[二分图最大点覆盖集 = 二分图最大匹配数 ]

题外话：

​ 可以用多项式解决的问题叫做p的问题。

​ 即为没有只有两种情况的条件。

​ 复杂度为多项式的成为多项式时间。

​ np问题，用多项时间判断这个解是多少。

​ np完全问题，目前还没有非暴力解法。

例4：你在一座城市里负责一个大型活动的接待工作。明天将有m位客人从城市的不同位置出发，到达他们各自的目的地。已知每个人出发的时间，出发地点和目的地。你的任务市用尽量少的出租车送他们，使得每次出租车接客人时，至少能提前一分钟到达他们的位置。注意，为了满足这一条件，要么这位客人是这辆出租车接送的第一个人，要么在接送完上一个 客人后，有足够的时间从上一个目的地开到这里。

为了简单起见，假定区域是网格型的，地址用(x,y)表示，出租车从(x1,y1)到(x2,y2)处需要行驶|x1-x2|+|y1-y2|分钟。

分析 ：

有向无环图的最大匹配数

转换为二分图求解，求出最大匹配数。

最终的答案就是相减。

例5：有一张只有黑色和白色的无限连同图，求边长恰好为白边数恰好为need的的最小生成树。

思路：给所有白边加一个全值的活动范围。通过白色边的权值来调整在最小生成树中的比例。

用二分的方式卡出最合适的解

题目中说到了：保证有解，所以出现上述情况时一定有黑边==白边的边权

所以可以放心二分。

例6：给定 n 个整数闭区间 [a[i], b[i]] 和 n 个整数 c[1], c[2], …, c[n]。编程实现以下 3 点：
读入闭区间的个数，每个区间的端点和整数 c[1], c[2], …, c[n]。
求一个最小的整数集合 Z，满足 |Z ∩ [a[i], b[i]]| >= c[i]，即 Z 里面的数中，范围在区间 [a[i], b[i]] 的个数不小于 c[i] 个。
输出答案。
n <= 50000 , 0 <= a[i] <= b[i] <= 50000.

思路：

构造差分序列

根据实际情况，还有两个约束条件
S[i] - S[i - 1] <= 1
S[i] - S[i - 1] >= 0

要么选要么不选

最终要求的是什么呢？

设所有区间中右端点的最大值为 mx，如样例中 mx = 11
设所有区间中左端点的最小值为 mn，如样例中 mn = 1

要求的是 S[mx] - S[mn - 1] 的最小值。
S[11] - S[0] >= M --> S[0] - S[11] <= -M
即求 11 到 0 的最短路径的长度，长度为 -M

优化

考虑到后两个约束条件对应的不等式有 2 * (mx - mn + 1) 个。
再加上约束条件 1，构造的边数最多会达到 3 * 50000 条。

会超时！

先用约束条件 1 构造有向图。
源点到各点最短距离初始为 0，因为 S[i] - S[mx] <= 0.
所以源点到各点的最短距离肯定是小于 0 的。
然后直接用 Bellman-Ford 算法求源点到各顶点的最短距离。

在每次循环中，约束条件1 判断完后，再判断后两个约束条件。

约束条件 2 的判断：
S[i] <= S[i - 1] + 1 --> S[i] - S[mx] <= S[i - 1] - S[mx] + 1
如果发现 dist[i] > dist[i - 1] + 1，那么把 dist[i] 修改为 dist[i - 1] + 1.

约束条件 3 的判断：
S[i - 1] <= S[i] --> S[i - 1] - S[mx] <= S[i] - S[mx]
如果 dist[i - 1] > dist[i]，那么 把 dist[i - 1] 修改为 dist[i].

例7：一张n点边的dag，问多少个点满足最多存在一个点不能够到它或它不能到

[n,m≤3×10^5 ]

思路：

暴力做法：dfs反向查找，看能否反向到达；

优化做法：拓扑排序。

比较没有入度的点：

​ 若没有入度的点的个数为1：则该点可以到达任意点，把该点删去。重复前面的过程。

​ 若没有入度的点的个数为2：则两点一定不可相互到达，个数加入答案。重复前面的过程。

​ 若没有入度的点的个数为3：则该三点一定不可相互到达，但不满足最多存在一点的条件，三个点同时删去。重复前面的过程。

​ 只剩最后一个点的时候加入答案。