无监督学习
通俗来讲,无监督学习就是没有目标值
无监督学习包含算法
- 聚类
- K-means(K均值聚类)
- 降维
- PCA
K-means原理
K-means的聚类效果图
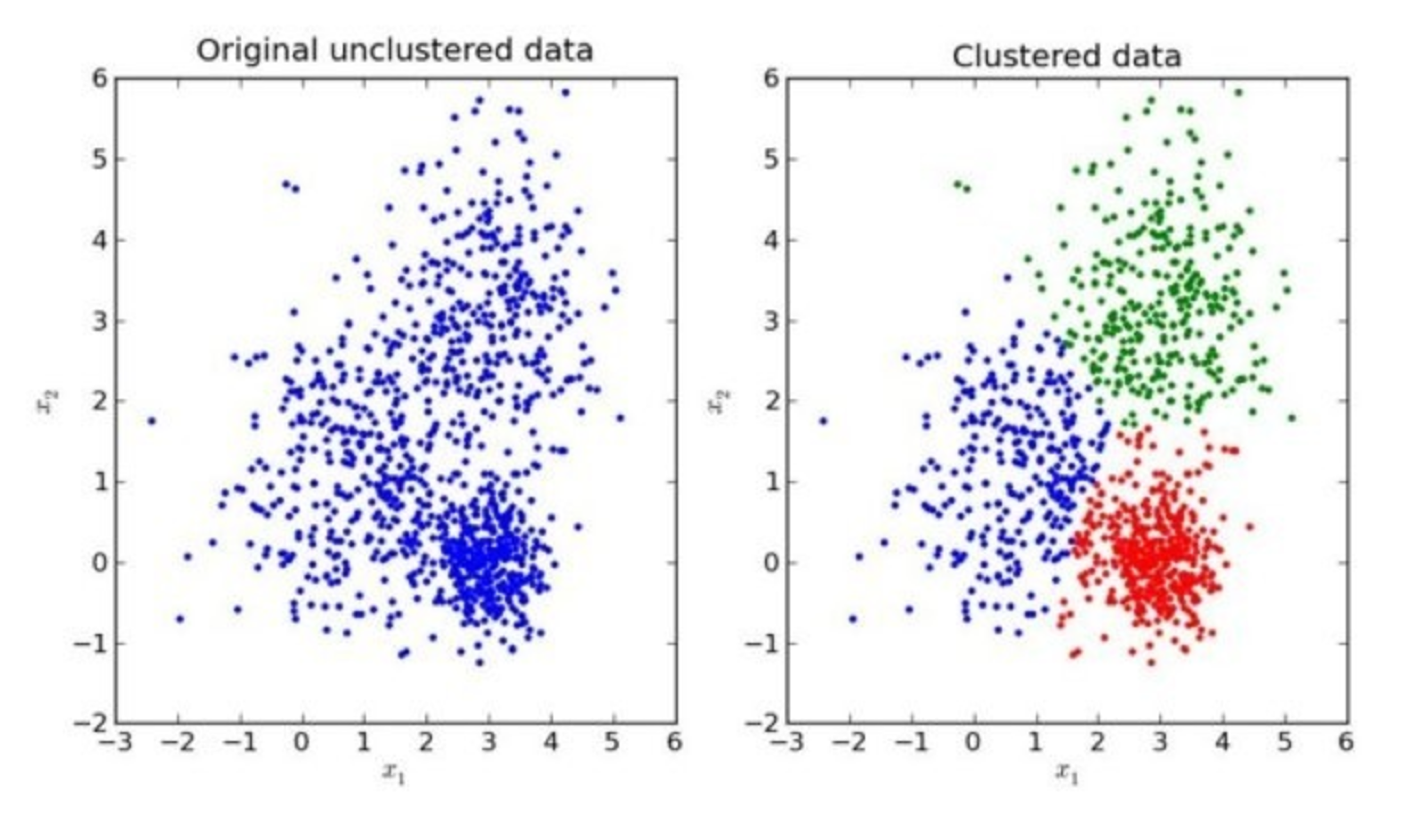
K-means聚类步骤
- 随机设置K个特征空间内的点作为初始的聚类中心
- 对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
- 接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
- 如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行第二步过程

K-meansAPI
sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
- k-means聚类
- n_clusters:开始的聚类中心数量
- init:初始化方法,默认为'k-means ++’
- labels_:默认标记的类型,可以和真实值比较(不是值比较)
案例:k-means对Instacart Market用户聚类
import pandas as pd from sklearn.decomposition import PCA from sklearn.cluster import KMeans # 1、获取数据集 # ·商品信息- products.csv: # Fields:product_id, product_name, aisle_id, department_id # ·订单与商品信息- order_products__prior.csv: # Fields:order_id, product_id, add_to_cart_order, reordered # ·用户的订单信息- orders.csv: # Fields:order_id, user_id,eval_set, order_number,order_dow, order_hour_of_day, days_since_prior_order # ·商品所属具体物品类别- aisles.csv: # Fields:aisle_id, aisle products = pd.read_csv("../dataset/products.csv") order_products = pd.read_csv("../dataset/order_products__prior.csv") orders = pd.read_csv("../dataset/orders.csv") aisles = pd.read_csv("../dataset/aisles.csv") # 2、合并表,将user_id和aisle放在一张表上 # 1)合并orders和order_products on=order_id tab1:order_id, product_id, user_id tab1 = pd.merge(orders, order_products, on=["order_id", "order_id"]) # 2)合并tab1和products on=product_id tab2:aisle_id tab2 = pd.merge(tab1, products, on=["product_id", "product_id"]) # 3)合并tab2和aisles on=aisle_id tab3:user_id, aisle tab3 = pd.merge(tab2, aisles, on=["aisle_id", "aisle_id"]) # 3、交叉表处理,把user_id和aisle进行分组 table = pd.crosstab(tab3["user_id"], tab3["aisle"]) # 4、主成分分析的方法进行降维 # 1)实例化一个转换器类PCA transfer = PCA(n_components=0.95) # 2)fit_transform data = transfer.fit_transform(table) data_new = data[:500] km = KMeans(n_clusters=3) km.fit(data_new) y_predict = km.predict(data_new) print(y_predict)

Kmeans性能评估指标
轮廓系数

注:对于每个点i 为已聚类数据中的样本 ,b_i 为i 到其它族群的所有样本的距离最小值,a_i 为i 到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值
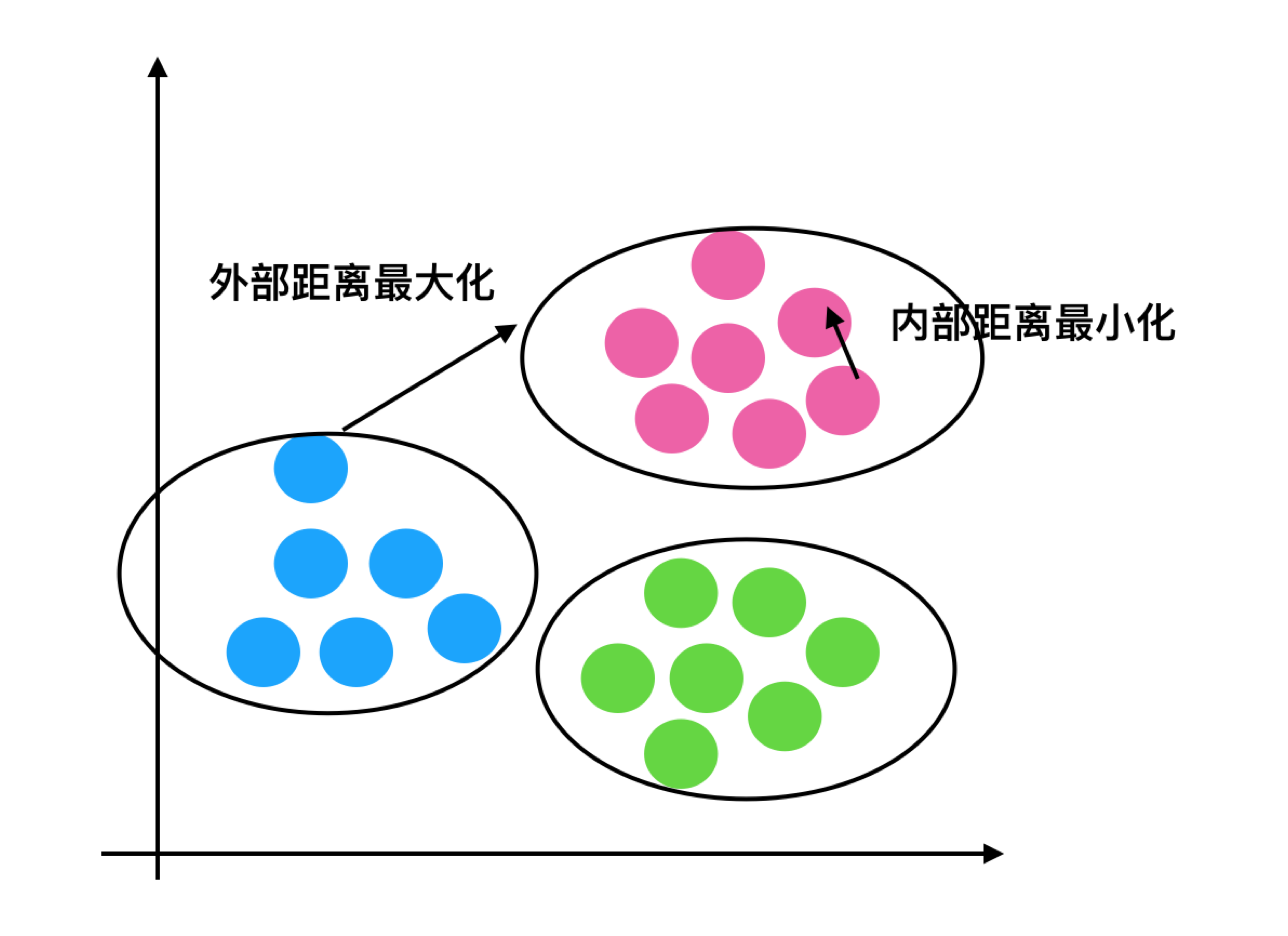
分析
-
1、计算出蓝1离本身族群所有点的距离的平均值a_i
-
2、蓝1到其它两个族群的距离计算出平均值红平均,绿平均,取最小的那个距离作为b_i
- 根据公式:极端值考虑:如果b_i >>a_i: 那么公式结果趋近于1;如果a_i>>>b_i: 那么公式结果趋近于-1
结论
如果b_i>>a_i:趋近于1效果越好, b_i<<a_i:趋近于-1,效果不好。轮廓系数的值是介于 [-1,1] ,越趋近于1代表内聚度和分离度都相对较优。
轮廓系数API
- sklearn.metrics.silhouette_score(X, labels)
- 计算所有样本的平均轮廓系数
- X:特征值
- labels:被聚类标记的目标值
silhouette_score(data_new, y_predict)

K-means总结
- 特点分析:采用迭代式算法,直观易懂并且非常实用
- 缺点:容易收敛到局部最优解(多次聚类)