分块算法实质上是一种是通过分成多块后在每块上打标记以实现快速区间修改,区间查询的一种算法。其均摊时间复杂度为 O(√ n)
分块算法相较于各种树形数据结构,具有简便易写,方便调试等多种优点。在同等数据规模下,如 1e5 ,其时间效率并不会低太多,在考试时反而是一种有力的得分方法。
但是若是数据量到1s/5e5以上,基本上就会T…
分块的实质
分块其实是一种树形结构,它是一种只有三层的树,形态如下:
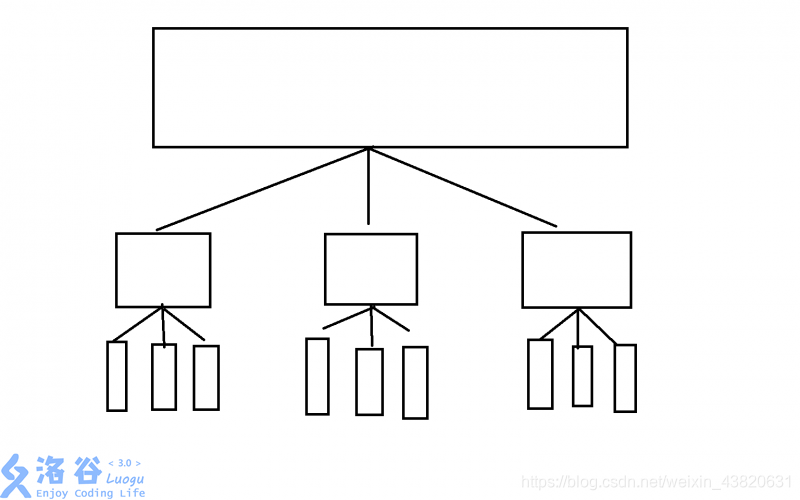
下面给出几种分块常用板子:
1.区间加法,单点查询
#include<bits/stdc++.h> using namespace std; #define maxn 500005 #define ll long long #define rint register int int n,m,blo; int v[maxn],bl[maxn],sum[maxn]; void add(int a,int b,int c){ for(rint i=a;i<=min(bl[a]*blo,b);i++) v[i]+=c; if(bl[a]!=bl[b]) for(rint i=(bl[b]-1)*blo+1;i<=b;i++) v[i]+=c; for(rint i=bl[a]+1;i<=bl[b]-1;i++) sum[i]+=c; } int main() { scanf("%d %d",&n,&m); blo=sqrt(n); for(int i=1;i<=n;i++) bl[i]=(i-1)/blo+1; for(int i=1;i<=n;i++) scanf("%d",&v[i]); while(m--){ int op,a,b,c; scanf("%d",&op); if(op==1){ scanf("%d %d %d",&a,&b,&c); add(a,b,c); } else{ scanf("%d",&a); printf("%d ",v[a]+sum[bl[a]]); } } return 0; }
这份代码能过5e5数据量的 洛谷P3368 【模板】树状数组 2…
2.区间加法,区间求和
#include<bits/stdc++.h> using namespace std; #define maxn 300005 #define ll long long int n,m,blo; int v[maxn],bl[maxn],atag[maxn]; ll sum[maxn]; void add(int a,int b,int c){ for(int i=a;i<=min(bl[a]*blo,b);i++){ v[i]+=c; sum[bl[a]]+=c; } if(bl[a]!=bl[b]) for(int i=(bl[b]-1)*blo+1;i<=b;i++){ v[i]+=c; sum[bl[b]]+=c; } for(int i=bl[a]+1;i<=bl[b]-1;i++) atag[i]+=c; } ll getsum(int a,int b){ ll ans=0; for(int i=a;i<=min(bl[a]*blo,b);i++) ans+=v[i]+atag[bl[a]]; if(bl[a]!=bl[b]) for(int i=(bl[b]-1)*blo+1;i<=b;i++) ans+=v[i]+atag[bl[b]]; for(int i=bl[a]+1;i<=bl[b]-1;i++) ans+=sum[i]+atag[i]*blo; return ans; } int main() { scanf("%d %d",&n,&m); blo=sqrt(n); for(int i=1;i<=n;i++) scanf("%d",&v[i]); for(int i=1;i<=n;i++){ bl[i]=(i-1)/blo+1; sum[bl[i]]+=v[i]; } while(m--){ int op,a,b,c; scanf("%d",&op); if(op==1){ scanf("%d %d %d",&a,&b,&c); add(a,b,c); } else{ scanf("%d %d",&a,&b); printf("%lld ",getsum(a,b)); } } return 0; }
3.区间加法,区间查小于X的个数
#include<bits/stdc++.h> using namespace std; #define maxn 300005 #define ll long long int n,m,blo; int v[maxn],bl[maxn],atag[maxn]; vector<int>ve[505]; void reset(int x) { ve[x].clear(); for(int i=(x-1)*blo+1;i<=min(x*blo,n);i++) ve[x].push_back(v[i]); sort(ve[x].begin(),ve[x].end()); } void add(int a,int b,int c) { for(int i=a;i<=min(bl[a]*blo,b);i++) v[i]+=c; reset(bl[a]); if(bl[a]!=bl[b]){ for(int i=(bl[b]-1)*blo+1;i<=b;i++) v[i]+=c; reset(bl[b]); } for(int i=bl[a]+1;i<=bl[b]-1;i++) atag[i]+=c; } int query(int a,int b,int c) { int ans=0; for(int i=a;i<=min(bl[a]*blo,b);i++) if(v[i]+atag[bl[a]]<c)ans++; if(bl[a]!=bl[b]) for(int i=(bl[b]-1)*blo+1;i<=b;i++) if(v[i]+atag[bl[b]]<c)ans++; for(int i=bl[a]+1;i<=bl[b]-1;i++) { int x=c-atag[i]; ans+=lower_bound(ve[i].begin(),ve[i].end(),x)-ve[i].begin(); } return ans; } int main() { scanf("%d %d",&n,&m); blo=sqrt(n); for(int i=1;i<=n;i++) scanf("%d",&v[i]); for(int i=1;i<=n;i++) { bl[i]=(i-1)/blo+1; ve[bl[i]].push_back(v[i]); } for(int i=1;i<=bl[n];i++) sort(ve[i].begin(),ve[i].end()); for(int i=1;i<=m;i++) { int f,a,b,c; scanf("%d %d %d %d",&f,&a,&b,&c); if(f==0)add(a,b,c); if(f==1)printf("%d ",query(a,b,c)); } return 0; } /* 6 5 1 5 6 4 2 3 0 1 4 3 1 1 6 4 0 1 2 1 1 1 6 9 1 5 6 1 */
4.区间加乘,单点查值
#include<bits/stdc++.h> using namespace std; #define maxn 300005 #define ll long long int n,m,blo; int v[maxn],bl[maxn],atag[maxn],mtag[maxn]; void add(int a,int b,int c) { for(int i=a;i<=min(bl[a]*blo,b);i++) v[i]+=c; if(bl[a]!=bl[b]) for(int i=(bl[b]-1)*blo+1;i<=b;i++) v[i]+=c; for(int i=bl[a]+1;i<=bl[b]-1;i++) atag[i]+=c; } void muti(int a,int b,int c) { for(int i=a;i<=min(bl[a]*blo,b);i++) v[i]*=c; atag[bl[a]]*=c; if(bl[a]!=bl[b]){ for(int i=(bl[b]-1)*blo+1;i<=b;i++) v[i]*=c; atag[bl[b]]*=c; } for(int i=bl[a]+1;i<=bl[b]-1;i++){ atag[i]*=c; mtag[i]*=c; } } int main() { scanf("%d %d",&n,&m); blo=sqrt(n); for(int i=1;i<=n;i++) scanf("%d",&v[i]); for(int i=1;i<=n;i++) bl[i]=(i-1)/blo+1; for(int i=1;i<=sqrt(n)+1;i++) mtag[i]=1; while(m--){ int op,a,b,c; scanf("%d",&op); if(op==1){ scanf("%d %d %d",&a,&b,&c); add(a,b,c); } if(op==2){ scanf("%d %d %d",&a,&b,&c); muti(a,b,c); } if(op==3){ scanf("%d",&a); printf("%lld ",1ll*v[a]*mtag[bl[a]]+atag[bl[a]]); } } }
5.区间异或,区间求值
#include<bits/stdc++.h> using namespace std; #define maxn 300005 #define ll long long int n,m,blo; int v[maxn],bl[maxn],t[maxn]; ll atag[maxn]; void chang(int a,int b){ for(int i=a;i<=min(bl[a]*blo,b);i++){ atag[bl[a]]-=(v[i]^t[bl[a]]); v[i]^=1; atag[bl[a]]+=(v[i]^t[bl[a]]); } if(bl[a]!=bl[b]) for(int i=(bl[b]-1)*blo+1;i<=b;i++){ atag[bl[b]]-=(v[i]^t[bl[b]]); v[i]^=1; atag[bl[b]]+=(v[i]^t[bl[b]]); } for(int i=bl[a]+1;i<=bl[b]-1;i++){ atag[i]=blo-atag[i]; t[i]^=1; } } ll query(int a,int b){ int ans=0; for(int i=a;i<=min(bl[a]*blo,b);i++) ans+=1ll*v[i]^t[bl[a]]; if(bl[a]!=bl[b]) for(int i=(bl[b]-1)*blo+1;i<=b;i++) ans+=1ll*v[i]^t[bl[b]]; for(int i=bl[a]+1;i<=bl[b]-1;i++) ans+=1ll*atag[i]; return ans; } int main() { scanf("%d %d",&n,&m); blo=sqrt(n); for(int i=1;i<=n;i++) bl[i]=(i-1)/blo+1; while(m--){ int op,a,b; scanf("%d %d %d",&op,&a,&b); if(op==0)chang(a,b); else printf("%lld ",query(a,b)); } return 0; }