本文转自公众号---遇见数学---图解数学---线性代数部分
感谢遇见数学工作组将大学课本晦涩难懂、故作高深的数学知识,用通俗易懂而又生动有趣的方法解释出来。
线性变换是线性空间中的运动, 而矩阵就是用来描述这种变换的工具. 这样说还是没有直观印象, 所以还是直接看图解的动画吧.
矩阵不仅仅只是数值的表:
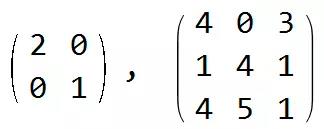
其实表示了在该矩阵的作用下, 线性空间是怎样的变化, 观察下图二维平面中水平和垂直方向的伸缩:
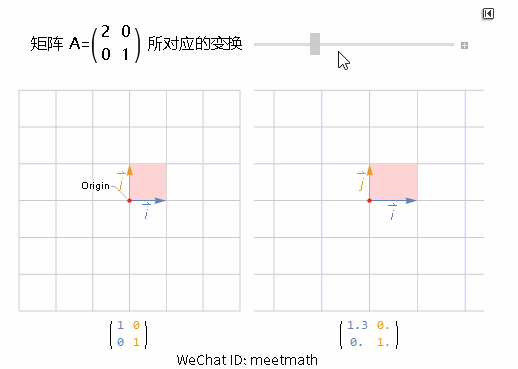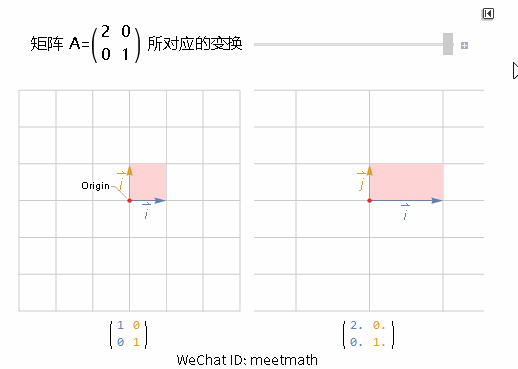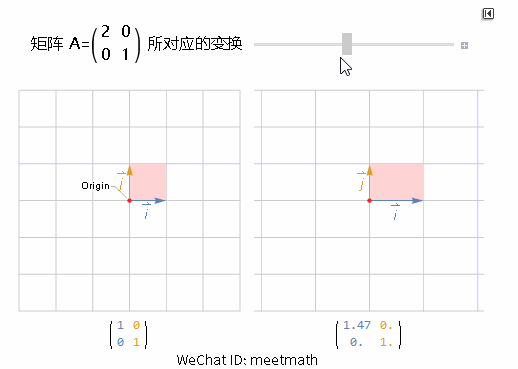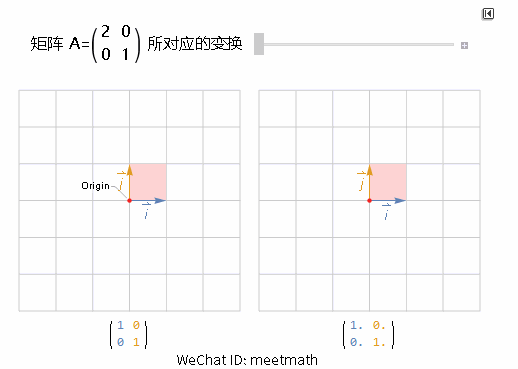
可以看到:
-
垂直方向并没有发生任何变换(A 的第二列没有变化);
-
水平方向伸展了 2 倍;
-
浅红色方格在变换后面积变成了原来的 2 倍,这里其实就是行列式的意义 - 面积的扩张倍率 Det(A)=2
再看到更多矩阵变换之前, 先停下来看看这个例子:
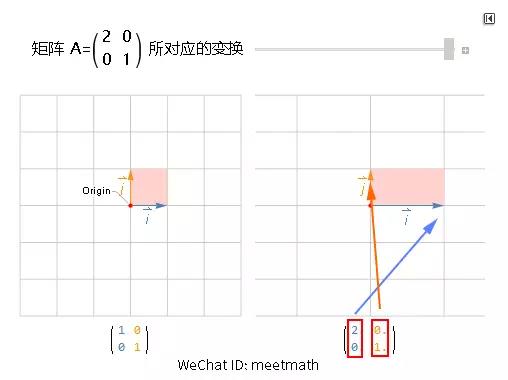
变换前矩阵的基底向量 i (1,0) 移动到了 (2,0) 的位置, 而 j 基底向量 (0,1) 还是 (0,1) 没发生任何变换(移动) - 也就是基底的变化:
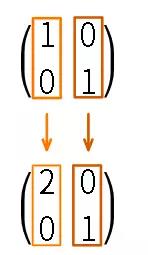
一旦明白了基底的变化, 那么整个线性变换也就清楚了 - 因为所有向量的变化都可以由改变后的基向量线性表出. 观察下面向量(1, 1.5) 和 (-1, -3) 变换后的位置:

向量 (1, 1.5) 在变换后的位置, 其实就是变换后基向量的线性表示, 也可以看到矩阵的乘法是如何计算的:
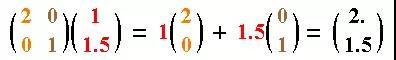
类似对于(-1, -3) 变换后的位置 , 也是一样的计算方法:
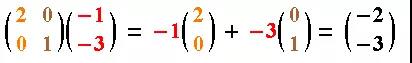
可以再次观察上图来体会, 验证算出的结果.
下面再看其他的变换矩阵, 这里矩阵 A 的对角线中有 0 元素:

可以看到:
-
水平方向变为 0 倍;
-
垂直方向被拉伸为 2 倍;
-
面积的变化率为 0 倍, 也就是 Det(A) = 0;
基底的变化如下:
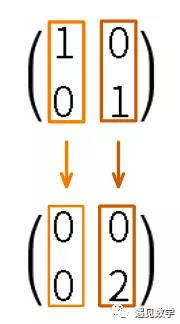
再看看下面矩阵 A 的变换:
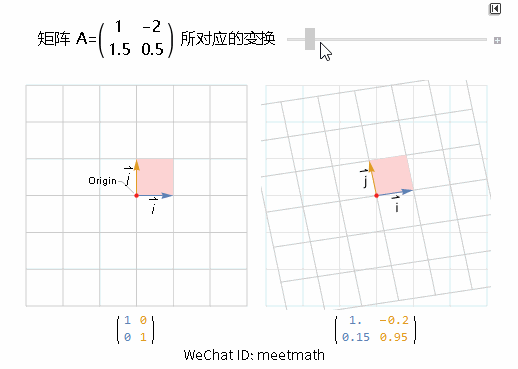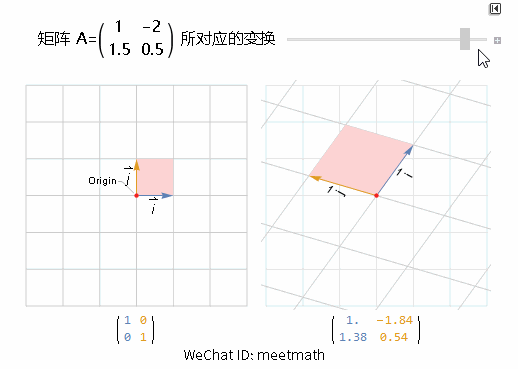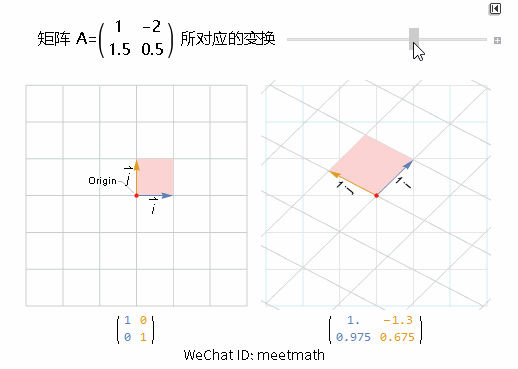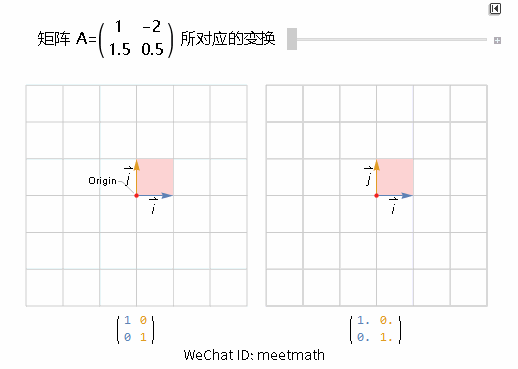
可以看到:
-
整个空间向左倾斜转动;
-
面积放大为原来的 Det(A) = 3.5 倍;
上面在 3 个不同的矩阵作用下(相乘), 整个空间发生不同的变换, 但是原点没有改变, 且直线依然还是直线, 平行的依然保持平行, 这就是线性变换的本质.
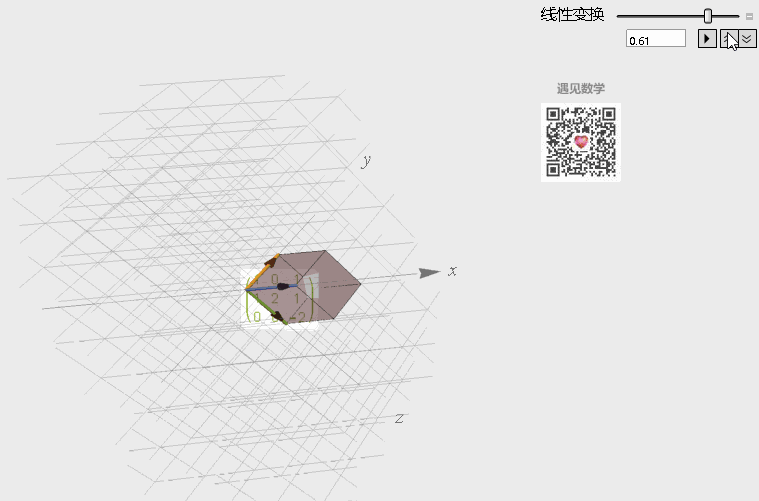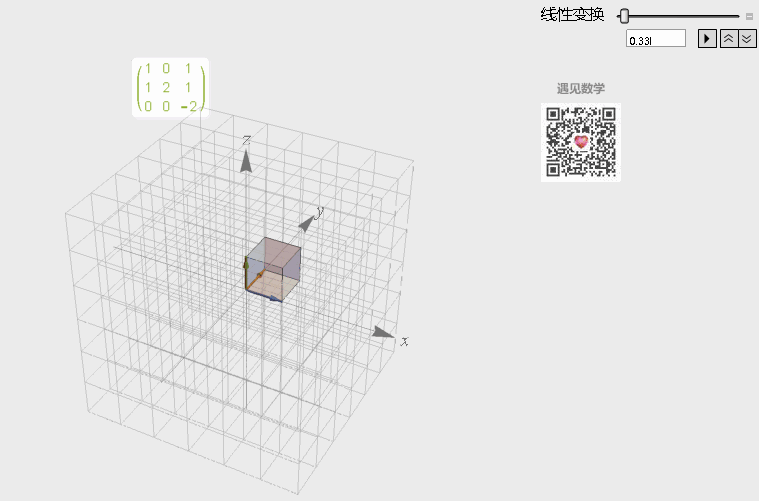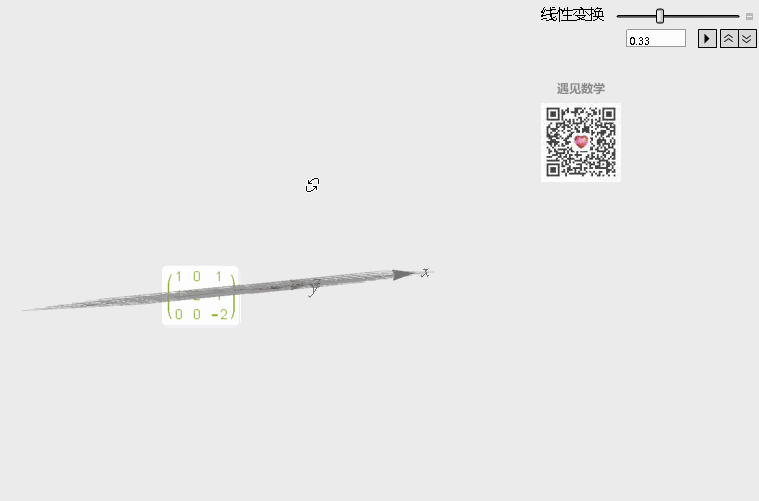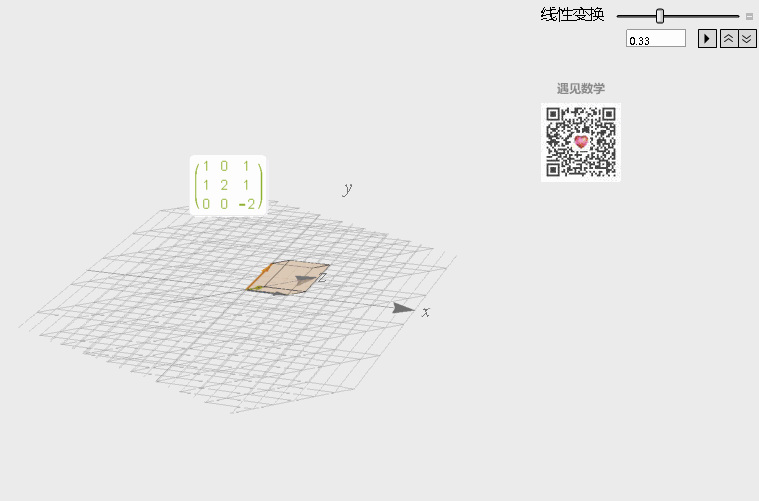
类似, 在三维线性空间内, 矩阵也用于这样的线性变换, 需要注意的是这里行列式可以看成经过变换后体积变化的倍率. 观察下图, 经过下面矩阵 A 的变换中, 空间会经过镜像翻转变换(扁平化为线), 所以行列式的值会是负数.