Codeforces Global Round 3

同样还是补题 老年人晚上熬不起夜（其实是那天去找女朋友玩了回来晚了

A. Another One Bites The Dust

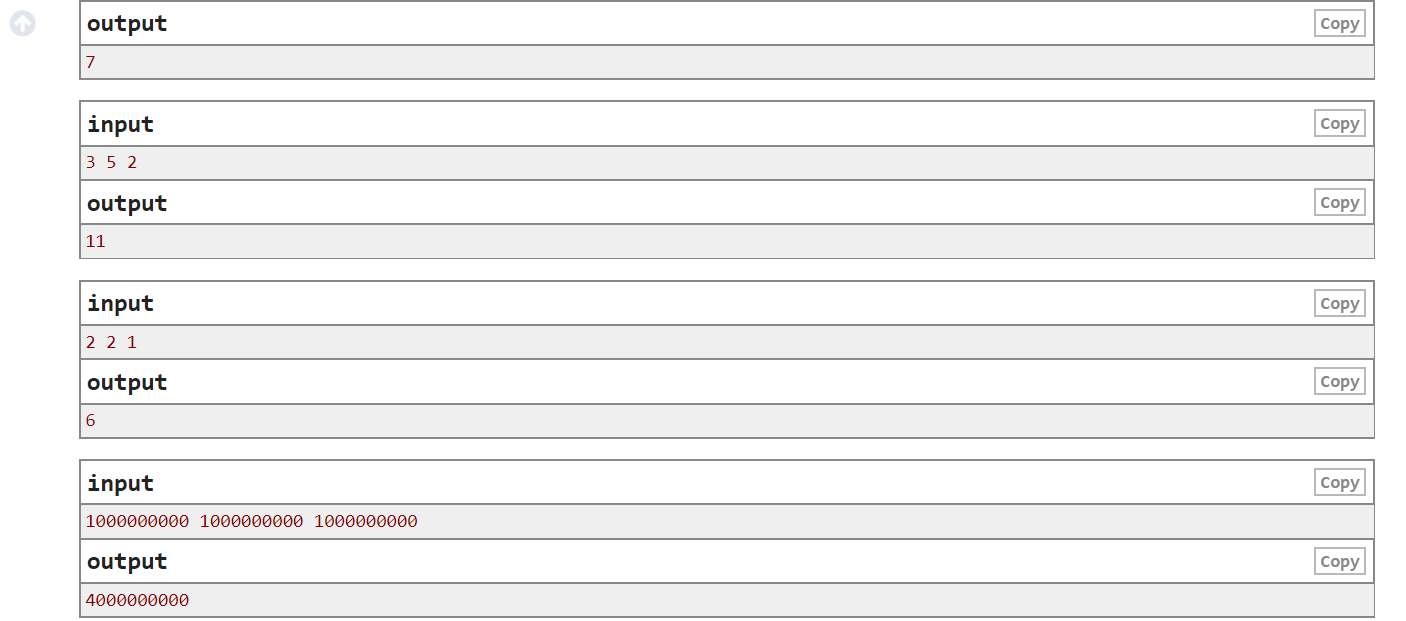
题意 给出a个"a" b个"b" c个"ab" 然后能组成如"ababa"形串的最大长度

水题 如果a == b的话 就刚好按若干个ab的顺序排 即最长长度为(a + c) * 2

a != b的话 也是按若干个ab排 但多出来的一个a可以排在最后一个b后面

同理 多出来的一个b可以排在最先一个a前面 即最长长度(min(a, b) + c) * 2 + 1

AC代码：

#include<bits/stdc++.h>
#define pi acos(-1)
typedef long long ll;
typedef unsigned long long ull;
using namespace std;

namespace io {
    const int SIZE = 1e7 + 10;
    char inbuff[SIZE];
    char *l, *r;
    inline void init() {
        l = inbuff;
        r = inbuff + fread(inbuff, 1, SIZE, stdin);
    }
    inline char gc() {
        if (l == r) init();
        return (l != r) ? *(l++) : EOF;
    }
    void read(int &x) {
        x = 0; char ch = gc();
        while(!isdigit(ch)) ch = gc();
        while(isdigit(ch)) x = x * 10 + ch - '0', ch = gc();
    }
} using io::read;

bool cmp(const int &a, const int &b){
    return a > b;
}

int main(){
    ll a, b, c;
    cin>>a>>b>>c;
    if (a == b) cout<<(a + c) * 2<<endl;
    else cout<<(min(a, b) + c) * 2 + 1<<endl;
    return 0;
}

B. Born This Way

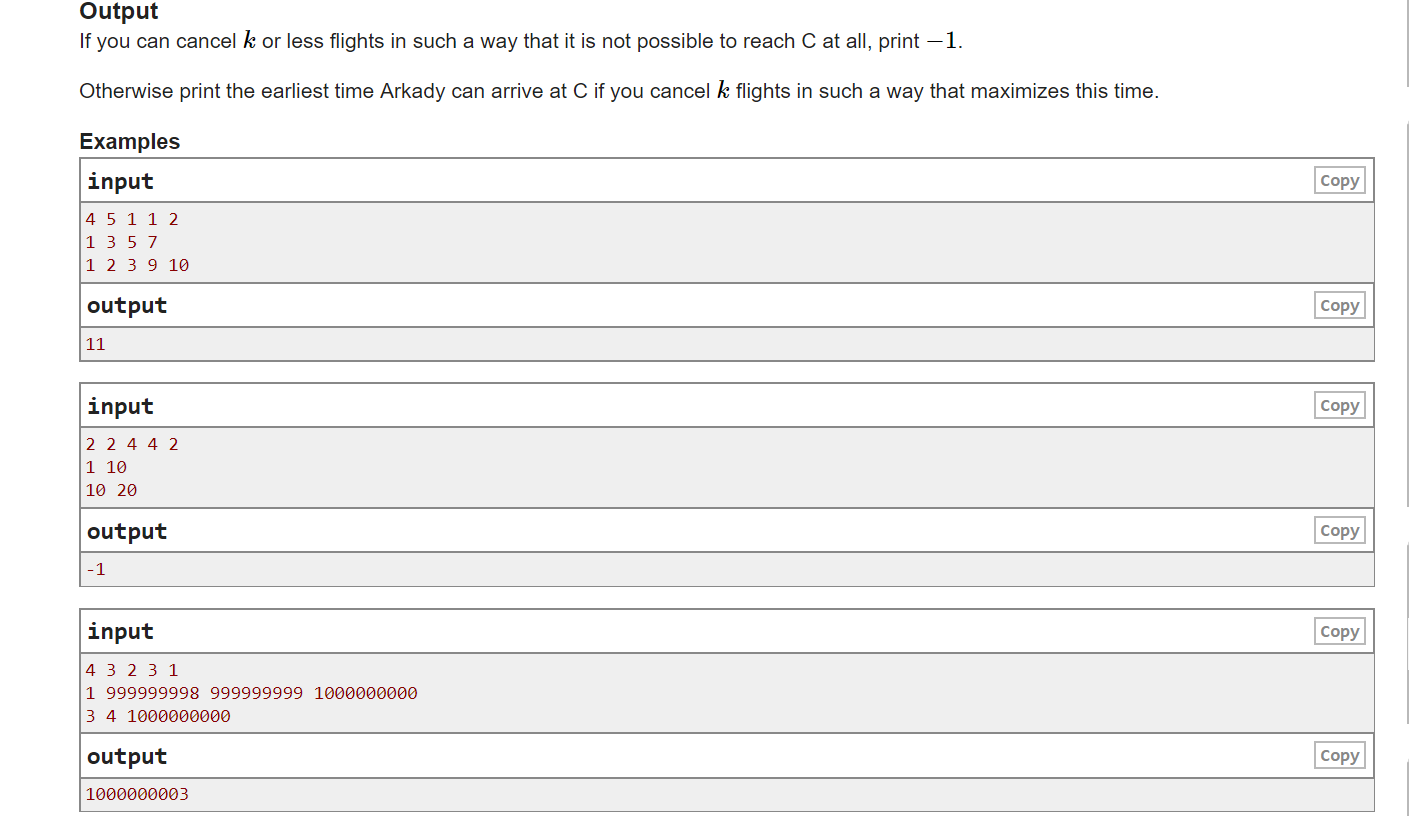
题意 某个人要买张从A到C的机票 但是上帝并不想让他这么顺利（瞎编的）

他只能从A飞到B 再从B飞到C

给出n趟从A到B的飞机起飞时刻与m趟从B到C的飞机起飞时刻还有A到B的飞机飞行时间ta和B到C的飞机飞行时间tb

你现在要千方百计让这个人最晚时间到达目的地 你能取消小于等于k趟航班

若取消后不能到达 输出-1 否则 输出最晚的时间

先直接把a数组都加上ta 再跟b数组的每一项比较 注意特判n <= k或m <= k时的情况

AC代码：

#include<bits/stdc++.h>
#define pi acos(-1)
typedef long long ll;
typedef unsigned long long ull;
using namespace std;

namespace io {
    const int SIZE = 1e7 + 10;
    char inbuff[SIZE];
    char *l, *r;
    inline void init() {
        l = inbuff;
        r = inbuff + fread(inbuff, 1, SIZE, stdin);
    }
    inline char gc() {
        if (l == r) init();
        return (l != r) ? *(l++) : EOF;
    }
    void read(int &x) {
        x = 0; char ch = gc();
        while(!isdigit(ch)) ch = gc();
        while(isdigit(ch)) x = x * 10 + ch - '0', ch = gc();
    }
} using io::read;

bool cmp(const int &a, const int &b){
    return a > b;
}

const int N = 2e5 + 5;
ll n, m, ta, tb, k;
ll a[N], b[N];
ll ans;

int main(){
    cin>>n>>m>>ta>>tb>>k;
    bool flag = true;
    for (int i = 1; i <= n; i++){
        cin>>a[i];
        a[i] += ta;
    }
    for (int i = 1; i <= m; i++) cin>>b[i];
    for (int i = 0; i <= k; i++){
        int t = lower_bound(b + 1, b + 1 + m, a[i + 1]) - b + k - i;
        if (t > m){
            flag = false;
            break;
        }
        ans = max(ans, b[t] + tb);
    }
    if (n <= k || m <= k) flag = false;
    if (flag) cout<<ans<<endl;
    else cout<<-1<<endl;
    return 0;
}